《機械》〈回転機〉[H29:問1] 突極形同期電動機の出力トルクに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，突極形同期電動機の出力トルクに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

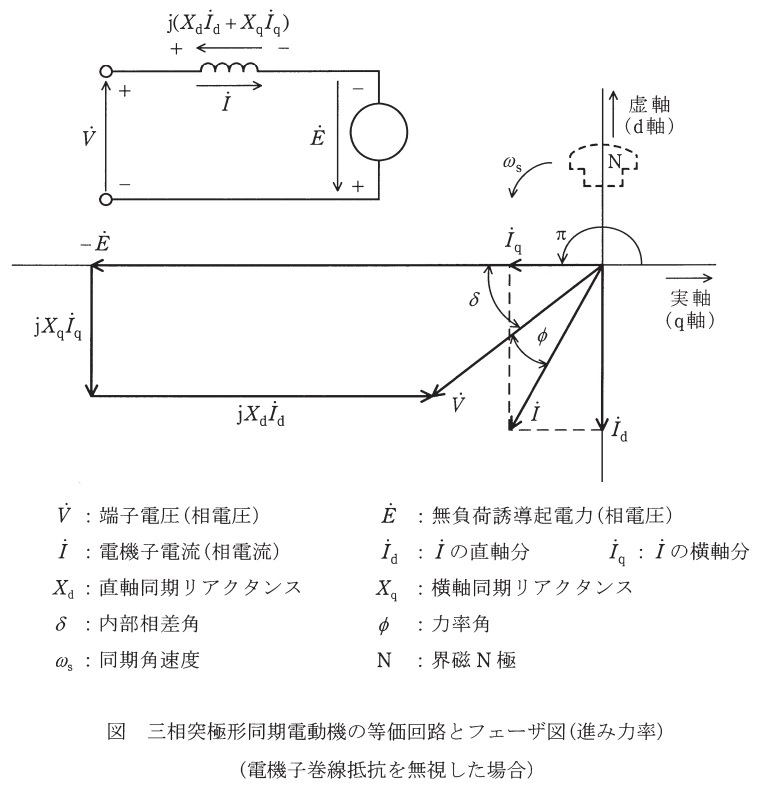
図は，三相突極形同期電動機の等価回路及びその等価回路に基づくフェーザ図(進み力率)を示している。フェーザ図において，界磁$ \ \mathrm{N} \ $極の中心線に一致している$ \ \mathrm{d} \ $軸に虚軸を，$ \ \mathrm{d} \ $軸より$ \ \mathrm{90°} \ $遅れとした$ \ \mathrm{q} \ $軸に実軸を割り当てている。ここでは，電機子巻線抵抗及び各種損失は無視する。
フェーザ図から$ \ \displaystyle -\dot E=E\mathrm{e}^{\mathrm {j}\pi }=-E \ $，$ \ \displaystyle \dot I={\dot I}_{\mathrm {q}}+{\dot I}_{\mathrm {d}}=\fbox {　（１）　} \ $，$ \ \displaystyle \dot V=V\mathrm{e}^{\mathrm {j}(\delta +\pi )} \ $となる。損失は無視したため，出力$ \ P_{\mathrm {OP}} \ $は入力に等しく，$ \ P_{\mathrm {OP}} \ $は①式となる。
\[
\begin{eqnarray}
P_{\mathrm {OP}}&=&\mathrm {Re}\left( 3\dot V\overline {\dot I}\right) =\fbox {　（２）　}　　・・・・・・・・・・・・・・・・・①
\end{eqnarray}
\] フェーザ図から，②及び③式が導かれる。
\[
\begin{eqnarray}
-V\cos\delta &=& \fbox {　（３）　}　　　　　　　&・・・・・・・・・・・・・・・・・② &\\[ 5pt ] -V\sin\delta &=& -X_{\mathrm {q}}I_{\mathrm {q}}　　　　　　　　　&・・・・・・・・・・・・・・・・・③ &
\end{eqnarray}
\] ②及び③式より，$ \ I_{\mathrm {d}} \ $及び$ \ I_{\mathrm {q}} \ $を求めて①式に代入すれば，出力トルク$ \ T \ $は④式になる。
\[
\begin{eqnarray}
T &=& \frac {pP_{\mathrm {OP}}}{\omega _{\mathrm {s}}} \\[ 5pt ] &=& \frac {p}{\omega _{\mathrm {s}}}\cdot \frac {3VE}{X_{\mathrm {d}}}\sin \delta +\frac {p}{\omega _{\mathrm {s}}}\cdot \frac {3V^{2}}{2}\left( \fbox {　（４）　}\right) \times \sin 2\delta　・・・・・・・④
\end{eqnarray}
\] ここで，$ \ p \ $は極対数である。一般に$ \ \delta \ $が$ \ \mathrm{65～70°} \ $付近で突極形同期電動機の出力トルクは最大となる。
突極機の場合，無負荷誘導起電力の大きさに依存しない④式右辺第二項が存在する。この成分のトルクを$ \ \fbox {　（５）　} \ $と呼ぶ。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　3V(I_{\mathrm {q}}\cos \delta +I_{\mathrm {d}}\sin \delta )　　　&（ロ）&　負荷トルク　　　&（ハ）&　リラクタンストルク \\[ 5pt ] &（ニ）&　\frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}　　　&（ホ）&　\frac {1}{X_{\mathrm {d}}}-\frac {1}{X_{\mathrm {q}}}　　　&（ヘ）&　E+X_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ] &（ト）&　-E-X_{\mathrm {d}}I_{\mathrm {d}}　　　&（チ）&　-I_{\mathrm {d}}-\mathrm {j}I_{\mathrm {q}}　　　&（リ）&　-E+X_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ] &（ヌ）&　\frac {1}{X_{\mathrm {d}}}+\frac {1}{X_{\mathrm {q}}}　　　&（ル）&　界磁トルク　　　&（ヲ）&　I_{\mathrm {q}}+\mathrm {j}I_{\mathrm {d}} \\[ 5pt ] &（ワ）&　3V(I_{\mathrm {d}}\cos \delta +I_{\mathrm {q}}\sin \delta )　　　&（カ）&　-I_{\mathrm {q}}-\mathrm {j}I_{\mathrm {d}}　　　&（ヨ）&　3V(-I_{\mathrm {q}}\cos \delta +I_{\mathrm {d}}\sin \delta )
\end{eqnarray}
\]

【ワンポイント解説】

本問は同期電動機のフェーザ図と書いてあるので，一見難しそうですが，中身はベクトルの数値計算なのでそれほど難易度の高い問題ではありません。符号に注意して解いて下さい。

1.オイラーの公式
極座標空間において，
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ] \end{eqnarray}
\] という関係があり，これをオイラーの公式といいます。

【解答】

(1)解答：カ
問題図より，$ \ {\dot I}_{\mathrm {q}}=-I_{\mathrm {q}} \ $，$ \ {\dot I}_{\mathrm {d}}=-\mathrm {j}I_{\mathrm {d}} \ $であるから，
\[
\begin{eqnarray}
\dot I &=& {\dot I}_{\mathrm {q}}+{\dot I}_{\mathrm {d}} \\[ 5pt ] &=& -I_{\mathrm {q}}-\mathrm {j}I_{\mathrm {d}}
\end{eqnarray}
\] と求められる。

(2)解答：イ
オイラーの公式より，$ \ \dot V \ $を展開すると，
\[
\begin{eqnarray}
\dot V &=& V\mathrm {e}^{\mathrm {j}(\delta +\pi )} \\[ 5pt ] &=& V\left[ \cos \left( \delta + \pi \right) +\mathrm {j}\sin \left( \delta + \pi \right) \right] \\[ 5pt ] &=& -V\left( \cos \delta +\mathrm {j}\sin \delta \right)
\end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
P_{\mathrm {OP}} &=& \mathrm {Re}\left( 3\dot V\overline {\dot I}\right) \\[ 5pt ] &=& \mathrm {Re}\left[ 3\cdot -V\left( \cos \delta +\mathrm {j}\sin \delta \right) \cdot \left(-I_{\mathrm {q}}+\mathrm {j}I_{\mathrm {d}}\right) \right] \\[ 5pt ] &=& 3V\left( I_{\mathrm {q}}\cos \delta +I_{\mathrm {d}}\sin \delta \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
問題図より，
\[
\begin{eqnarray}
-V\cos \delta &=&-E +X_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ] \end{eqnarray}
\] となる。

(4)解答：ニ
②，③より，
\[
\begin{eqnarray}
I_{\mathrm {d}} &=& \frac {E-V\cos \delta }{X_{\mathrm {d}}} \\[ 5pt ] I_{\mathrm {q}} &=& \frac {V\sin\delta}{X_{\mathrm {q}}}
\end{eqnarray}
\] となるので，これを①に代入すると，
\[
\begin{eqnarray}
P_{\mathrm {OP}} &=& 3V\left( I_{\mathrm {q}}\cos \delta +I_{\mathrm {d}}\sin \delta \right) \\[ 5pt ] &=& 3V\left( \frac {V\sin\delta}{X_{\mathrm {q}}}\cos \delta +\frac {E-V\cos \delta }{X_{\mathrm {d}}}\sin \delta \right) \\[ 5pt ] &=& \frac {3VE}{X_{\mathrm {d}}}\sin \delta +3V^{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) \sin \delta \cos \delta \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$\sin 2\delta =2\sin \delta \cos \delta $であるから，
\[
\begin{eqnarray}
P_{\mathrm {OP}}&=&\frac {3VE}{X_{\mathrm {d}}}\sin \delta +\frac {3V^{2}}{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) \times \sin 2\delta \\[ 5pt ] \end{eqnarray}
\] と求められる。よって出力トルクは，
\[
\begin{eqnarray}
T &=& \frac {pP_{\mathrm {OP}}}{\omega _{\mathrm {s}}} \\[ 5pt ] &=& \frac {p}{\omega _{\mathrm {s}}}\cdot \frac {3VE}{X_{\mathrm {d}}}\sin \delta +\frac {p}{\omega _{\mathrm {s}}}\cdot \frac {3V^{2}}{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) \times \sin 2\delta
\end{eqnarray}
\] となる。