【問題】
【難易度】★★☆☆☆(やや易しい)
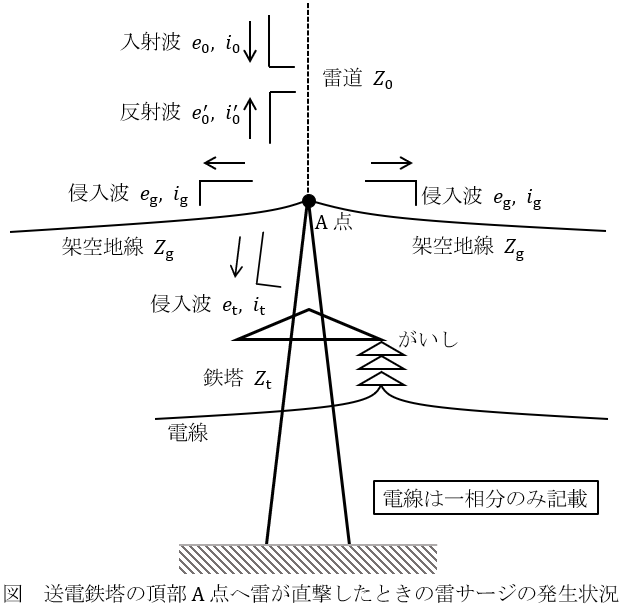
図に示すように,自己サージインピーダンス\( \ Z_{\mathrm {g}} \ \)の架空地線\( \ 1 \ \)条を有する三相\( \ 1 \ \)回線送電鉄塔の頂部\( \ \mathrm {A} \ \)点に雷の直撃を受けた。このときの頂部\( \ \mathrm {A} \ \)点の最大電圧について次の問に答えよ。ただし,雷サージの電圧,電流はそれぞれ\( \ e \ \),\( \ i \ \)で表すものとし,入射波の電圧波形は波高値\( \ e_{0} \ \)の方形波(矩形波),雷道のサージインピーダンスは\( \ Z_{0} \ \),塔脚接地抵抗を含む鉄塔のサージインピーダンスは\( \ Z_{\mathrm {t}} \ \)とする。なお,鉄塔と架空地線の間の相互サージインピーダンスは無視するものとする。
(1) 鉄塔への雷の直撃により,鉄塔電位が上昇し電線へ放電する現象の名称を答えよ。
(2) 架空送電設備における,架空地線以外の雷害対策(雷サージの発生防止対策又は雷サージ発生時の設備損傷防止対策)を二つ答えよ。
(3) 雷道を通る入射波を\( \ e_{0} \ \),\( \ i_{0} \ \),雷道への反射波を\( \ e_{0}^{\prime } \ \),\( \ i_{0}^{\prime } \ \),架空地線への侵入波を\( \ e_{\mathrm {g}} \ \),\( \ i_{\mathrm {g}} \ \),鉄塔への侵入波を\( \ e_{\mathrm {t}} \ \),\( \ i_{\mathrm {t}} \ \)としたとき,雷撃直後の頂部\( \ \mathrm {A} \ \)点における電圧の関係と電流の関係について成り立つ式をそれぞれ示せ。
(4) 頂部\( \ \mathrm {A} \ \)点の最大電圧となる\( \ e_{\mathrm {t}} \ \)を,\( \ e_{0} \ \),\( \ Z_{0} \ \),\( \ Z_{\mathrm {g}} \ \)及び\( \ Z_{\mathrm {t}} \ \)を用いて表せ。
(5) \( \ e_{0}=3 \ 000 \ \mathrm {kV} \ \),\( \ Z_{0}=400 \ \mathrm {\Omega } \ \),\( \ Z_{\mathrm {g}}=500 \ \mathrm {\Omega } \ \),\( \ Z_{\mathrm {t}}=100 \ \mathrm {\Omega } \ \)のとき,頂部\( \ \mathrm {A} \ \)点の最大電圧となる\( \ e_{\mathrm {t}} \ \)の値を求めよ。
【ワンポイント解説】
鉄塔落雷時の雷サージの伝搬に関する問題です。
論述問題と計算問題を組み合わせた問題ですが,いずれも一度は学習されていると思いますので,本番でもぜひ選択したい問題です。
平成21年電力管理問3にほぼ同じ計算問題が出題されていましたので,多くの受験生が選択し正答できた問題かと思います。
1.分布定数回路における接続点での関係式
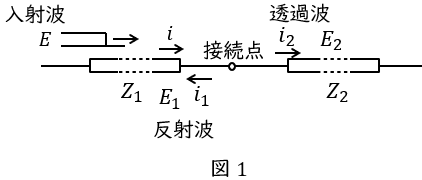
図1のような,特性インピーダンスが\( \ Z_{1} \ \)及び\( \ Z_{2} \ \)の非常に長い無損失線路が接続されているときの接続点での関係式を考えます。
図の左側から波高値\( \ E \ \)の電圧波が進入すると,接続点で一部の電圧が反射し,残りの電圧が透過します。このとき,入射波による電流を\( \ i \ \),反射波により生じる電圧及び電流を\( \ E_{1} \ \)及び\( \ i_{1} \ \),透過波により生じる電圧及び電流を\( \ E_{2} \ \)及び\( \ i_{2} \ \)とすると,以下の電圧と電流の関係式が成り立ちます。
\[
\begin{eqnarray}
E +E_{1}&=&E_{2} \\[ 5pt ]
i -i_{1}&=&i_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,各電圧と電流には,
\[
\begin{eqnarray}
E&=&Z_{1}i \\[ 5pt ]
E_{1}&=&Z_{1}i_{1} \\[ 5pt ]
E_{2}&=&Z_{2}i_{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立します。
※ 本問に合わせ\( \ i_{1} \ \)は左向きを正としています。右向きを正とする場合もあるので,向きに注意しましょう。
2.架空地線
<架空地線の役割>
架空地線は電線の上部、主に鉄塔の一番上に設ける裸電線で,以下のような役割があります。
①送電線への直撃雷を防止する。
②誘導雷(雷雲の電荷により反対の電荷が電線に現れ,落雷により雷雲の電荷がなくなるために電線で大きな電荷の移動が起こる現象)を軽減する。
③通信線への電磁誘導障害を軽減する。
<架空地線落雷時の対策>
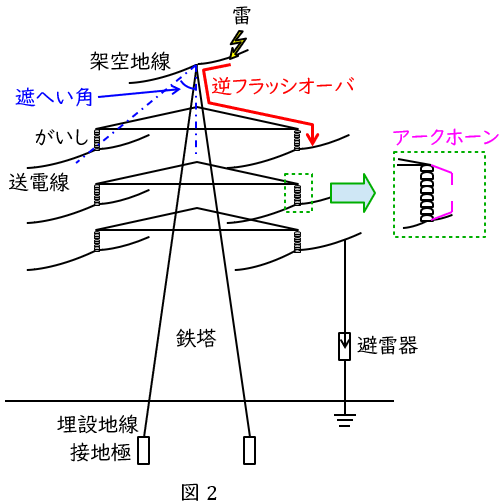
また,架空地線や鉄塔に落雷した際の逆フラッシオーバに対する対策として,以下のような対策が取られます。
①埋設地線で鉄塔と大地の接地抵抗を小さくする。
②アークホーンでがいしの損傷を防止する。(逆フラッシオーバ自体の対策ではありません。)
③\( \ 2 \ \)回線送電線におけるがいしの連結個数に差をつけて(不平衡絶縁方式),両回線同時事故を防ぐ。
3.送電線用避雷装置
過電圧が発生した際に導通し,その後の続流を制限する装置です。アークホーンには一旦フラッシオーバが発生すると続流を遮断する機能がないため,変電所の遮断器等が動作し送電線事故に至る可能性がありますが,送電線用避雷装置には瞬時に続流を遮断する機能があるため,送電線の雷事故発生を防ぐことができます。
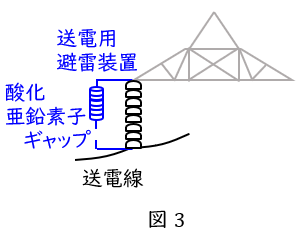
図3に示すような酸化亜鉛素子をがいしと並列して設置するもので,酸化亜鉛素子に直列ギャップを設けるのが一般的です。
【解答】
(1)鉄塔への雷の直撃により,鉄塔電位が上昇し電線へ放電する現象の名称
(ポイント)
・ワンポイント解説「2.架空地線」の通りです。
(試験センター解答例)
逆フラッシオーバ又は鉄塔逆フラッシオーバ
(2)架空送電設備における,架空地線以外の雷害対策(雷サージの発生防止対策又は雷サージ発生時の設備損傷防止対策)を二つ
(ポイント)
・ワンポイント解説「2.架空地線」の通りです。
・不平衡絶縁は停電事故防止対策であり,雷サージの発生防止対策又は雷サージ発生時の設備損傷防止対策ではないので,ここでは正答にはならないと考えられます。
(試験センター解答例)
・アークホーンの設置
・送電用避雷装置の設置
・塔脚接地抵抗の低減(埋設地線や連接接地を設ける)
(3)雷撃直後の頂部\( \ \mathrm {A} \ \)点における電圧の関係と電流の関係について成り立つ式
\( \ \mathrm {A} \ \)点における電圧の関係式及び電流の関係式は,ワンポイント解説「1.分布定数回路における接続点での関係式」の通り,
\[
\begin{eqnarray}
e_{0}+e^{\prime }_{0}&=&e_{\mathrm {g}}=e_{\mathrm {t}} & \ ・・・・・・・・・・・・・ ①& \\[ 5pt ]
i_{0}-i_{0}^{\prime }&=&2i_{\mathrm {g}}+i_{\mathrm {t}} & \ ・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)頂部\( \ \mathrm {A} \ \)点の最大電圧となる\( \ e_{\mathrm {t}} \ \)
頂部\( \ \mathrm {A} \ \)点が最大電圧となるのは,雷撃直後であり,そのときの鉄塔頂部\( \ \mathrm {A} \ \)点の電圧は\( \ e_{\mathrm {t}} \ \)である。
各部の電圧と電流の関係式は,ワンポイント解説「1.分布定数回路における接続点での関係式」の通り,
\[
\begin{eqnarray}
e_{0}&=&Z_{0}i_{0} &・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
e^{\prime }_{0}&=&Z_{0}i_{0}^{\prime } &・・・・・・・・・・・・・・・・・ ④& \\[ 5pt ]
e_{\mathrm {g}}&=&Z_{\mathrm {g}}i_{\mathrm {g}} &・・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
e_{\mathrm {t}}&=&Z_{\mathrm {t}}i_{\mathrm {t}} &・・・・・・・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
となるので,③~⑥を電流値について整理し,②に代入すると,
\[
\begin{eqnarray}
i_{0}-i_{0}^{\prime }&=&2i_{\mathrm {g}}+i_{\mathrm {t}} \\[ 5pt ]
\frac {e_{0}}{Z_{0}}-\frac {e^{\prime }_{0}}{Z_{0}}&=&\frac {2e_{\mathrm {g}}}{Z_{\mathrm {g}}}+\frac {e_{\mathrm {t}}}{Z_{\mathrm {t}}} \\[ 5pt ]
e_{0}-e^{\prime }_{0}&=&Z_{0}\left( \frac {2e_{\mathrm {g}}}{Z_{\mathrm {g}}}+\frac {e_{\mathrm {t}}}{Z_{\mathrm {t}}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,①より\( \ e_{\mathrm {g}}=e_{\mathrm {t}} \ \)であるから,
\[
\begin{eqnarray}
e_{0}-e^{\prime }_{0}&=&Z_{0}\left( \frac {2e_{\mathrm {t}}}{Z_{\mathrm {g}}}+\frac {e_{\mathrm {t}}}{Z_{\mathrm {t}}}\right) \\[ 5pt ]
&=&Z_{0}e_{\mathrm {t}}\left( \frac {2}{Z_{\mathrm {g}}}+\frac {1}{Z_{\mathrm {t}}}\right) \\[ 5pt ]
&=&\frac {Z_{0}\left( 2Z_{\mathrm {t}}+Z_{\mathrm {g}}\right) }{Z_{\mathrm {g}}Z_{T}}e_{\mathrm {t}} \ &・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ①+⑦ \ \)より,
\[
\begin{eqnarray}
2e_{0}&=&e_{\mathrm {t}}+\frac {Z_{0}\left( 2Z_{\mathrm {t}}+Z_{\mathrm {g}}\right) }{Z_{\mathrm {g}}Z_{\mathrm {t}}}e_{\mathrm {t}} \\[ 5pt ]
&=&e_{\mathrm {t}}\left\{ 1+\frac {Z_{0}\left( 2Z_{\mathrm {t}}+Z_{\mathrm {g}}\right) }{Z_{\mathrm {g}}Z_{\mathrm {t}}}\right\} \\[ 5pt ]
&=&e_{\mathrm {t}}\frac {Z_{\mathrm {g}}Z_{\mathrm {t}}+2Z_{\mathrm {t}}Z_{0}+Z_{0}Z_{\mathrm {g}}}{Z_{\mathrm {g}}Z_{\mathrm {t}}} \\[ 5pt ]
e_{\mathrm {t}}&=&e_{0}\frac {2Z_{\mathrm {g}}Z_{\mathrm {t}}}{Z_{\mathrm {g}}Z_{\mathrm {t}}+2Z_{\mathrm {t}}Z_{0}+Z_{0}Z_{\mathrm {g}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)頂部\( \ \mathrm {A} \ \)点の最大電圧となる\( \ e_{\mathrm {t}} \ \)の値
(4)解答式に,\( \ e_{0}=3 \ 000 \ \mathrm {[kV]} \ \),\( \ Z_{0}=400 \ \mathrm {[\Omega ]} \ \),\( \ Z_{\mathrm {g}}=500 \ \mathrm {[\Omega ]} \ \),\( \ Z_{\mathrm {t}}=100 \ \mathrm {[\Omega ]} \ \)を代入すると,
\[
\begin{eqnarray}
e_{\mathrm {t}}&=&e_{0}\frac {2Z_{\mathrm {g}}Z_{\mathrm {t}}}{Z_{\mathrm {g}}Z_{\mathrm {t}}+2Z_{\mathrm {t}}Z_{0}+Z_{0}Z_{\mathrm {g}}} \\[ 5pt ]
&=&3 \ 000\times 10^{3}\times \frac {2\times 500\times 100}{500\times 100+2\times 100\times 400+400\times 500} \\[ 5pt ]
&≒&909 \ 090 \ \mathrm {[V]} → 909 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん