【問題】
【難易度】★★☆☆☆(やや易しい)
三相誘導電動機の\( \ \mathrm {L} \ \)形等価回路において,\( \ r_{1} \ [\mathrm {\Omega}] \ \)は一次抵抗,\( \ x_{1} \ [\mathrm {\Omega}] \ \)は一次リアクタンス,\( \ r_{2}^{\prime } \ [\mathrm {\Omega}] \ \)は一次側に換算した二次抵抗,\( \ x_{2}^{\prime } \ [\mathrm {\Omega}] \ \)は一次側に換算した二次リアクタンス,\( \ V_{1} \ [\mathrm {V}] \ \)は一次相電圧,\( \ I_{1} \ [\mathrm {A}] \ \)は一次電流,\( \ I_{2}^{\prime} \ [\mathrm {A}] \ \)は一次側に換算した二次電流,\( \ s \ \)は滑り,\( \ \omega _{\mathrm {s}} \ [\mathrm {rad/s}] \ \)は同期角速度であるとする。次の問に答えよ。
(1) \( \ \mathrm {L} \ \)形等価回路の励磁回路及び機械損を無視した場合について,次のa及びbに答えよ。
a.最大トルク\( \ T_{\mathrm {max}} \ \)を生じるときの滑り\( \ s_{\mathrm {m}} \ \)を導出せよ。
b.そのときの最大トルク\( \ T_{\mathrm {max}} \ \)を導出せよ。
(2) 上記小問(1)の条件に加え,一次抵抗\( \ r_{1} \ \)を無視した場合について,次のc及びdに答えよ。
c.滑り\( \ s \ \)のときのトルク\( \ T \ \)に対する最大トルク\( \ T_{\mathrm {max}} \ \)の比\( \ \displaystyle \frac {T_{\mathrm {max}}}{T} \ \)を,最大トルク\( \ T_{\mathrm {max}} \ \)のときの滑り\( \ s_{\mathrm {m}} \ \)及びトルク\( \ T \ \)のときの滑り\( \ s \ \)によって表せ。
d.この電動機の等価回路定数は次のような値であった。
\[
\begin{eqnarray}
x_{1} &=& 0.356 \ \Omega \\[ 5pt ]
r_{2}^{\prime} &=& 0.144 \ \Omega \\[ 5pt ]
x_{2}^{\prime} &=& 0.356 \ \Omega \\[ 5pt ]
\end{eqnarray}
\]
この電動機で,あるトルク\( \ T \ \)において\( \ \displaystyle \frac {T_{\mathrm {max}}}{T}=2 \ \)であった。このときの滑り\( \ s \ [%] \ \)を求めよ。
【ワンポイント解説】
誘導電動機を理解するには非常に良い問題で,過去にも類題が出題されています。難易度はそれほど高くありませんが,計算式が長いため,\( \ 30 \ \)分以内で解くことはかなり難しいと思います。
1.三相誘導電動機の\( \ \mathrm {L} \ \)形等価回路
三相誘導電動機の一相あたりの\( \ \mathrm {L} \ \)形等価回路は図1のようになります。\( \ \mathrm {L} \ \)形等価回路は確実に描けるようにしておきましょう。
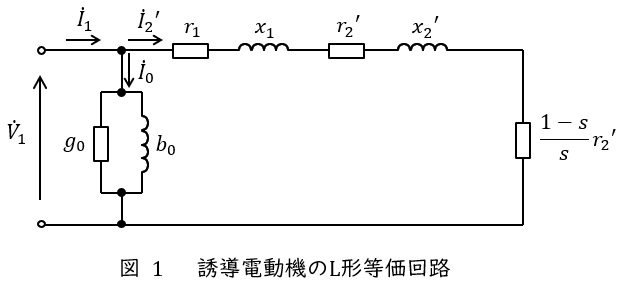
\[
\begin{eqnarray}
{\dot V}_{1}&:&一次電圧 \\[ 5pt ]
{\dot I}_{1}&:&一次電流 \\[ 5pt ]
{\dot I}_{0}&:&励磁電流 \\[ 5pt ]
{\dot I}^{\prime}_{2}&:&一次側に換算した二次電流 \\[ 5pt ]
r_{1}&:&一次抵抗 \\[ 5pt ]
x_{1}&:&一次リアクタンス \\[ 5pt ]
r_{2}^{\prime}&:&一次側に換算した二次抵抗 \\[ 5pt ]
x_{2}^{\prime}&:&一次側に換算した二次リアクタンス \\[ 5pt ]
g_{0}&:&励磁コンダクタンス \\[ 5pt ]
b_{0}&:&励磁サセプタンス \\[ 5pt ]
s&:&滑り
\end{eqnarray}
\]
【解答】
(1)a.最大トルク\( \ T_{\mathrm {max}} \ \)を生じるときの滑り\( \ s_{\mathrm {m}} \ \)
図1のように\( \ \mathrm {L} \ \)形等価回路は描け,励磁コンダクタンスと励磁サセプタンスは無視できるので,一次側に換算した二次電流\( \ I^{\prime}_{2} \ \)は,
\[
\begin{eqnarray}
I^{\prime}_{2}&=&\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ]
&=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\]
と求められる。電動機の出力を\( \ P_{\mathrm {o}} \ \),その時の角速度を\( \ \omega \ \)とすると,トルク\( \ T \ \)は,
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {(1-s)P_{2}}{(1-s)\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
T&=&\frac {3r_{2}^{\prime}}{\omega _{\mathrm {s}}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。ここでトルクが最大となるためには,上式の分母が最小となる滑り\( \ s \ \)を求めればよい。よって,
\[
\begin{eqnarray}
A&=&s\cdot \left[\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}\right] \\[ 5pt ]
&=&\left( r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}\right) s + 2r_{1} r_{2}^{\prime} +\frac {{r_{2}^{\prime}}^{2}}{s} \\[ 5pt ]
\end{eqnarray}
\]
と置き,両辺を\( \ s \ \)について微分すると,
\[
\begin{eqnarray}
\frac {dA}{ds}&=&r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2} -\frac {{r_{2}^{\prime}}^{2}}{s^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle \frac {dA}{ds}=0 \ \)となる滑り\( \ s_{\mathrm {m}} \ \)は,
\[
\begin{eqnarray}
r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2} -\frac {{r_{2}^{\prime}}^{2}}{s_{\mathrm {m}}^{2}}=0 \\[ 5pt ]
s_{\mathrm {m}}=\frac {r_{2}^{\prime}}{\sqrt{ r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}}
\end{eqnarray}
\]
と求められる。
(1)b.最大トルク\( \ T_{\mathrm {max}} \ \)
(1)aより,\( \ s_{\mathrm {m}} \ \)をトルク\( \ T \ \)の式に代入すると,
\[
\begin{eqnarray}
T_{\mathrm {max}}&=&\frac {3r_{2}^{\prime}}{\omega _{\mathrm {s}}s_{m}}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s_{m}}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ]
&=&\frac {3\sqrt{ r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}}{\omega _{\mathrm {s}}}\cdot \frac {V_{1}^{2}}{\left( r_{1}+\sqrt{ r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ]
&=&\frac {3\sqrt{ r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}}{2\omega _{\mathrm {s}}}\cdot \frac {V_{1}^{2}}{r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}+r_{1}\sqrt{r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}} \\[ 5pt ]
&=&\frac {3}{2\omega _{\mathrm {s}}}\cdot \frac {V_{1}^{2}}{r_{1}+\sqrt{r_{1}^{2}+\left( x_{1}+x_{2}^{\prime}\right) ^{2}}}
\end{eqnarray}
\]
と求められる。
(2)c.トルク\( \ T \ \)に対する最大トルク\( \ T_{\mathrm {max}} \ \)の比\( \ \displaystyle \frac {T_{\mathrm {max}}}{T} \ \)
(1)より,\( \ r_{1} \ \)を無視すると,\( \ \displaystyle \frac {T_{\mathrm {max}}}{T} \ \)は,
\[
\begin{eqnarray}
\frac {T_{\mathrm {max}}}{T}&=&\frac {\displaystyle \frac {3}{2\omega _{\mathrm {s}}}\cdot \frac {V_{1}^{2}}{\displaystyle \sqrt{\left( x_{1}+x_{2}^{\prime}\right) ^{2}}}}{\displaystyle \frac {3r_{2}^{\prime}}{\omega _{\mathrm {s}}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( \frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{2}\cdot \frac {1}{x_{1}+x_{2}^{\prime}}}{\displaystyle \frac {r_{2}^{\prime}}{s}\cdot \frac {1}{\displaystyle \left( \frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ]
&=&\frac {\displaystyle s\left[ \left( \frac{r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] }{2r_{2}^{\prime }\left( x_{1}+x_{2}^{\prime }\right) }
\end{eqnarray}
\]
となる。ここで,\( \ s_{\mathrm {m}} \ \)は\( \ r_{1} \ \)を無視すると,
\[
\begin{eqnarray}
s_{\mathrm {m}}=\frac {r_{2}^{\prime}}{x_{1}+x_{2}^{\prime}} \\[ 5pt ]
x_{1}+x_{2}^{\prime}=\frac {r_{2}^{\prime}}{s_{\mathrm {m}}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,\( \ \displaystyle \frac {T_{\mathrm {max}}}{T} \ \)は,
\[
\begin{eqnarray}
\frac {T_{\mathrm {max}}}{T}&=&\frac {\displaystyle s\left[ \left( \frac{r_{2}^{\prime }}{s}\right) ^{2}+\left( \frac {r_{2}^{\prime}}{s_{\mathrm {m}}}\right) ^{2}\right] }{\displaystyle 2r_{2}^{\prime }\left( \frac {r_{2}^{\prime}}{s_{\mathrm {m}}}\right) } \\[ 5pt ]
&=&\frac {\displaystyle s\left[ \left( \frac{1}{s}\right) ^{2}+\left( \frac {1}{s_{\mathrm {m}}}\right) ^{2}\right] }{\displaystyle 2\left( \frac {1}{s_{\mathrm {m}}}\right) } \\[ 5pt ]
&=&\frac {ss_{\mathrm {m}}}{2} \left( \frac{1}{s^{2}}+\frac {1}{s_{\mathrm {m}}^{2}}\right) \\[ 5pt ]
&=&\frac {1}{2} \left( \frac{s_{\mathrm {m}}}{s}+\frac {s}{s_{\mathrm {m}}}\right)
\end{eqnarray}
\]
と求められる。
(2)d.諸条件の時の滑り\( \ s \ [%] \ \)
題意より,\( \ \displaystyle \frac {T_{\mathrm {max}}}{T}=2 \ \)であるから,
\[
\begin{eqnarray}
\frac {T_{\mathrm {max}}}{T}&=& \frac {1}{2} \left( \frac{s_{\mathrm {m}}}{s}+\frac {s}{s_{\mathrm {m}}}\right) &=&2 \\[ 5pt ]
\frac{s_{\mathrm {m}}}{s}+\frac {s}{s_{\mathrm {m}}}&=& 4 \\[ 5pt ]
s^{2}-4s_{\mathrm {m}}s+s_{\mathrm {m}}^{2}&=& 0 \\[ 5pt ]
s&=& ( 2±\sqrt {3} )s_{\mathrm {m}}
\end{eqnarray}
\]
となる。ここで,\( \ x_{1} = 0.356 \ \Omega ,r_{2}^{\prime} = 0.144 \ \Omega ,x_{2}^{\prime} = 0.356 \ \Omega \)であるから,\( \ s_{\mathrm {m}} \ \)は,
\[
\begin{eqnarray}
s_{\mathrm {m}}&=&\frac {r_{2}^{\prime}}{x_{1}+x_{2}^{\prime}} \\[ 5pt ]
&=&\frac {0.144}{0.356+0.356} \\[ 5pt ]
&≒&0.20225 \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
s&=& ( 2±\sqrt {3} )s_{\mathrm {m}} \\[ 5pt ]
s&≒&0.75481,0.05419 \\[ 5pt ]
\end{eqnarray}
\]
\( \ s < s_{\mathrm {m}} \ \)なので,\( \ s=5.42 \ [%] \ \)となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん