《機械》〈回転機〉[R02:問5]三相誘導電動機のメカニズムに関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，三相誘導電動機に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

三相誘導電動機の固定子巻線に周波数$ \ f_{\mathrm {1}} \ $の平衡三相電流を流すと，回転磁界を生じる。この回転磁界により固定子巻線に誘導起電力を発生する。その$ \ 1 \ $相当たりの誘導起電力の実効値$ \ E_{\mathrm {1}} \ $を，$ \ 1 \ $相当たりの直列有効巻数を$ \ k_{\mathrm {w1}}N_{\mathrm {1}} \ $とし，ギャップ磁束$ \ \mathit {\Phi } \ $で表すと，
\[
\begin{eqnarray}
E_{\mathrm {1}} &=& \ \fbox {　（１）　} \ \\[ 5pt ] \end{eqnarray}
\] となる。無負荷の場合，この誘導起電力は固定子巻線の三相電流に対し，位相が$ \ \fbox {　（２）　} \ $。

回転磁界は仮想的な磁極が同期角速度$ \ \omega _{\mathrm {1}}\left( =2\pi f_{\mathrm {1}}\right) \ $で回転しているものと考えることができる。今，回転磁界は空間的に正弦波分布をしているとし，回転子が回転磁界と同じ方向に角速度$ \ \omega _{\mathrm {2}} \ $で回転しているとすれば，回転角速度の関係が$ \ \fbox {　（３）　} \ $では，回転磁界との相対速度により，回転子導体には起電力が誘導される。回転子が静止しているときは回転子巻線の$ \ 1 \ $相当たりの直列有効巻数を$ \ k_{\mathrm {w2}}N_{\mathrm {2}} \ $とすれば，$ \ 1 \ $相当たりの誘導起電力の実効値$ \ E_{\mathrm {2}} \ $は次のように表すことができる。
\[
\begin{eqnarray}
E_{\mathrm {2}} &=& \ \fbox {　（４）　} \ \\[ 5pt ] \end{eqnarray}
\] 回転子が滑り$ \ s \ $で回転しているとき，二次導体と回転磁界との相対速度は$ \ s\omega _{\mathrm {1}} \ $となり，誘導起電力の大きさと周波数はこれに比例するので，二次誘導起電力の実効値は$ \ sE_{\mathrm {2}} \ $，その周波数$ \ f_{\mathrm {2}} \ $は$ \ \fbox {　（５）　} \ $となる。

かご形回転子の二次導体は端絡環で短絡されているため，各導体には二次誘導起電力により二次電流が流れる。二次回路には抵抗のほか，漏れリアクタンスがある。今，二次巻線$ \ 1 \ $相の抵抗を$ \ r_{\mathrm {2}} \ $，回転子が静止しているときの漏れリアクタンスを$ \ x_{\mathrm {2}} \ $とすると，滑り$ \ s \ $のときの二次$ \ 1 \ $相のインピーダンス$ \ {\dot Z}_{\mathrm {2}} \ $は，次のようになる。
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {2}} &=& \ \fbox {　（６）　} \ \\[ 5pt ] \end{eqnarray}
\]

したがって，電動機が滑り$ \ s \ $で運転しているときの二次電流の大きさ$ \ I_{\mathrm {2}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {2}} &=& \ \fbox {　（７）　} \ \\[ 5pt ] \end{eqnarray}
\] となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {r_{\mathrm {2}}}{s}+\mathrm {j}sx_{\mathrm {2}}　　　　　&（ロ）&　4.44sf_{\mathrm {2}}k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi }　　　　　&（ハ）&　約90°進んでいる \\[ 5pt ] &（ニ）&　\omega _{\mathrm {2}}≠\omega _{\mathrm {1}}　　　　　&（ホ）&　sf_{\mathrm {2}}　　　　　&（ヘ）&　4.44sf_{\mathrm {1}}k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi } \\[ 5pt ] &（ト）&　4.44f_{\mathrm {1}}k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi }　　　　　&（チ）&　約90°遅れている　　　　　&（リ）&　\frac {E_{\mathrm {2}}}{\displaystyle \sqrt {\frac {r_{\mathrm {2}}^{2}}{s}+x_{\mathrm {2}}^{2}}} \\[ 5pt ] &（ヌ）&　\omega _{\mathrm {2}}=\omega _{\mathrm {1}}　　　　　&（ル）&　r_{\mathrm {2}}+sx_{\mathrm {2}}　　　　　&（ヲ）&　r_{\mathrm {2}}+\mathrm {j}sx_{\mathrm {2}} \\[ 5pt ] &（ワ）&　\frac {sE_{\mathrm {2}}}{ \sqrt {r_{\mathrm {2}}^{2}+\left( sx_{\mathrm {2}}\right) ^{2}}}　　　　　&（カ）&　同一である　　　　　&（ヨ）&　s\omega _{\mathrm {1}} \\[ 5pt ] &（タ）&　\frac {E_{\mathrm {1}}}{\displaystyle \sqrt {\frac {r_{\mathrm {2}}^{2}}{s}+x_{\mathrm {2}}^{2}}}　　　　　&（レ）&　sf_{\mathrm {1}}　　　　　&（ソ）&　\sqrt {3}f_{\mathrm {1}}k_{\mathrm {w1}}N_{\mathrm {1}}\mathit {\Phi } \\[ 5pt ] &（ツ）&　4.44sf_{\mathrm {1}}k_{\mathrm {w1}}N_{\mathrm {1}}\mathit {\Phi }　　　　　&（ネ）&　4.44f_{\mathrm {1}}k_{\mathrm {w1}}N_{\mathrm {1}}\mathit {\Phi }　　　　　&&　 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘導電動機の誘導起電力等の導出に関する問題です。
誘導電動機の問題は公式を丸暗記していてもある程度得点できる問題が多いですが，本問は$ \ 1 \ $種らしく公式の中身を問うような問題となっています。
本問のようにある程度導出過程を理解していると誘導電動機に関する理解が深まると思います。

1.ファラデーの法則による磁束$ \ \phi \ $と起電力$ \ e \ $の関係
巻き数$ \ N \ $のコイルに磁束$ \ \phi \ $が貫いたときの起電力$ \ e \ $はファラデーの法則より，
\[
\begin{eqnarray}
e &=&-N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] の関係があり，このとき流した電流を$ \ I \ $，コイルの自己インダクタンス$ \ L \ $とすると，
\[
\begin{eqnarray}
LI &=&N\phi \\[ 5pt ] \end{eqnarray}
\] の関係があります。したがって，$ \ \phi \ $と$ \ I \ $は比例関係にあるので，誘導電動機における磁束を$ \ \phi =\mathit {\Phi }_{\mathrm {m}}\sin \omega t \ $と置くことができ，
\[
\begin{eqnarray}
e &=&-N\frac {\mathrm {d}}{\mathrm {d}t}\left( \mathit {\Phi }_{\mathrm {m}}\sin \omega t\right) \\[ 5pt ] &=&-\omega N\mathit {\Phi }_{\mathrm {m}}\cos \omega t \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ネ
ワンポイント解説「1.ファラデーの法則による磁束$ \ \phi \ $と起電力$ \ e \ $の関係」の通り，ギャップ磁束を$ \ \phi =\mathit {\Phi }\sin \omega t \ $とすると，誘導起電力$ \ e_{\mathrm {1}} \ $は，
\[
\begin{eqnarray}
e_{\mathrm {1}} &=&-k_{\mathrm {w1}}N_{\mathrm {1}}\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] &=&-k_{\mathrm {w1}}N_{\mathrm {1}}\frac {\mathrm {d}}{\mathrm {d}t}\left( \mathit {\Phi }\sin \omega t\right) \\[ 5pt ] &=&-\omega k_{\mathrm {w1}}N_{\mathrm {1}}\mathit {\Phi }\cos \omega t \\[ 5pt ] &=&-2\pi f_{\mathrm {1}} k_{\mathrm {w1}}N_{\mathrm {1}}\mathit {\Phi }\cos \omega t \\[ 5pt ] \end{eqnarray}
\] となり，その実効値$ \ E_{\mathrm {1}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {1}} &=&\frac {2\pi }{\sqrt {2}} f_{\mathrm {1}} k_{\mathrm {w1}}N_{\mathrm {1}}\mathit {\Phi } \\[ 5pt ] &≒&4.44f_{\mathrm {1}} k_{\mathrm {w1}}N_{\mathrm {1}}\mathit {\Phi } \\[ 5pt ] \end{eqnarray}
\] と求められます。

(2)解答：チ
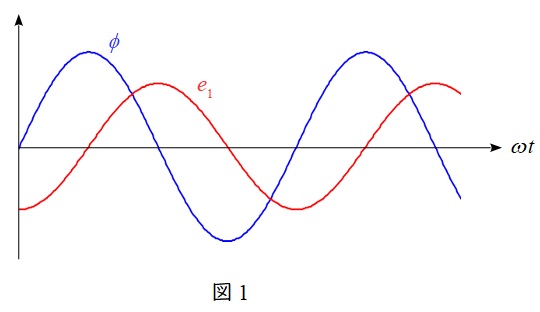
(1)で求めたギャップ磁束$ \ \phi \ $と誘導起電力$ \ e_{\mathrm {1}} \ $を図に示すと図1のようになり，誘導起電力$ \ e_{\mathrm {1}} \ $はギャップ磁束$ \ \phi \ $（∝固定子巻線の三相電流$ \ I \ $）より約$ \ 90° \ $遅れていることがわかる。

(3)解答：ニ
回転磁界が$ \ \omega _{\mathrm {1}} \ $で回転し，回転子が回転磁界と同じ方向に角速度$ \ \omega _{\mathrm {2}} \ $で回転しているとき，$ \ \omega _{\mathrm {1}}-\omega _{\mathrm {2}} \ $の角速度により起電力が誘導される。したがって，空欄穴埋として正しいのは$ \ \omega _{\mathrm {1}}≠\omega _{\mathrm {2}} \ $となる。

(4)解答：ト
二次側の誘導起電力$ \ e_{\mathrm {2}} \ $は，一次側の誘導起電力と同様に考えると，
\[
\begin{eqnarray}
e_{\mathrm {2}} &=&-k_{\mathrm {w2}}N_{\mathrm {2}}\frac {\mathrm {d}\phi _{\mathrm {2}} }{\mathrm {d}t} \\[ 5pt ] &=&-k_{\mathrm {w2}}N_{\mathrm {2}}\frac {\mathrm {d}}{\mathrm {d}t}\left\{ \mathit {\Phi }\sin \left( \omega _{\mathrm {1}}-\omega _{\mathrm {2}}\right) t\right\} \\[ 5pt ] &=&-\left( \omega _{\mathrm {1}}-\omega _{\mathrm {2}}\right) k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi }\cos \left( \omega _{\mathrm {1}}-\omega _{\mathrm {2}}\right) t \\[ 5pt ] &=&-2\pi \left( f _{\mathrm {1}}-f _{\mathrm {2}}\right) k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi }\cos \left( \omega _{\mathrm {1}}-\omega _{\mathrm {2}}\right) t \\[ 5pt ] \end{eqnarray}
\] となる。回転子が静止しているとき，$ \ \omega _{\mathrm {2}} =2\pi f_{\mathrm {2}}=0 \ $であるので，
\[
\begin{eqnarray}
e_{\mathrm {2}} &=&-2\pi f _{\mathrm {1}} k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi }\cos \omega _{\mathrm {1}} t \\[ 5pt ] \end{eqnarray}
\] となり，その実効値$ \ E_{\mathrm {2}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {2}} &=&\frac {2\pi }{\sqrt {2}} f_{\mathrm {1}} k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi }\\[ 5pt ] &≒&4.44f_{\mathrm {1}} k_{\mathrm {w2}}N_{\mathrm {2}}\mathit {\Phi }\\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：レ
$ \ \omega _{\mathrm {2}}=s\omega _{\mathrm {1}} \ $より，
\[
\begin{eqnarray}
2\pi f_{\mathrm {2}} &=&s\cdot 2\pi f_{\mathrm {1}} \\[ 5pt ] f_{\mathrm {2}} &=&sf_{\mathrm {1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)解答：ヲ
巻線抵抗$ \ r_{\mathrm {2}} \ $は角周波数により変化しないが，漏れリアクタンス$ \ x_{\mathrm {2}} \ $は角周波数$ \ \omega _{\mathrm {2}} \ $に比例する。静止時の角周波数は$ \ \omega _{\mathrm {1}} \ $，滑り$ \ s \ $で運転時の角周波数は$ \ s\omega _{\mathrm {1}} \ $であるから，滑り$ \ s \ $で運転時の漏れリアクタンスは$ \ sx_{\mathrm {2}} \ $となる。したがって，滑り$ \ s \ $のときの二次$ \ 1 \ $相のインピーダンス$ \ {\dot Z}_{\mathrm {2}} \ $は，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {2}} &=& r_{\mathrm {2}}+\mathrm {j}sx_{\mathrm {2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(7)解答：ワ
インピーダンス$ \ {\dot Z}_{\mathrm {2}} \ $の大きさ$ \ Z_{\mathrm {2}} \ $は，
\[
\begin{eqnarray}
Z_{\mathrm {2}} &=& \sqrt {{r_{\mathrm {2}}}^{2}+\left( sx_{\mathrm {2}}\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，題意より二次誘導起電力の実効値は$ \ sE_{\mathrm {2}} \ $であるから，二次電流の大きさ$ \ I_{\mathrm {2}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {2}} &=&\frac {sE_{\mathrm {2}}}{Z_{\mathrm {2}}} \\[ 5pt ] &=&\frac {sE_{\mathrm {2}}}{ \sqrt {r_{\mathrm {2}}^{2}+\left( sx_{\mathrm {2}}\right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。