《機械》〈パワーエレクトロニクス〉[H23:問5] 交流フィルタ設備に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，交流フィルタ設備に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

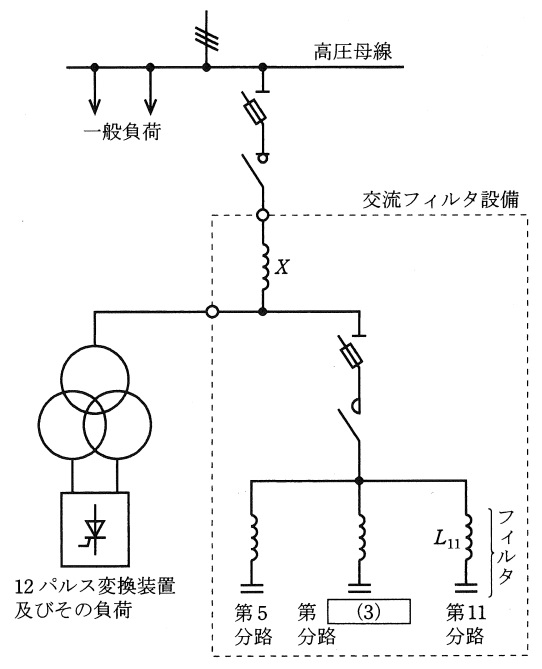
図の破線内は，三相$ \ 6 \ 600 \ \mathrm {[V]} \ $，$ \ 60 \ \mathrm {[Hz]} \ $の高圧母線から給電されるサイリスタ変換装置用の交流フィルタ設備の例である。変換装置は$ \ 12 \ $パルスで，変換装置用変圧器の交流側の容量は$ \ 1 \ 000 \ \mathrm {[kV\cdot A]} \ $である。
$ \ X \ $で示すリアクトルは$ \ \fbox {　（１）　} \ $であり，これによって交流系統の短絡容量などの条件が交流フィルタ設備にあまり影響しないようにしている。このリアクトルのリアクタンスは，$ \ 1 \ 000 \ \mathrm {[kV\cdot A]} \ $を基準として$ \ 4 \ [％] \ $である。その1相当たりのインダクタンスは，$ \ \fbox {　（２）　} \ \mathrm {[mH]} \ $である。

$ \ 6 \ $パルスサイリスタ変換装置から発生する$ \ 5 \ $次及び$ \ \fbox {　（３）　} \ $の高調波は，$ \ 12 \ $パルスサイリスタ変換装置からは，理想的には発生しないが，実際には制御角のばらつきなどによってわずかに発生する。短絡容量が変換装置容量の数十倍で，インピーダンスが誘導性の一般的な系統条件では，第$ \ 11 \ $分路を接続することによってこれらの高調波の系統への流出が$ \ \fbox {　（４）　} \ $するので，これを防止するためにこれらの高調波に対する分路を設け，各分路の設備容量を第$ \ 5 \ $分路：$ \ 120 \ \mathrm {[kvar]} \ $，第$ \ \fbox {　（３）　} \ $分路：$ \ 80 \ \mathrm {[kvar]} \ $及び第$ \ 11 \ $分路：$ \ 200 \ \mathrm {[kvar]} \ $とした構成としている。

第$ \ 11 \ $分路のリアクトルの$ \ 1 \ $相当たりのインダクタンス$ \ L_{11} \ $は$ \ \fbox {　（５）　} \ \mathrm {[mH]} \ $である。

第$ \ 11 \ $分路は，$ \ 12 \ $パルス変換装置から発生する$ \ 11 \ $次の高調波電流だけでなく，それ以上の次数の高調波電流も吸収する。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　52.5　　　　　&（ロ）&　7　　　　　&（ハ）&　4.62 \\[ 5pt ] &（ニ）&　2.67　　　　　&（ホ）&　578　　　　　&（ヘ）&　8.01 \\[ 5pt ] &（ト）&　増　加　　　　　&（チ）&　4.81　　　　　&（リ）&　9 \\[ 5pt ] &（ヌ）&　分路リアクトル　　　　　　&（ル）&　限流リアクトル　　　　　　　&（ヲ）&　減　少 \\[ 5pt ] &（ワ）&　平均化　　　　　&（カ）&　共振リアクトル　　　　　&（ヨ）&　6
\end{eqnarray}
\]

【ワンポイント解説】

交流フィルタ設備に関する問題です。
$ \ 12 \ $パルスサイリスタ変換装置は$ \ 2 \ $種ではまず出題されないですが，$ \ 1 \ $種では二次試験でも出題される内容です。
計算力も重要ですが，メカニズムをしっかりと理解していることが最重要となります。

1.$ \ 12 \ $パルスサイリスタ変換装置
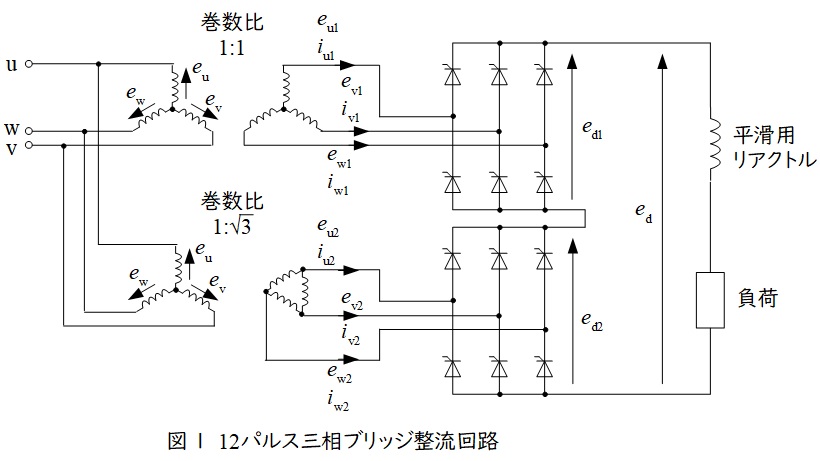
$ \ 12 \ $パルスサイリスタ変換装置の回路図を図1に示します。
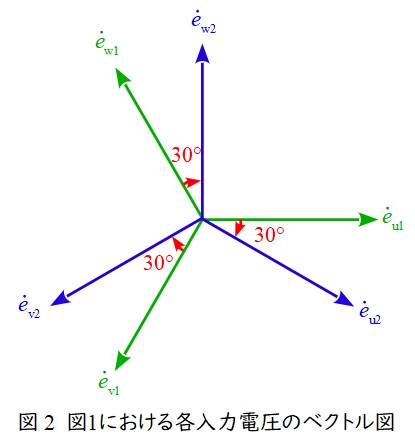
入力電圧を$ \ \mathrm {Y-Y} \ $接続と$ \ \mathrm {Y-\Delta } \ $接続に分け，巻数比を調整することにより，図2のように位相が$ \ 30° \ $ずれた入力電圧を取り出すことができます。
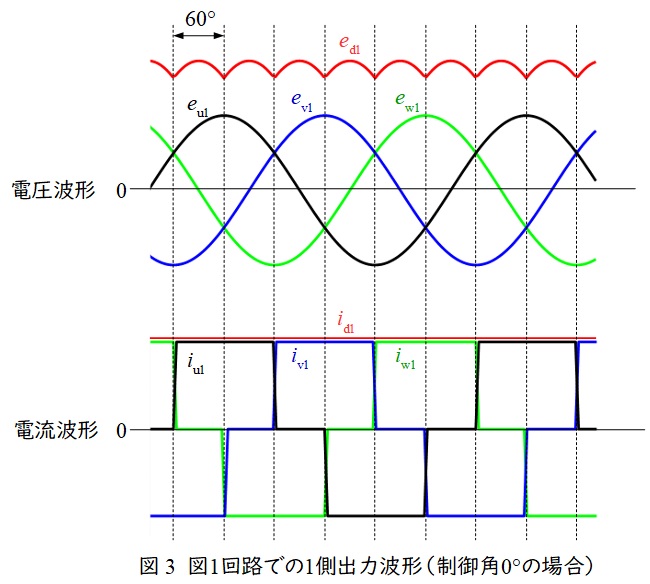
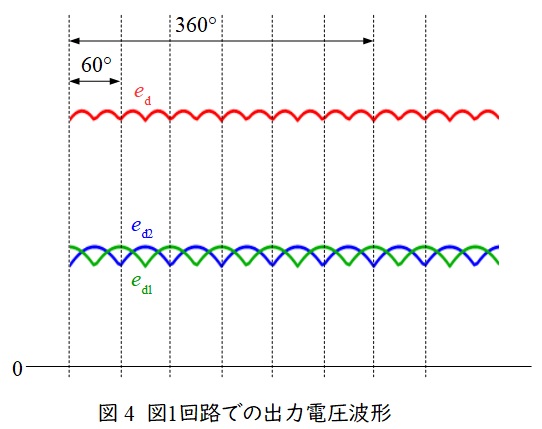
$ \ 1 \ $側の出力は図3のように$ \ 360° \ $の間に$ \ 6 \ $パルスの電圧$ \ e_{\mathrm {d1}} \ $を取り出すことができます。同様に$ \ 2 \ $側も$ \ 30° \ $ずれた$ \ 6 \ $パルスの電圧$ \ e_{\mathrm {d2}} \ $を取り出すことができるため，全体として，図4に示すような$ \ 12 \ $パルスの電圧を取り出すことができるようになります。
素子の切り替えのタイミングで高調波が発生するため，$ \ 12n± 1 \ $の高調波が発生します。

2.オーム法から単位法への変換
基準容量$ \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ $，基準電圧$ \ V_{\mathrm {n}} \ \mathrm {[V]} \ $，基準電流$ \ I_{\mathrm {n}} \ \mathrm {[A]} \ $の時，インピーダンス$ \ Z \ \mathrm {[\Omega ]} \ $を単位法で表すと，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ] &=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}}　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ル
題意より，「短絡容量等の条件が交流フィルタ設備にあまり影響しないように」という限流リアクトルそのものの説明となっています。

(2)解答：ハ
基準容量$ \ P_{\mathrm {B}} \ $，基準電圧$ \ V_{\mathrm {B}} \ $，基準電流$ \ I_{\mathrm {B}} \ $，基準インピーダンス$ \ X_{\mathrm {B}} \ $とすると単位法の定義から，
\[
\begin{eqnarray}
X_{\mathrm {B}}&=&\frac {V_{\mathrm {B}}}{\sqrt {3} I_{\mathrm {B}}} \\[ 5pt ] &=&\frac {V_{\mathrm {B}}^{2}}{P_{\mathrm {B}}} \\[ 5pt ] &=&\frac {6600^{2}}{1000 \times 10^{3}} \\[ 5pt ] &≒&43.56 \ [\Omega ] \\[ 5pt ] \end{eqnarray}
\] であるから，このリアクトルのリアクタンス$ \ X \ $は，
\[
\begin{eqnarray}
X&=&\frac {4}{100} \times 43.56 \\[ 5pt ] &=&1.7424 \ [\Omega ] \\[ 5pt ] \end{eqnarray}
\] となる。よって一相あたりインダクタンスを$ \ L \ $とすると，
\[
\begin{eqnarray}
X&=&2\pi fL \\[ 5pt ] L&=& \frac {X}{2 \pi f} \\[ 5pt ] &=&\frac {1.7424}{2 \pi \times 60} \\[ 5pt ] &≒&4.62\times 10^{-3} \ [\mathrm {H}]　→　4.62 \ [\mathrm {mH}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ロ
$ \ 6 \ $パルスサイリスタ変換装置からは$ \ 6n\pm 1 \ $の高調波が発生します。したがって，発生するのは$ \ 5 \ $次及び$ \ 7 \ $次の高調波になります。

(4)解答：ト
題意より，解答候補は（ト）増加，（ヲ）減少，（ワ）平均化，となると思います。（ト）増加以外ではその後の意味が繋がりませんので明らかに増加となります。
定量的には以下の通りとなります。
第$ \ 11 \ $分路フィルタのインダクタンスを$ \ L_{11} \ $，静電容量を$ \ C_{11} \ $とすると，共振条件は$ \ \omega=2 \pi f \ $とすれば，
\[
\begin{eqnarray}
11\omega L_{11}=\frac {1}{11\omega C_{11}} \\[ 5pt ] \frac {1}{\omega C_{11}}=121\omega L_{11} \\[ 5pt ] \end{eqnarray}
\] となる。
よってその$ \ 5 \ $次，$ \ 7 \ $次調波に対するリアクタンス$ \ X_{11-5} \ $，$ \ X_{11-7} \ $は，
\[
\begin{eqnarray}
X_{11-5}&=&\mathrm {j}5\omega L_{11}+\frac {1}{\mathrm {j}5\omega C_{11}} \\[ 5pt ] &=&\mathrm {j}5\omega L_{11}-\mathrm {j}\frac {121}{5}\omega L_{11} \\[ 5pt ] &=&-\mathrm {j}19.2\omega L_{11} \\[ 5pt ] X_{11-7}&=&\mathrm {j}7\omega L_{11}+\frac {1}{\mathrm {j}7\omega C_{11}} \\[ 5pt ] &=&\mathrm {j}7\omega L_{11}-\mathrm {j}\frac {121}{7}\omega L_{11} \\[ 5pt ] &≒&-\mathrm {j}10.29\omega L_{11} \\[ 5pt ] \end{eqnarray}
\] となる。よって，どちらも容量性のリアクタンスとなるので，高調波の系統への流出が増加する。

(5)解答：チ
第$ \ 11 \ $分路の設備容量が$ \ Q_{11}=200 \ \mathrm {[kvar]} \ $であるため，そのリアクタンス$ \ X_{11} \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
X_{11}&=&\frac {V_{\mathrm {B}}^{2}}{Q_{11}} \\[ 5pt ] &=&\frac {6600^{2}}{200 \times 10^{3}} \\[ 5pt ] &=&217.8 \ \mathrm {[\Omega ]}（容量性） \\[ 5pt ] \end{eqnarray}
\] となる。また，$ \ X_{11} \ $は，
\[
\begin{eqnarray}
X_{11}&=&\mathrm {j}\omega L_{11}+\frac {1}{\mathrm {j}\omega C_{11}} \\[ 5pt ] &=&\mathrm {j}\omega L_{11}-\mathrm {j}121\omega L_{11} \\[ 5pt ] &=&\mathrm {j}120\omega L_{11} \\[ 5pt ] \end{eqnarray}
\] となるので，両式から，
\[
\begin{eqnarray}
120\omega L_{11}&=&217.8 \\[ 5pt ] L_{11}&=&\frac {217.8}{120\omega} \\[ 5pt ] &=&\frac {217.8}{120\cdot 2\pi f} \\[ 5pt ] &=&\frac {217.8}{120\times 2\pi \times 60} \\[ 5pt ] &≒&4.81\times 10^{-3} \ \mathrm {[H]}　→　4.81 \ \mathrm {[mH]} \\[ 5pt ] \end{eqnarray}
\] と求められる。