【問題】
【難易度】★★★☆☆(普通)
次の文章は,配電線路における電力損失に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句,式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
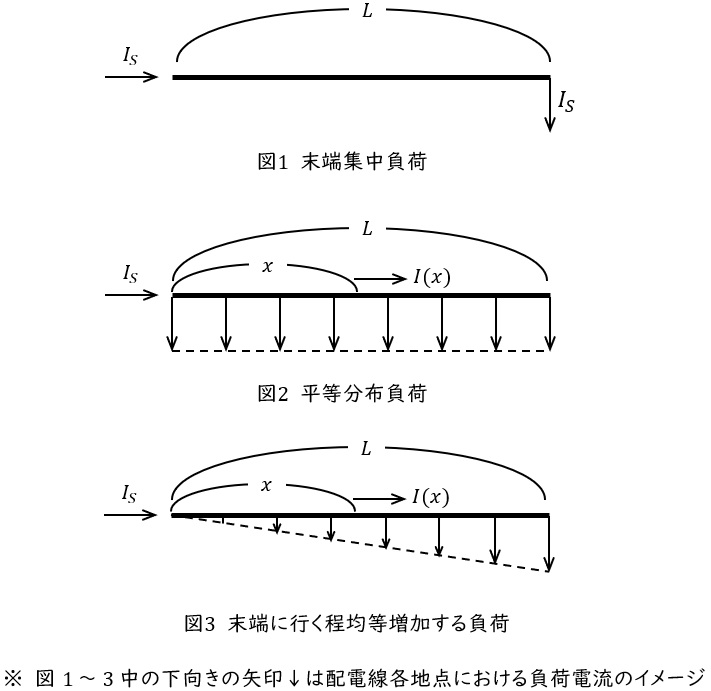
三相\( \ 3 \ \)線式配電線路で,図1のように負荷電流\( \ I_{S} \ \mathrm {[A]} \ \)が末端に集中している場合の電力損失は,線路の\( \ 1 \ \)線単位長当たりの抵抗を\( \ r \ \mathrm {[\Omega /m]} \ \),線路のこう長を\( \ L \ \mathrm {[m]} \ \)とすると\( \ \fbox { (1) } \ \mathrm {[W]} \ \)で表される。
図2のように,配電線の送電端電流(=負荷電流の総和)は図1の場合と同様に\( \ I_{S} \ \mathrm {[A]} \ \)であるが,負荷電流が線路の各地点において平等に分布している場合を考えると,送電端から\( \ x \ \mathrm {[m]} \ \)の地点における配電線の通過電流\( \ I(x) \ \mathrm {[A]} \ \)は\( \ \fbox { (2) } \ \)で表されるため,平等負荷分布線路の電力損失は,末端集中負荷線路の場合の\( \ \fbox { (3) } \ \)倍となる。
また,図3のように末端に行く程負荷が均等に増加する分布の場合,送電端から\( \ x \ \mathrm {[m]} \ \)の地点における配電線の通過電流\( \ I(x) \ \)は\( \ x \ \)の\( \ \fbox { (4) } \ \)の関数で表され,この場合の線路の電力損失は,末端集中負荷の場合の\( \ \fbox { (5) } \ \)倍となる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& 0.5 \ 乗 &(ロ)& 3I_{S}^{2}rL &(ハ)& 2 \ 乗 \\[ 5pt ]
&(ニ)& \left( 1+\frac {x}{L} \right) I_{S} &(ホ)& \frac {2}{3} &(ヘ)& \left( 1-\frac {x}{L} \right) I_{S} \\[ 5pt ]
&(ト)& \frac {1}{4} &(チ)& I_{S}^{2}rL &(リ)& \frac {8}{15} \\[ 5pt ]
&(ヌ)& 4 \ 乗 &(ル)& \frac {I_{S}^{2}rL}{3} &(ヲ)& \frac {1}{3} \\[ 5pt ]
&(ワ)& \frac {2}{15} &(カ)& \frac {x}{L} \cdot I_{S} &(ヨ)& \frac {1}{5} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
集中負荷,分布負荷の電力損失の比較に関する問題です。
\( \ 2 \ \)種の電力管理科目の定番となっている問題ですので解法の難易度自体は高くありませんが,電力科目の出題であるため,かなりの計算スピードが要求されています。
他の問題とのバランスも考えながら\( \ 20 \ \)分以内を目標に完答を目指すようにして下さい。
1.分布負荷の電力損失
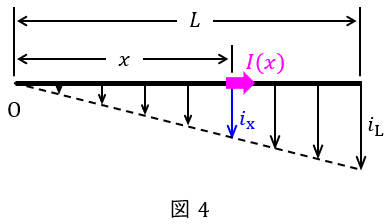
図4に示すような三相\( \ 3 \ \)線式配電線路において,線路のこう長\( \ L \ \mathrm {[m]} \ \),線路の\( \ 1 \ \)線の単位長さ当たりの抵抗\( \ r \ \mathrm {[\Omega /m]} \ \),リアクタンスを無視できるとし,末端の電流密度\( \ i_{\mathrm {L}} \ \mathrm {[A/m]} \ \)で,末端に行く程負荷が均等に増加する分布の負荷があるとします。
このとき,基準点\( \ \mathrm {O} \ \)から距離\( \ x \ \mathrm {[m]} \ \)の場所の電流密度\( \ i_{\mathrm {x}} \ \mathrm {[A/m]} \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {x}}&=&\frac {x}{L}i_{\mathrm {L}} \\[ 5pt ]
&=&\frac {i_{\mathrm {L}}}{L}x \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ x \ \mathrm {[m]} \ \)における配電線路の電流\( \ I(x) \ \mathrm {[A]} \ \)は,\( \ x \ \mathrm {[m]} \ \)から\( \ L \ \mathrm {[m]} \ \)までの電流密度の合計であるから,
\[
\begin{eqnarray}
I(x)&=&\int _{x}^{L}i_{\mathrm {x}}\mathrm {d}x \\[ 5pt ]
&=&\int _{x}^{L}\frac {i_{\mathrm {L}}}{L}x\mathrm {d}x \\[ 5pt ]
&=&\frac {i_{\mathrm {L}}}{L}\int _{x}^{L}x\mathrm {d}x \\[ 5pt ]
&=&\frac {i_{\mathrm {L}}}{L}\left[ \frac {x^{2}}{2}\right] _{x}^{L} \\[ 5pt ]
&=&\frac {i_{\mathrm {L}}}{L}\left( \frac {L^{2}}{2}-\frac {x^{2}}{2}\right) \\[ 5pt ]
&=&\frac {i_{\mathrm {L}}}{2L}\left( L^{2}-x^{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,基準点\( \ \mathrm {O} \ \)から距離\( \ x \ \mathrm {[m]} \ \)の場所の微小区間\( \ \mathrm {d}x \ \mathrm {[m]} \ \)での電力損失\( \ \mathrm {d}P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
\mathrm {d}P&=&3I(x)^{2}r\mathrm {d}x \\[ 5pt ]
&=&3\left\{ \frac {i_{\mathrm {L}}}{2L}\left( L^{2}-x^{2}\right) \right\} ^{2}r\mathrm {d}x \\[ 5pt ]
&=&\frac {3i_{\mathrm {L}}^{2}r}{4L^{2}}\left( L^{2}-x^{2}\right) ^{2}\mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
となり,配電線路全体の電力損失\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P&=&\int _{0}^{L}\frac {3i_{\mathrm {L}}^{2}r}{4L^{2}}\left( L^{2}-x^{2}\right) ^{2}\mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
で求められることになります。各式は暗記するのではなく,考え方を理解するようにしましょう。
【解答】
(1)解答:ロ
負荷電流\( \ I_{S} \ \mathrm {[A]} \ \)が末端に集中している場合,線路全体の抵抗\( \ R \ \mathrm {[\Omega]} \ \)は,
\[
\begin{eqnarray}
R&=&rL \\[ 5pt ]
\end{eqnarray}
\]
となるので,電力損失\( \ P_{1} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{1}&=&3I_{S}^{2}R \\[ 5pt ]
&=&3I_{S}^{2}rL \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヘ
負荷電流が平等に分布している場合,送電端から\( \ x \ \mathrm {[m]} \ \)の地点における電流密度\( \ i_{x} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
i_{x}&=&\frac {I_{S}}{L} \\[ 5pt ]
\end{eqnarray}
\]
であるから,送電端から\( \ x \ \mathrm {[m]} \ \)の地点における配電線の通過電流\( \ I(x) \ \mathrm {[A]} \ \)は,ワンポイント解説「1.分布負荷の電力損失」の通り,
\[
\begin{eqnarray}
I(x)&=&\int _{x}^{L}i_{\mathrm {x}}\mathrm {d}x \\[ 5pt ]
&=&\int _{x}^{L}\frac {I_{S}}{L}\mathrm {d}x \\[ 5pt ]
&=&\frac {I_{S}}{L}\int _{x}^{L}1\mathrm {d}x \\[ 5pt ]
&=&\frac {I_{S}}{L}\left[x \right] _{x}^{L} \\[ 5pt ]
&=&\frac {I_{S}}{L}\left( L-x \right) \\[ 5pt ]
&=&\frac {L-x}{L}I_{S} \\[ 5pt ]
&=&\left( 1-\frac {x}{L} \right) I_{S} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヲ
(2)解答式より,送電端から\( \ x \ \mathrm {[m]} \ \)の地点の微小区間\( \ \mathrm {d}x \ \mathrm {[m]} \ \)での電力損失\( \ \mathrm {d}P_{2} \ \mathrm {[W]} \ \)は,ワンポイント解説「1.分布負荷の電力損失」の通り,
\[
\begin{eqnarray}
\mathrm {d}P_{2}&=&3I(x)^{2}r\mathrm {d}x \\[ 5pt ]
&=&3\left\{ \left( 1-\frac {x}{L} \right) I_{S} \right\} ^{2}r\mathrm {d}x \\[ 5pt ]
&=&3I_{S}^{2}r\left( 1-\frac {x}{L}\right) ^{2}\mathrm {d}x \\[ 5pt ]
&=&3I_{S}^{2}r\left( 1-\frac {2}{L}x+\frac {1}{L^{2}}x^{2}\right) \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
となるので,配電線全体の電力損失\( \ P_{2} \ \mathrm {[W]} \ \)は,ワンポイント解説「1.分布負荷の電力損失」の通り,
\[
\begin{eqnarray}
P_{2}&=&\int _{0}^{L}3I_{S}^{2}r\left( 1-\frac {2}{L}x+\frac {1}{L^{2}}x^{2}\right) \mathrm {d}x \\[ 5pt ]
&=&3I_{S}^{2}r\int _{0}^{L}\left( 1-\frac {2}{L}x+\frac {1}{L^{2}}x^{2}\right) \mathrm {d}x \\[ 5pt ]
&=&3I_{S}^{2}r\left[ x-\frac {1}{L}x^{2}+\frac {1}{3L^{2}}x^{3}\right] _{0}^{L} \\[ 5pt ]
&=&3I_{S}^{2}r\left( L-\frac {1}{L}L^{2}+\frac {1}{3L^{2}}L^{3}\right) \\[ 5pt ]
&=&3I_{S}^{2}r\cdot \frac {L}{3} \\[ 5pt ]
&=&I_{S}^{2}Lr \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {P_{2}}{P_{1}} \ \)は,
\[
\begin{eqnarray}
\frac {P_{2}}{P_{1}}&=&\frac {I_{S}^{2}Lr}{3I_{S}^{2}rL } \\[ 5pt ]
&=&\frac {1}{3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
末端での電流密度を\( \ i_{L} \ \mathrm {[A]} \ \)とすると,送電端から\( \ x \ \mathrm {[m]} \ \)の地点における電流密度\( \ i_{x} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
i_{x}&=&\frac {x}{L}i_{L} \\[ 5pt ]
&=&\frac {i_{L}}{L}x \\[ 5pt ]
\end{eqnarray}
\]
となり,合計の電流値が\( \ I_{S} \ \mathrm {[A]} \ \)であるから,
\[
\begin{eqnarray}
I_{S}&=&\int _{0}^{L}i_{x} \mathrm {d}x \\[ 5pt ]
&=&\int _{0}^{L}\frac {i_{L}}{L}x \mathrm {d}x \\[ 5pt ]
&=&\frac {i_{L}}{L}\int _{0}^{L}x \mathrm {d}x \\[ 5pt ]
&=&\frac {i_{L}}{L}\left[ \frac {x^{2}}{2}\right] _{0}^{L} \\[ 5pt ]
&=&\frac {i_{L}}{L}\cdot \frac {L^{2}}{2} \\[ 5pt ]
&=&\frac {i_{L}L}{2} \\[ 5pt ]
i_{L}&=&\frac {2I_{S}}{L} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,電流密度\( \ i_{x} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
i_{x}&=&\frac {i_{L}}{L}x \\[ 5pt ]
&=&\frac {\displaystyle \frac {2I_{S}}{L} }{L}x \\[ 5pt ]
&=&\frac {2I_{S}}{L^{2}}x \\[ 5pt ]
\end{eqnarray}
\]
となるので,送電端から\( \ x \ \mathrm {[m]} \ \)の地点における配電線の通過電流\( \ I(x) \ \)は,
\[
\begin{eqnarray}
I(x)&=&\int _{x}^{L}i_{x} \mathrm {d}x \\[ 5pt ]
&=&\int _{x}^{L}\frac {2I_{S}}{L^{2}}x \mathrm {d}x \\[ 5pt ]
&=&\frac {2I_{S}}{L^{2}}\int _{x}^{L}x \mathrm {d}x \\[ 5pt ]
&=&\frac {2I_{S}}{L^{2}}\left[ \frac {x^{2}}{2}\right] _{x}^{L} \\[ 5pt ]
&=&\frac {2I_{S}}{L^{2}}\left( \frac {L^{2}}{2}-\frac {x^{2}}{2}\right) \\[ 5pt ]
&=&\frac {I_{S}}{L^{2}}\left( L^{2}-x^{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ I(x) \ \)は\( \ x \ \)の\( \ 2 \ \)乗の関数で表される。
(5)解答:リ
図3の条件における送電端から\( \ x \ \mathrm {[m]} \ \)の地点の微小区間\( \ \mathrm {d}x \ \mathrm {[m]} \ \)での電力損失\( \ \mathrm {d}P_{3} \ \mathrm {[W]} \ \)は,ワンポイント解説「1.分布負荷の電力損失」の通り,
\[
\begin{eqnarray}
\mathrm {d}P_{3}&=&3I(x)^{2}r\mathrm {d}x \\[ 5pt ]
&=&3\left\{ \frac {I_{S}}{L^{2}}\left( L^{2}-x^{2}\right) \right\} ^{2}r\mathrm {d}x \\[ 5pt ]
&=&\frac {3I_{S}^{2}r}{L^{4}}\left( L^{4}-2L^{2}x^{2}+x^{4}\right) \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
となるので,配電線全体の電力損失\( \ P_{3} \ \mathrm {[W]} \ \)は,ワンポイント解説「1.分布負荷の電力損失」の通り,
\[
\begin{eqnarray}
P_{3}&=&\int _{0}^{L}\frac {3I_{S}^{2}r}{L^{4}}\left( L^{4}-2L^{2}x^{2}+x^{4}\right) \mathrm {d}x \\[ 5pt ]
&=&\frac {3I_{S}^{2}r}{L^{4}}\int _{0}^{L}\left( L^{4}-2L^{2}x^{2}+x^{4}\right) \mathrm {d}x \\[ 5pt ]
&=&\frac {3I_{S}^{2}r}{L^{4}}\left[ L^{4}x-\frac {2}{3}L^{2}x^{3}+\frac {x^{5}}{5}\right] _{0}^{L} \\[ 5pt ]
&=&\frac {3I_{S}^{2}r}{L^{4}}\left( L^{5}-\frac {2}{3}L^{5}+\frac {L^{5}}{5}\right) \\[ 5pt ]
&=&\frac {3I_{S}^{2}r}{L^{4}}\cdot \frac {8}{15}L^{5} \\[ 5pt ]
&=&\frac {8}{5}I_{S}^{2}Lr \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {P_{3}}{P_{1}} \ \)は,
\[
\begin{eqnarray}
\frac {P_{3}}{P_{1}}&=&\frac {\displaystyle \frac {8}{5}I_{S}^{2}Lr}{3I_{S}^{2}rL } \\[ 5pt ]
&=&\frac {\displaystyle \frac {8}{5}}{3} \\[ 5pt ]
&=&\frac {8}{15} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん