【問題】
【難易度】★★★★★(難しい)
次の文章は, 長距離送電線路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
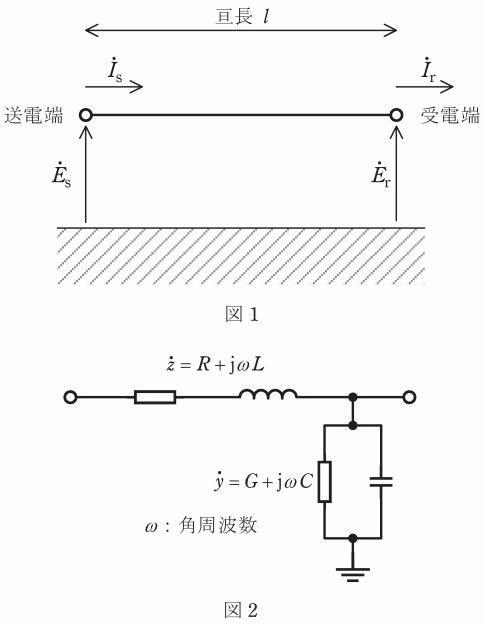
長距離送電線路は,線路定数が線路に沿って一様に分布した分布定数回路として考える必要がある。いま,図1に示す亘長\( \ l \ \)の送電線路において,送電線路単位長ごとの直列インピーダンス及び並列アドミタンスを図2のとおり表すとき,送電線の相電圧\( \ {\dot E}_{\mathrm {s}} \ \),電流\( \ {\dot I}_{\mathrm {s}} \ \)と受電端の相電圧\( \ {\dot E}_{\mathrm {r}} \ \),電流\( \ {\dot I}_{\mathrm {r}} \ \)の関係は,送電線路の四端子定数\( \ \dot A \ \),\( \ \dot B \ \),\( \ \dot C \ \),\( \ \dot D \ \)を用いて,次のとおり表すことができる。
\[
\begin{eqnarray}
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix}&=&\begin{bmatrix} \dot A & \dot B \\ \dot C & \dot D \end{bmatrix}\begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\dot A&=&\dot D= \ \fbox { (1) } \ \dot \gamma l \\[ 5pt ]
\dot B&=&{\dot Z}_{\mathrm {w}}\times \ \fbox { (2) } \ \dot \gamma l \\[ 5pt ]
\dot C&=&\frac {1}{{\dot Z}_{\mathrm {w}}}\times \ \fbox { (2) } \ \dot \gamma l \\[ 5pt ]
\end{eqnarray}
\]
ここに,定数\( \ \dot Z_{\mathrm {w}}=\sqrt {\dot z / \dot y} \ \)は\( \ \fbox { (3) } \ \),定数\( \ \dot \gamma=\sqrt {\dot z \dot y} \ \)は伝搬定数と呼ばれる。
次に,図2における抵抗分\( \ R \ \)とコンダクタンス分\( \ G \ \)は無視できるものとし,受電端において\( \ 1 \ \)相あたり有効電力\(\displaystyle \ P_{\mathrm {o}}=\frac {\left| {\dot E}_{\mathrm {r}}\right| ^{2}}{\left| {\dot Z}_{\mathrm {w}}\right| }=\frac {E_{\mathrm {r}}^{2}}{\sqrt {L / C}} \ \)(但し,力率は\( \ 1 \ \)とし,\( \ E_{\mathrm {r}} \ \)は受電端電圧\( \ {\dot E}_{\mathrm {r}} \ \)の大きさを表す。)を受電する場合の送電端電圧\( \ {\dot E}_{\mathrm {s}} \ \)の大きさ\( \ E_{\mathrm {s}} \ \)を求めると,\( \ E_{\mathrm {s}}= \ \fbox { (4) } \ \)となる。この状態から,受電する有効電力を減少させた場合,受電端電圧は送電端電圧に対して\( \ \fbox { (5) } \ \)。このような特徴があることから,\( \ P_{\mathrm {o}} \ \)を\( \ 3 \ \)相分合計した値(固有送電容量と呼ばれる。)は,長距離送電線路の特性を把握するうえで重要な値である。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 伝搬インピーダンス &(ロ)& \sinh &(ハ)& 低下する \\[ 5pt ]
&(ニ)& 漸近する &(ホ)& 特性インピーダンス &(ヘ)& \tan \\[ 5pt ]
&(ト)& E_{\mathrm {r}}\left( 1+\tanh \omega \sqrt {LC}\right) &(チ)& \tanh &(リ)& \cos \\[ 5pt ]
&(ヌ)& \sin &(ル)& 線路インピーダンス &(ヲ)& 上昇する \\[ 5pt ]
&(ワ)& \cosh &(カ)& E_{\mathrm {r}}\left( 1+\tan \omega \sqrt {LC}\right) &(ヨ)& E_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
分布定数回路に関する問題で,ほとんどの受験生が苦戦を強いられたのではないかと思います。分布定数回路の式は導出は可能ですが,計算が非常に長くなるため,基本的には試験では覚えておくことが必要です。
1.分布定数回路の送電端電圧・電流と受電端電圧・電流の関係
長距離送電線では線路の特性インピーダンスや伝搬定数を無視することはできず,分布定数回路として扱います。線路の特性インピーダンスを\({\dot Z}_{\mathrm {w}}\),伝搬定数を\(\dot \gamma \),線路の長さを\(l\)とすると,
\[
\begin{eqnarray}
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} &=& \begin{bmatrix} \cosh \dot \gamma l & {\dot Z}_{\mathrm {w}}\sinh \dot \gamma l \\ \displaystyle \frac {1}{{\dot Z}_{\mathrm {w}}}\sinh \dot \gamma l & \cosh \dot \gamma l \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.双曲線関数
\( \ \sinh \dot \gamma l \ \)や\( \ \cosh \dot \gamma l \ \)は双曲線関数と呼ばれ,
\[
\begin{eqnarray}
\sinh \dot \gamma l &=& \frac {\mathrm {e}^{\dot \gamma l }-\mathrm {e}^{-\dot \gamma l }}{2} \\[ 5pt ]
\cosh \dot \gamma l &=& \frac {\mathrm {e}^{\dot \gamma l }+\mathrm {e}^{-\dot \gamma l }}{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ \dot \gamma =\mathrm {j}\beta \ \)の場合,
\[
\begin{eqnarray}
\sinh \mathrm {j}\beta l&=& \frac {\mathrm {e}^{\mathrm {j}\beta l}-\mathrm {e}^{-\mathrm {j}\beta l}}{2} \\[ 5pt ]
&=& \frac {\cos \beta l+\mathrm {j}\sin \beta l-\left( \cos \beta l-\mathrm {j}\sin \beta l \right) }{2} \\[ 5pt ]
&=&\mathrm {j}\sin \beta l \\[ 5pt ]
\cosh \mathrm {j}\beta l&=& \frac {\mathrm {e}^{\mathrm {j}\beta l}+\mathrm {e}^{-\mathrm {j}\beta l}}{2} \\[ 5pt ]
&=& \frac {\cos \beta l+\mathrm {j}\sin \beta l+ \cos \beta l-\mathrm {j}\sin \beta l}{2} \\[ 5pt ]
&=&\cos \beta l \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ワ
ワンポイント解説「1.分布定数回路の送電端電圧・電流と受電端電圧・電流の関係」の通り,\( \ \dot A \ \)及び\( \ \dot D \ \)は\( \ \cosh \dot \gamma l \ \)となります。
(2)解答:ロ
ワンポイント解説「1.分布定数回路の送電端電圧・電流と受電端電圧・電流の関係」の通り,\( \ \dot B \ \)は\( \ {\dot Z}_{\mathrm {w}}\sinh \dot \gamma l \ \),\( \ \dot C \ \)は\( \ \displaystyle \frac {1}{{\dot Z}_{\mathrm {w}}}\sinh \dot \gamma l \ \)となります。
(3)解答:ホ
ワンポイント解説「1.分布定数回路の送電端電圧・電流と受電端電圧・電流の関係」の通り,\( \ {\dot Z}_{\mathrm {w}} \ \)は特性インピーダンスと言います。
(4)解答:ヨ
行列式より,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=& {\dot E}_{\mathrm {r}} \cosh \dot \gamma l + {\dot I}_{\mathrm {r}}{\dot Z}_{\mathrm {w}}\sinh \dot \gamma l \\[ 5pt ]
{\dot I}_{\mathrm {s}} &=& {\dot E}_{\mathrm {r}} \frac {1}{{\dot Z}_{\mathrm {w}}}\sinh \dot \gamma l + {\dot I}_{\mathrm {r}}\cosh \dot \gamma l \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より,\( \ 1 \ \)相あたり有効電力\(\displaystyle \ \frac {\left| {\dot E}_{\mathrm {r}}\right| ^{2}}{\left| {\dot Z}_{\mathrm {w}}\right| }=\frac {E_{\mathrm {r}}^{2}}{\sqrt {L / C}} \ \)の抵抗負荷であるから,\( \ {\dot E}_{\mathrm {r}} ={\dot Z}_{\mathrm {w}}{\dot I}_{\mathrm {r}} \ \)の関係があるため,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=& {\dot E}_{\mathrm {r}} \cosh \dot \gamma l + {\dot E}_{\mathrm {r}} \sinh \dot \gamma l \\[ 5pt ]
{\dot I}_{\mathrm {s}} &=& {\dot I}_{\mathrm {r}}\sinh \dot \gamma l + {\dot I}_{\mathrm {r}}\cosh \dot \gamma l \\[ 5pt ]
\end{eqnarray}
\]
となる。それぞれ変形すると,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=& {\dot E}_{\mathrm {r}} \cdot \frac {\mathrm {e}^{\dot \gamma l }+\mathrm {e}^{-\dot \gamma l }}{2} + {\dot E}_{\mathrm {r}} \cdot \frac {\mathrm {e}^{\dot \gamma l }-\mathrm {e}^{-\dot \gamma l }}{2} \\[ 5pt ]
&=& {\dot E}_{\mathrm {r}} \mathrm {e}^{\dot \gamma l } \\[ 5pt ]
{\dot I}_{\mathrm {s}} &=& {\dot I}_{\mathrm {r}}\cdot \frac {\mathrm {e}^{\dot \gamma l }-\mathrm {e}^{-\dot \gamma l }}{2} + {\dot I}_{\mathrm {r}}\cdot \frac {\mathrm {e}^{\dot \gamma l }+\mathrm {e}^{-\dot \gamma l }}{2} \\[ 5pt ]
&=& {\dot I}_{\mathrm {r}}\mathrm {e}^{\dot \gamma l } \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \dot \gamma = \sqrt {\mathrm {j}\omega L \cdot \mathrm {j}\omega C }=\mathrm {j}\omega \sqrt {LC} \ \)であるから,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=& {\dot E}_{\mathrm {r}} \mathrm {e}^{\mathrm {j} \omega \sqrt {LC} l } \\[ 5pt ]
{\dot I}_{\mathrm {s}} &=& {\dot I}_{\mathrm {r}} \mathrm {e}^{\mathrm {j} \omega \sqrt {LC} l } \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,送電端1相あたりの有効電力\( \ P_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {s}} &=& \mathrm {Re} ( {\dot E}_{\mathrm {s}}\overline {{\dot I}_{\mathrm {s}}} ) \\[ 5pt ]
&=& \mathrm {Re} ( {\dot E}_{\mathrm {r}} \mathrm {e}^{\mathrm {j} \omega \sqrt {LC} l }{\dot I}_{\mathrm {r}} \mathrm {e}^{-\mathrm {j} \omega \sqrt {LC} l } ) \\[ 5pt ]
&=& \mathrm {Re} ( {\dot E}_{\mathrm {r}}{\dot I}_{\mathrm {r}} ) \\[ 5pt ]
&=& \mathrm {Re} ( {\dot E}_{\mathrm {r}}\frac {{\dot E}_{\mathrm {r}}}{{\dot Z}_{\mathrm {w}}} ) \\[ 5pt ]
&=& \frac {\left| {\dot E}_{\mathrm {r}}\right| ^{2}}{\left| {\dot Z}_{\mathrm {w}}\right| } \\[ 5pt ]
\end{eqnarray}
\]
となる。送電線は無損失回路であるから,\( \ P_{\mathrm {s}}=P_{\mathrm {o}} \ \)であるため,\( \ {\dot E}_{\mathrm {s}}={\dot E}_{\mathrm {r}} \ \)となる。
(5)解答:ヲ
行列式より,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=& {\dot E}_{\mathrm {r}} \cosh \dot \gamma l + {\dot I}_{\mathrm {r}}{\dot Z}_{\mathrm {w}}\sinh \dot \gamma l \\[ 5pt ]
&=& {\dot E}_{\mathrm {r}} \cosh \mathrm {j}\omega \sqrt {LC} l + {\dot I}_{\mathrm {r}}{\dot Z}_{\mathrm {w}}\sinh \mathrm {j}\omega \sqrt {LC} l \\[ 5pt ]
&=& {\dot E}_{\mathrm {r}} \cos \omega \sqrt {LC} l + \mathrm {j}{\dot I}_{\mathrm {r}}{\dot Z}_{\mathrm {w}}\sin \omega \sqrt {LC} l \\[ 5pt ]
\end{eqnarray}
\]
となる。受電する有効電力を減少させると,受電端電圧は送電端電圧に対して上昇する。例えば上式において,\( \ {\dot I}_{\mathrm {r}}→0 \ \)としていくと,送電端電圧は,\( \ {\dot E}_{\mathrm {s}}≒{\dot E}_{\mathrm {r}} \cos \omega \sqrt {LC} l \ \)となり,\( \ \cos \omega \sqrt {LC} l<1 \ \)とであるため,送電端電圧は受電端電圧よりも低くなる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん