【問題】
【難易度】★★★★★(難しい)
よくねん架された三相送電線\( \ 1 \ \)回線とタップ付き変圧器からなる送電系統がある。図に示すように,送電線は\( \ \mathrm {T} \ \)型等価回路で表され,そのインピーダンスを\( \ \dot Z \ \mathrm {[p.u.]} \ \),アドミタンスを\( \ \dot Y \ \mathrm {[p.u.]} \ \),タップ付き変圧器はタップ比を\( \ 1:n \ \)とし,漏れインピーダンスを\( \ \dot X \ \mathrm {[p.u.]} \ \)とする。送電線及びタップ付き変圧器の抵抗は無視でき,送電端の電圧\( \ {\dot V}_{s} \ \)は大きさが常に\( \ 1.00 \ \mathrm {[p.u.]} \ \)に保たれているものとする。
次の問に答えよ。なお,単位はすべて単位法の\( \ \mathrm {[p.u.]} \ \)とする。
(1) タップ比\( \ n \ \)を\( \ 1.05 \ \)とし,受電端を開放したとき,受電端電圧\( \ {\dot V}_{r} \ \)及び送電端電流\( \ {\dot I}_{s} \ \)の大きさはそれぞれ\( \ 1.13 \ \mathrm {[p.u.]} \ \)及び\( \ 0.39 \ \mathrm {[p.u.]} \ \)(進み)であった。次に受電端を短絡したとき,受電端電流\( \ {\dot I}_{r} \ \)の大きさは\( \ 1.88 \ \mathrm {[p.u.]} \ \)(遅れ)であった。この送電系統の四端子定数\( \ \dot A \ \),\( \ \dot B \ \),\( \ \dot C \ \)及び\( \ \dot D \ \)を求めよ。
(2) このとき,\( \ \dot Z \ \),\( \ \dot Y \ \)及び\( \ \dot X \ \)の値\( \ \mathrm {[p.u.]} \ \)はいくつか。
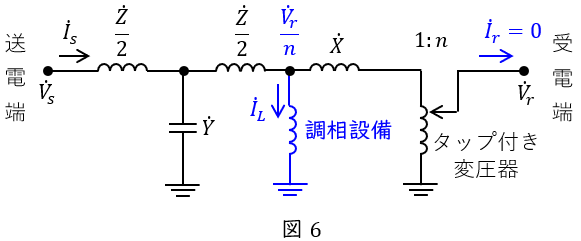
(3) 次にタップ比\( \ n \ \)を\( \ 0.95 \ \)に変更し,受電端を開放したとき,受電端の電圧が\( \ 1.00 \ \mathrm {[p.u.]} \ \)となるように適切な容量の調相設備をタップ付き変圧器の一次側(送電線側)に並列に入れた。この調相設備に流れ込む無効電力\( \ \mathrm {[p.u.]} \ \)(遅れ)を求めよ。
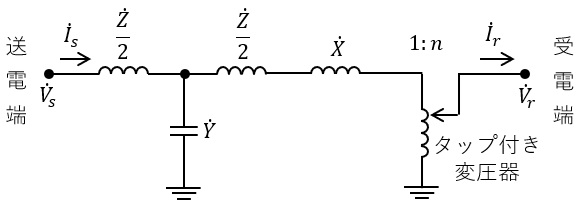
【ワンポイント解説】
タップ付き変圧器を含む四端子定数に関する問題です。
練習問題としては非常に良い問題ですが,計算量が非常に多いため,試験本番では選択しない方が良い問題かと思います。
二次試験では語群等もないため,計算間違いに注意して,丁寧に解いていくようにして下さい。
1.四端子定数
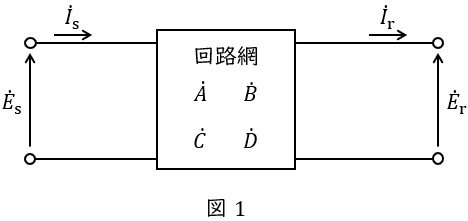
任意の図1のような回路がある時,送電端の相電圧\( \ {\dot E}_{\mathrm {s}} \ \)と電流\( \ {\dot I}_{\mathrm {s}} \ \),受電端の相電圧\( \ {\dot E}_{\mathrm {r}} \ \)と電流\( \ {\dot I}_{\mathrm {r}} \ \)の関係が以下の行列で表されるものを四端子定数と言います。
\[
\begin{eqnarray}
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} = \begin{bmatrix} \dot A & \dot B \\ \dot C & \dot D \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix}
\end{eqnarray}
\]
ただし,
\[
\begin{eqnarray}
\dot A&=&\left. \frac {{\dot E}_{\mathrm {s}}}{{\dot E}_{\mathrm {r}}} \right| _{{\dot I}_{\mathrm {r}}=0}
\dot B&=&\left. \frac {{\dot E}_{\mathrm {s}}}{{\dot I}_{\mathrm {r}}} \right| _{{\dot E}_{\mathrm {r}}=0} \\[ 5pt ]
\dot C&=&\left. \frac {{\dot I}_{\mathrm {s}}}{{\dot E}_{\mathrm {r}}} \right| _{{\dot I}_{\mathrm {r}}=0}
\dot D&=&\left. \frac {{\dot I}_{\mathrm {s}}}{{\dot I}_{\mathrm {r}}} \right| _{{\dot E}_{\mathrm {r}}=0}
\end{eqnarray}
\]
また,詳細は専門性が高いため割愛しますが,線形受動素子である抵抗やコイル,コンデンサで構成される相反回路であるとき,四端子定数は,
\[
\begin{eqnarray}
\dot A\dot D-\dot B\dot C&=&1 \\[ 5pt ]
\end{eqnarray}
\]
が成立します。
2.代表的な四端子定数
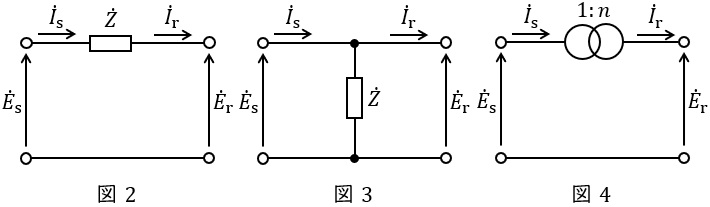
図2~図4の四端子定数は以下の通りとなります。
①図2
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&{\dot E}_{\mathrm {r}}+\dot Z {\dot I}_{\mathrm {r}} \\[ 5pt ]
{\dot I}_{\mathrm {s}}&=&{\dot I}_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,行列式の形にすると,
\[
\begin{eqnarray}
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} &=& \begin{bmatrix} 1 & \dot Z \\ 0 & 1 \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix} → \begin{bmatrix} 1 & \dot Z \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
②図3
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&{\dot E}_{\mathrm {r}} \\[ 5pt ]
{\dot I}_{\mathrm {s}}&=&\frac {1}{\dot Z}{\dot E}_{\mathrm {r}}+{\dot I}_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,行列式の形にすると,
\[
\begin{eqnarray}
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} &=& \begin{bmatrix} 1 & 0 \\ \displaystyle \frac {1}{\dot Z} & 1 \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix} → \begin{bmatrix} 1 & 0 \\ \displaystyle \frac {1}{\dot Z} & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
③図4
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&\frac {1}{n}{\dot E}_{\mathrm {r}} \\[ 5pt ]
{\dot I}_{\mathrm {s}}&=&n{\dot I}_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,行列式の形にすると,
\[
\begin{eqnarray}
\begin{bmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{bmatrix} &=& \begin{bmatrix} \displaystyle \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} \begin{bmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{bmatrix} → \begin{bmatrix} \displaystyle \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)送電系統の四端子定数
送電線及びタップ付き変圧器の抵抗は無視できるとなっていることから,電圧の位相角を基準をすると,電流は純虚数で表されることになる。したがって,受電端を開放\( \ \left( {\dot I}_{r}=0 \ \mathrm {[p.u.]}\right) \ \)としたとき,
\[
\begin{eqnarray}
{\dot V}_{s}&=&1.00 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot I}_{s}&=&j0.39 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot V}_{r}&=&1.13 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,四端子定数の\( \ \dot A \ \)と\( \ \dot C \ \)は,
\[
\begin{eqnarray}
\dot A&=&\frac {{\dot V}_{s}}{{\dot V}_{r}} \\[ 5pt ]
&=&\frac {1.00}{1.13} \\[ 5pt ]
&≒&0.884 \ 96 → 0.885 \\[ 5pt ]
\dot C&=&\frac {{\dot I}_{s}}{{\dot V}_{r}} \\[ 5pt ]
&=&\frac {j0.39}{1.13} \\[ 5pt ]
&=&j0.345 \ 13 → j0.345 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,受電端を短絡\( \ \left( {\dot V}_{r}=0 \ \mathrm {[p.u.]}\right) \ \)としたとき,
\[
\begin{eqnarray}
{\dot V}_{s}&=&1.00 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot I}_{r}&=&-j1.88 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,四端子定数の\( \ \dot B \ \)は,
\[
\begin{eqnarray}
\dot B&=&\frac {{\dot V}_{s}}{{\dot I}_{r}} \\[ 5pt ]
&=&\frac {1.00}{-j1.88} \\[ 5pt ]
&≒&j0.531 \ 91 → j0.532 \\[ 5pt ]
\end{eqnarray}
\]
となる。また,\( \ \dot A\dot D-\dot B\dot C=1 \ \)が成立することから,
\[
\begin{eqnarray}
\dot D&=&\frac {1+\dot B\dot C}{\dot A} \\[ 5pt ]
&=&\frac {1+j0.531 \ 91\times j0.345 \ 13}{0.884 \ 96} \\[ 5pt ]
&≒&0.922 \ 55 → 0.923 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ \dot Z \ \),\( \ \dot Y \ \)及び\( \ \dot X \ \)の値\( \ \mathrm {[p.u.]} \ \)
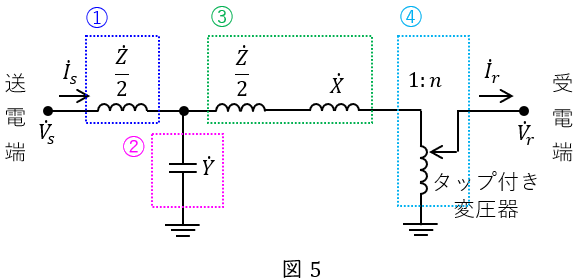
問題に与えられている送電系統を図5のように4つに分けると,それぞれの四端子係数は,
①
\[
\begin{eqnarray}
\begin{bmatrix} 1 & \displaystyle \frac {\dot Z}{2} \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
②
\[
\begin{eqnarray}
\begin{bmatrix} 1 & 0 \\ \dot Y & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
③
\[
\begin{eqnarray}
\begin{bmatrix} 1 & \displaystyle \frac {\dot Z}{2}+\dot X \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
④
\[
\begin{eqnarray}
\begin{bmatrix} \displaystyle \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,送電系統全体の四端子係数は,
\[
\begin{eqnarray}
\begin{bmatrix} \dot A & \dot B \\ \dot C & \dot D \end{bmatrix} &=&\begin{bmatrix} 1 & \displaystyle \frac {\dot Z}{2} \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 \\ \dot Y & 1 \end{bmatrix}\begin{bmatrix} 1 & \displaystyle \frac {\dot Z}{2}+\dot X \\ 0 & 1 \end{bmatrix}\begin{bmatrix} \displaystyle \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} 1+\displaystyle \frac {\dot Z\dot Y}{2} & \displaystyle \frac {\dot Z}{2} \\ \dot Y & 1 \end{bmatrix}\begin{bmatrix} 1 & \displaystyle \frac {\dot Z}{2}+\dot X \\ 0 & 1 \end{bmatrix}\begin{bmatrix} \displaystyle \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} 1+\displaystyle \frac {\dot Z\dot Y}{2} & \displaystyle \frac {\dot Z}{2}\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) +\dot X\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) +\frac {\dot Z}{2} \\ \dot Y & \displaystyle \frac {\dot Z\dot Y}{2}+\dot X\dot Y+1 \end{bmatrix}\begin{bmatrix} \displaystyle \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} 1+\displaystyle \frac {\dot Z\dot Y}{2} & \displaystyle \dot Z\left( 1+\displaystyle \frac {\dot Z\dot Y}{4}\right) +\dot X\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) \\ \dot Y & \displaystyle 1+\frac {\dot Z\dot Y}{2}+\dot X\dot Y \end{bmatrix}\begin{bmatrix} \displaystyle \frac {1}{n} & 0 \\ 0 & n \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} \displaystyle \frac {1}{n}\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) & \displaystyle n\dot Z\left( 1+\displaystyle \frac {\dot Z\dot Y}{4}\right) +n\dot X\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) \\ \displaystyle \frac {1}{n}\dot Y & \displaystyle n\left( 1+\frac {\dot Z\dot Y}{2}\right) +n\dot X\dot Y \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)より,\( \ \dot C=j0.345 \ 13 \ \)であるから,
\[
\begin{eqnarray}
\dot C &=&\frac {1}{n}\dot Y \\[ 5pt ]
\dot Y &=&n\dot C \\[ 5pt ]
&=&1.05\times j0.345 \ 13 \\[ 5pt ]
&≒&j0.362 \ 39 → j0.362 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \dot A=0.884 \ 96 \ \)であるから,
\[
\begin{eqnarray}
\dot A &=&\frac {1}{n}\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) \\[ 5pt ]
1+\displaystyle \frac {\dot Z\dot Y}{2} &=&n\dot A \\[ 5pt ]
\frac {\dot Z\dot Y}{2} &=&n\dot A -1 \\[ 5pt ]
\dot Z&=&\frac {2}{\dot Y}\left( n\dot A -1\right) \\[ 5pt ]
&=&\frac {2}{j0.362 \ 39}\times \left( 1.05 \times 0.884 \ 96 -1\right) \\[ 5pt ]
&≒&j0.390 \ 70 → j0.391 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。さらに,\( \ \dot D=0.922 \ 55 \ \)であるから,
\[
\begin{eqnarray}
\dot D &=&n\left( 1+\frac {\dot Z\dot Y}{2}\right) +n\dot X\dot Y \\[ 5pt ]
n\dot X\dot Y &=&\dot D-n\left( 1+\frac {\dot Z\dot Y}{2}\right) \\[ 5pt ]
\dot X &=&\frac {1}{n\dot Y}\left\{ \dot D-n\left( 1+\frac {\dot Z\dot Y}{2}\right) \right\} \\[ 5pt ]
&=&\frac {1}{1.05\times j0.362 \ 39}\times \left\{ 0.922 \ 55-1.05\times \left( 1+\frac {j0.390 \ 70\times j0.362 \ 39}{2}\right) \right\} \\[ 5pt ]
&≒&j0.139 \ 60 → j0.140 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)調相設備に流れ込む無効電力\( \ \mathrm {[p.u.]} \ \)(遅れ)
題意に沿って図を描くと図6のようになる。
(2)と同様に送電端から変圧器一次側までの四端子係数は,
\[
\begin{eqnarray}
\begin{bmatrix} \dot A & \dot B \\ \dot C & \dot D \end{bmatrix} &=&\begin{bmatrix} 1 & \displaystyle \frac {\dot Z}{2} \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 \\ \dot Y & 1 \end{bmatrix}\begin{bmatrix} 1 & \displaystyle \frac {\dot Z}{2} \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix} 1+\displaystyle \frac {\dot Z\dot Y}{2} & \displaystyle \dot Z\left( 1+\displaystyle \frac {\dot Z\dot Y}{4}\right) \\ \dot Y & \displaystyle 1+\frac {\dot Z\dot Y}{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,調相設備に流れる電流を\( \ {\dot I}_{L} \ \mathrm {[p.u.]} \ \)とすれば,
\[
\begin{eqnarray}
\begin{bmatrix} {\dot V}_{s} \\ {\dot I}_{s} \end{bmatrix} &=& \begin{bmatrix} 1+\displaystyle \frac {\dot Z\dot Y}{2} & \displaystyle \dot Z\left( 1+\displaystyle \frac {\dot Z\dot Y}{4}\right) \\ \dot Y & \displaystyle 1+\frac {\dot Z\dot Y}{2} \end{bmatrix}\begin{bmatrix} \displaystyle \frac {{\dot V}_{r}}{n} \\ {\dot I}_{L} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ {\dot I}_{L} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{s} &=& \left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) \frac {{\dot V}_{r}}{n}+ \dot Z\left( 1+\displaystyle \frac {\dot Z\dot Y}{4}\right) {\dot I}_{L} \\[ 5pt ]
\dot Z\left( 1+\displaystyle \frac {\dot Z\dot Y}{4}\right) {\dot I}_{L} &=& {\dot V}_{s}-\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) \frac {{\dot V}_{r}}{n} \\[ 5pt ]
{\dot I}_{L} &=& \frac {{\dot V}_{s}-\left( 1+\displaystyle \frac {\dot Z\dot Y}{2}\right) \displaystyle \frac {{\dot V}_{r}}{n}}{\displaystyle \dot Z\left( 1+\displaystyle \frac {\dot Z\dot Y}{4}\right) } \\[ 5pt ]
&=& \frac {1.00-\left( 1+\displaystyle \frac {j0.390 \ 70\times j0.362 \ 39}{2}\right) \times \displaystyle \frac {1.00}{0.95}}{\displaystyle j0.390 \ 70\times \left( 1+\displaystyle \frac {j0.390 \ 70\times j0.362 \ 39}{4}\right) } \\[ 5pt ]
&≒& \frac {0.021 \ 887}{j0.376 \ 87} \\[ 5pt ]
&≒& -j0.058 \ 076 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,調相設備に流れ込む無効電力\( \ {\dot Q}_{L} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot Q}_{L} &=&\left| \frac {{\dot V}_{r}}{n} {\dot I}_{L} \right| \\[ 5pt ]
&=& \frac {1.00}{0.95}\times 0.058 \ 076 \\[ 5pt ]
&≒& 0.061 \ 1 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん