【問題】
【難易度】★★☆☆☆(やや易しい)
図のような特別高圧系統と連系している風力発電所があり,風速の変化による出力変動のため,系統に電圧フリッカが生じることがある。風力発電所の出力が無負荷から最大出力まで変動する場合の電圧変動について,次の問に答えよ。ただし,発電所の最大出力は\( \ 60 \ 000 \ \mathrm {[kW]} \ \),系統の変圧器及び送電線のインピーダンスは図で示した\( \ \mathrm {p.u.} \ \)値(基準電力\( \ 100 \ \mathrm {[MV\cdot A]} \ \))とし,示した以外のインピーダンスや,他の負荷電力などの影響は無視できるものとする。また,上位系統側母線の電圧は\( \ 1.0 \ \mathrm {[p.u.]} \ \)で一定に保たれているものとする。
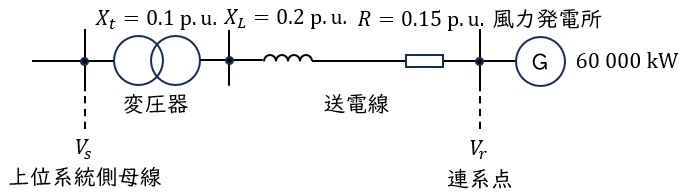
(1) 線路(変圧器及び送電線)の抵抗分が\( \ R \ \mathrm {[p.u.]} \ \),リアクタンス分が\( \ X \ \mathrm {[p.u.]} \ \)の場合で,発電所から線路に流れる有効電力を\( \ P \ \mathrm {[p.u.]} \ \)(連系点から線路方向を正とする。), 無効電力を\( \ Q \ \mathrm {[p.u.]} \ \)(遅れを正とする。)としたとき,連系点の電圧\( \ V_{r} \ \mathrm {[p.u.]} \ \)を\( \ R \ \),\( \ X \ \),\( \ P \ \),\( \ Q \ \)からなる簡易な式で求めよ。
なお,上位系統側母線の電圧\( \ V_{s} \ \)と電圧\( \ V_{r} \ \)との位相角差は小さく,\( \ V_{s} \ \)と\( \ V_{r} \ \)は同位相とみなせるものとして計算し,計算過程において必要な場合は次の近似式を用いること。
\[
\begin{eqnarray}
\sqrt {1+4\left( RP+XQ\right) } &≒& 1+2\left( RP+XQ\right) \\[ 5pt ]
\end{eqnarray}
\]
(2) 連系点での風力発電所の力率を\( \ 100 \ \mathrm {[%]} \ \)一定で運転した場合,連系点の電圧変動率\( \ \mathrm {[%]} \ \)を求めよ。なお,電圧値は,上記(1)で得られた式に,図のインピーダンスと発電電力の値を代入して計算すること。
(3) 風力発電所を一定力率で進相運転した場合,連系点での電圧変動率を\( \ 2.0 \ \mathrm {[%]} \ \)とするための連系点での風力発電所の運転力率\( \ \mathrm {[%]} \ \)を求めよ。なお,電圧値は,上記(1)で得られた式に,図のインピーダンスと発電電力の値を代入して計算すること。ただし,連系点の電圧は\( \ 1.0 \ \mathrm {[p.u.]} \ \)を下回らないこととする。
【ワンポイント解説】
風力発電所連系時の電圧変動率を考える問題です。
逆潮流であることが少し受験生を惑わす問題ですが,基本的な考え方は変わりません。
単位法の扱いに十分に注意して完答を目指すようにして下さい。
1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時,インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.単位法のおける電力
三相線路において,送電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \),受電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \),送電線電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3{\dot E}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
ここで,基準容量を\( P_{\mathrm {n}}=3E_{\mathrm {n}}I_{\mathrm {n}} \ \)としたとき,単位法での複素電力は,
\[
\begin{eqnarray}
\frac {P}{3E_{\mathrm {n}}I_{\mathrm {n}}}+\mathrm {j}\frac {Q}{3E_{\mathrm {n}}I_{\mathrm {n}}}&=&\frac {3{\dot E}_{\mathrm {r}}\overline {\dot I}}{3E_{\mathrm {n}}I_{\mathrm {n}}} \\[ 5pt ]
\frac {P}{P_{\mathrm {n}}}+\mathrm {j}\frac {Q}{P_{\mathrm {n}}}&=&\frac {{\dot E}_{\mathrm {r}}}{E_{\mathrm {n}}}\frac {\overline {\dot I}}{I_{\mathrm {n}}} \\[ 5pt ]
P+\mathrm {j}Q &=&{\dot E}_{\mathrm {r}} \overline {\dot I} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となります。単位法で表す場合,\( \ 3 \ \)倍する必要がないことに注意して下さい。
同様に,受電端電圧(線間電圧)を\( \ {\dot V}_{\mathrm {r}} \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm {r}} \ \mathrm {[p.u.]}&=&\frac {V_{\mathrm {r}} \ \mathrm {[V]}}{V_{\mathrm {n}}}=\frac {\sqrt {3}E_{\mathrm {r}} \ \mathrm {[V]}}{\sqrt {3}E_{\mathrm {n}}}=\frac {E_{\mathrm {r}} \ \mathrm {[V]}}{E_{\mathrm {n}}}=E_{\mathrm {r}} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,
\[
\begin{eqnarray}
P+\mathrm {j}Q &=&{\dot V}_{\mathrm {r}} \overline {\dot I} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
で求めることができます。
【解答】
(1)連系点の電圧\( \ V_{r} \ \mathrm {[p.u.]} \ \)の\( \ R \ \),\( \ X \ \),\( \ P \ \),\( \ Q \ \)からなる簡易な式
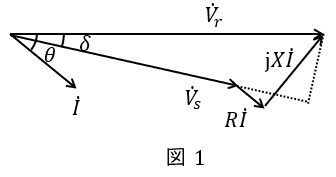
\( \ {\dot V}_{r} \ \)を基準としたベクトル図を図1に示す。ただし,\( \ \delta \ \)は相差角,\( \ \theta \ \)は力率角とする。
図1において,\( \ \delta \ \)が十分に小さいとすれば,
\[
\begin{eqnarray}
V_{r} &≃&V_{s}+RI\cos \left( \theta -\delta \right) +XI\sin \left( \theta -\delta \right) \\[ 5pt ]
&≃&V_{s}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ P=V_{r}I\cos \theta \ \)及び\( \ Q=V_{r}I\sin \theta \ \)より,
\[
\begin{eqnarray}
V_{r} &=&V_{s}+R\cdot \frac {P}{V_{r}}+X\cdot \frac {Q}{V_{r}} \\[ 5pt ]
V_{r}^{2} &=&V_{s}V_{r}+RP+XQ \\[ 5pt ]
V_{r}^{2}- V_{s}V_{r}-\left( RP+XQ\right) &=&0 \\[ 5pt ]
V_{r}&=&\frac {V_{s}±\sqrt {V_{s}^{2}+4\left( RP+XQ\right) }}{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ V_{s}=1.0 \ \mathrm {[p.u.]} \ \)を代入すると,
\[
\begin{eqnarray}
V_{r}&=&\frac {1.0±\sqrt {1.0+4\left( RP+XQ\right) }}{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,与えられている近似式\( \ \sqrt {1+4\left( RP+XQ\right) } ≒ 1+2\left( RP+XQ\right) \ \)より,
\[
\begin{eqnarray}
V_{r}&≒&\frac {1.0±\left\{ 1.0+2\left( RP+XQ\right) \right\} }{2} \\[ 5pt ]
&≒&1.0+RP+XQ,-RP-XQ \left( 不適\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)風力発電所の力率を\( \ 100 \ \mathrm {[%]} \ \)一定で運転した場合,連系点の電圧変動率\( \ \mathrm {[%]} \ \)
風力発電所の最大出力\( \ P \ \mathrm {[p.u.]} \ \)は,基準電力が\( \ 100 \ \mathrm {[MV\cdot A]} \ \)であるから,
\[
\begin{eqnarray}
P&=&\frac {60 000\times 10^{3}}{100\times 10^{6}} \\[ 5pt ]
&=&0.6 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,本設問においては力率\( \ 1 \ \)であるため\( \ Q=0 \ \mathrm {[p.u.]} \ \)となるから,(1)解答式より受電端電圧\( \ V_{r} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
V_{r}&=&1.0+RP+\left( X_{t}+X_{L}\right) Q \\[ 5pt ]
&=&1.0+0.15\times 0.6+\left( 0.1+0.2\right) \times 0 \\[ 5pt ]
&=&1.09 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,風力発電所が無負荷時の連系点電圧が\( \ V_{s}=1.0 \ \mathrm {[p.u.]} \ \)であることから,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{r}-V_{s}}{V_{s}}\times 100 \\[ 5pt ]
&=&\frac {1.09-1.0}{1.0}\times 100 \\[ 5pt ]
&=&9.0 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)連系点での電圧変動率を\( \ 2.0 \ \mathrm {[%]} \ \)とするための連系点での風力発電所の運転力率\( \ \mathrm {[%]} \ \)
電圧変動率が\( \ \varepsilon ^{\prime }=2 \ \mathrm {[%]} \ \)なので,受電端電圧\( \ V_{r}^{\prime } \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\varepsilon ^{\prime }&=&\frac {V_{r}^{\prime }-V_{s}}{V_{s}}\times 100 \\[ 5pt ]
V_{r}^{\prime }-V_{s}&=&\frac {\varepsilon ^{\prime }V_{s}}{100} \\[ 5pt ]
V_{r}^{\prime }&=&V_{s}+\frac {\varepsilon ^{\prime }V_{s}}{100} \\[ 5pt ]
&=&1.0+\frac {2\times 1}{100} \\[ 5pt ]
&=&1.02 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)解答式に各値を代入して,最大出力時の無効電力\( \ Q \ \mathrm {[p.u.]} \ \)を求めると,
\[
\begin{eqnarray}
V_{r}^{\prime }&=&1.0+RP+\left( X_{t}+X_{L}\right) Q \\[ 5pt ]
\left( X_{t}+X_{L}\right) Q&=&V_{r}^{\prime }-1.0-RP \\[ 5pt ]
Q&=&\frac {V_{r}^{\prime }-1.0-RP}{X_{t}+X_{L}} \\[ 5pt ]
&=&\frac {1.02-1.0-0.15\times 0.6}{0.1+0.2} \\[ 5pt ]
&≒&-0.23333 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,このときの力率\( \ \cos \theta \ \)は,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{\sqrt {P^{2}+Q^{2}}} \\[ 5pt ]
&=&\frac {0.6}{\sqrt {0.6^{2}+\left( -0.23333\right) ^{2}}} \\[ 5pt ]
&≒&0.932 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 93.2 \ \mathrm {%} \ \)(進み)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん