【問題】
【難易度】★★★☆☆(普通)
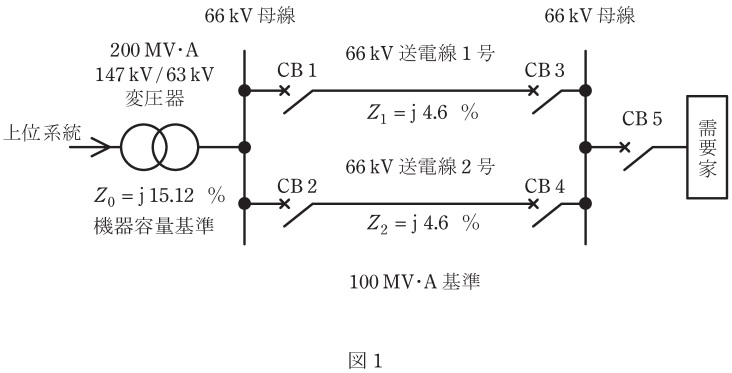
図1のように,電気事業者の変電所から\( \ 66 \ \mathrm {kV} \ \)架空送電線\( \ 2 \ \)回線を併用して受電する特別高圧需要家がある。送電線には,回線ごとに再閉路システムが備えられているとする。需要家に至るまでの送変電系統は,理想的であるとして,変圧器上位系統の背後インピーダンス及び抵抗損失を無視するものとする。次の問に答えよ。ただし,\( \ Z_{0} \ \)は変圧器の漏れインピーダンス,\( \ Z_{1} \ \)及び\( \ Z_{2} \ \)は各送電線の正相インピーダンスである。
(1) 電力系統に発生する事故によって,需要家は,瞬時電圧低下を経験する可能性がある。瞬時電圧低下とは,どのような現象であるのかを説明せよ。
(2) 需要家の負荷は定インピーダンス特性とし,負荷容量は,受電電圧が\( \ 60 \ \mathrm {kV} \ \)のときに\( \ 48000 \ \mathrm {kV\cdot A} \ \)であるとする。力率が遅れ\( \ 0.8 \ \)のとき,負荷の正相インピーダンスの抵抗分とリアクタンス分は,それぞれ何オームか。
(3) 需要家は,送電線\( \ 2 \ \)回線を併用して受電しているとする。変電所の上位系統電圧が\( \ 154 \ \mathrm {kV} \ \)で,負荷の正相インピーダンスが\( \ 80+\mathrm {j}60 \ \mathrm {\Omega } \ \)であるとき,需要家の受電電圧の大きさは,何ボルトになるか。
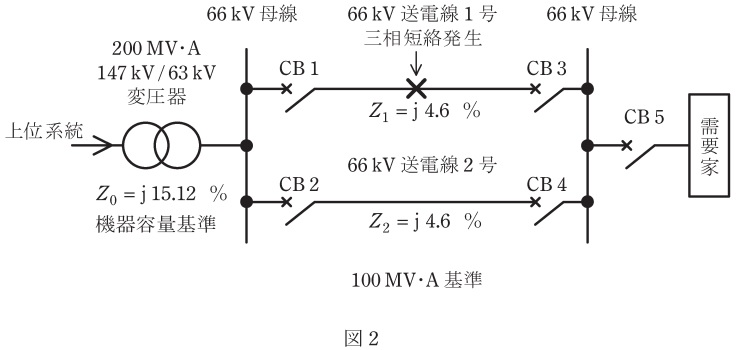
(4) (3)の状態で受電しているときに,\( \ 1 \ \)号線のちょうど中間の地点で,三相短絡事故が発生した(図2)。この事故が除去されるまでの間,需要家の受電電圧の大きさは,何ボルトになるか。
【ワンポイント解説】
この問題は実際に解いてみれば分かりますが,(4)を解くのに時間がかかり,30分ではとても終わらない問題です。過去問に類題もあるため対策をしていれば解けそうな問題ですが,こういう時は例え解けると思っても見切りをつけて他の問題を解き,時間が余れば解くという選択をした方が良いと思います。
1.%インピーダンス
インピーダンスの大きさが\( \ Z \ \mathrm {[\Omega ]} \ \),線路の定格線間電圧が\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),定格電流が\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)である時,%インピーダンスの大きさ\( \ %Z \ \)は,
\[
\begin{eqnarray}
%Z&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}} \times 100 \\[ 5pt ]
\end{eqnarray}
\]
で定義され,三相容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)とすると,
\[
\begin{eqnarray}
%Z&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \times 100 \\[ 5pt ]
&=&\frac {ZP_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \times 100 \\[ 5pt ]
\end{eqnarray}
\]
となります。
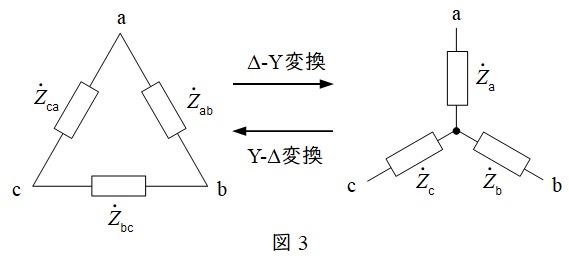
2.\(\mathrm {\Delta – Y}\)変換と\(\mathrm {Y – \Delta}\)変換
毎年のように理論科目で出題されていると思います。一種では不平衡負荷を扱うため,確実に暗記しておく必要があります。
a.\(\mathrm {\Delta – Y}\)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}} &=& \frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}} &=& \frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}}
\end{eqnarray}
\]
b.\(\mathrm {Y – \Delta}\)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}}
\end{eqnarray}
\]
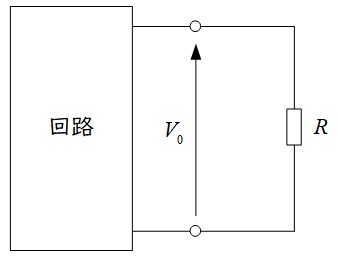
3.テブナンの定理
下図において回路中の2端子の開放電圧を\( \ V_{0} \ \),電圧源を短絡し,電流源を開放した時の端子から見た合成抵抗を\( \ R_{0} \ \)とした時,外部抵抗\( \ R \ \)とした時,抵抗\( \ R \ \)を流れる電流\( \ I \ \)は,下式の通りとなります。
\[
\begin{eqnarray}
I&=&\frac {V_{0}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
※リアクトルでも同様に計算することが可能です。
【関連する「電気の神髄」記事】
【解答】
(1)瞬時電圧低下とは,どのような現象であるか
(ポイント)
・解答の通りですが,影響の出る時間や影響の出る機器についてもう少し具体的に書いても良いかもしれません。
・瞬時電圧低下は落雷等の一線地絡事故が生じた際に,保護リレーが動作し,当該送電線の遮断器を開放して事故除去するまでの約\( \ 100 \ \mathrm {ms} \ \)程度の時間発生する電圧降下で,事故点に近いほど電圧降下が大きくなります。
・瞬時電圧低下の影響のある機器は,コンピュータ(\( \ \mathrm {UPS} \ \)のない場合),サイリスタ式可変速電動機,高圧放電ランプ,リレー(整定時間が短い場合)等があります。
(試験センター解答例)
瞬時電圧低下とは,落雷などにより電力系統に事故が発生すると,事故点を中心に電圧が低下して事故点を電力系統から切り離すまでの短い時間,電圧低下が継続することをいう。需要家にとっては,系統電圧が突然低下した後に短時間で復帰する現象で,コンピュータシステムや自動化が進んだ生産設備の停止等,様々な障害のきっかけとなる。
(2)負荷の正相インピーダンスの抵抗分とリアクタンス分は,それぞれ何オームか
負荷容量を\( \ S_{\mathrm {r}}=P_{\mathrm {r}}+\mathrm {j}Q_{\mathrm {r}} \ \),負荷のインピーダンスを\( \ Z_{\mathrm {r}}=R_{\mathrm {r}}+\mathrm {j}X_{\mathrm {r}} \ \)とする。また,受電電圧を\( \ V_{\mathrm {r}}=60 \ \mathrm {kV} \ \)と置く。
題意の条件の時の電流値を\( \ I \ \)とすると,
\[
\begin{eqnarray}
S_{\mathrm {r}}&=&\sqrt {3}V_{\mathrm {r}}I \\[ 5pt ]
V_{\mathrm {r}}&=&\sqrt {3}Z_{\mathrm {r}}I \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,
\[
\begin{eqnarray}
Z_{\mathrm {r}}&=&\frac {V_{\mathrm {r}}}{\sqrt {3}I} \\[ 5pt ]
&=&\frac {V_{\mathrm {r}}^{2}}{\sqrt {3}V_{\mathrm {r}}I} \\[ 5pt ]
&=&\frac {V_{\mathrm {r}}^{2}}{S_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
と整理でき,各値を代入すると,
\[
\begin{eqnarray}
Z_{\mathrm {r}}&=&\frac {\left( 60\times 10^{3}\right) ^{2}}{48000\times 10^{3}} \\[ 5pt ]
&=&75 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。力率\( \ \cos \theta =0.8 \ \)であるので,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8 ^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,抵抗分とリアクタンス分の大きさは,
\[
\begin{eqnarray}
R_{\mathrm {r}} &=&Z_{\mathrm {r}}\cos \theta \\[ 5pt ]
&=&75\times 0.8 \\[ 5pt ]
&=&60 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {r}} &=&Z_{\mathrm {r}}\sin \theta \\[ 5pt ]
&=&75\times 0.6 \\[ 5pt ]
&=&45 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)変電所の上位系統電圧が\( \ 154 \ \mathrm {kV} \ \)で,負荷の正相インピーダンスが\( \ 80+\mathrm {j}60 \ \mathrm {\Omega } \ \)であるとき,需要家の受電電圧の大きさ
変電所の低圧側の電圧の大きさ\( \ V_{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {n}} &=&\frac {63}{147}\times 154 \\[ 5pt ]
&=&66 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
である。ワンポイント解説「1.%インピーダンス」より,\( \ Z_{0} \ \),\( \ Z_{1} \ \),\( \ Z_{2} \ \)をオーム値に換算すると,
\[
\begin{eqnarray}
Z_{0} \ \mathrm {[\Omega ]} &=&\frac {%Z_{0}V_{\mathrm {n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\mathrm {j}15.12 \times \left( 63\times 10^{3}\right) ^{2}}{100\times 200\times 10^{6}} \\[ 5pt ]
&≒&\mathrm {j}3.0006 \ \mathrm {[\Omega ]} \\[ 5pt ]
Z_{1} \ \mathrm {[\Omega ]} &=&\frac {%Z_{1}V_{\mathrm {n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\mathrm {j}4.6 \times \left( 66\times 10^{3}\right) ^{2}}{100\times 100\times 10^{6}} \\[ 5pt ]
&≒&\mathrm {j}2.0038 \ \mathrm {[\Omega ]} \\[ 5pt ]
Z_{2} \ \mathrm {[\Omega ]} &=&\frac {%Z_{2}V_{\mathrm {n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\mathrm {j}4.6 \times \left( 66\times 10^{3}\right) ^{2}}{100\times 100\times 10^{6}} \\[ 5pt ]
&≒&\mathrm {j}2.0038 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,系統の回路は図1-1のように書くことができる。
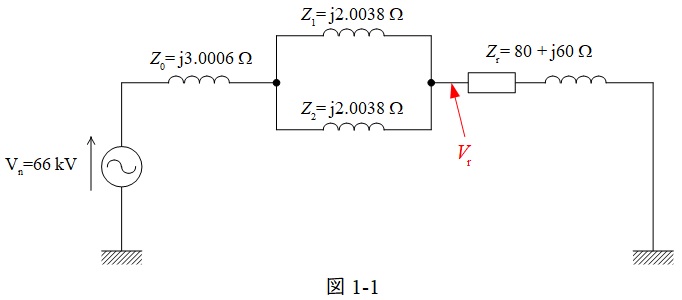
図1-1より受電電圧の大きさ\( \ V_{\mathrm {r}} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{\mathrm {r}} &=&\frac {Z_{\mathrm {r}}}{\displaystyle Z_{0}+\frac {Z_{1}Z_{2}}{Z_{1}+Z_{2}}+Z_{\mathrm {r}}} V_{\mathrm {n}} \\[ 5pt ]
&=&\left| \frac {80+\mathrm {j}60}{\displaystyle \mathrm {j}3.0006+\frac {\mathrm {j}2.0038\times \mathrm {j}2.0038}{\mathrm {j}2.0038+\mathrm {j}2.0038}+80+\mathrm {j}60}\right| \times 66 \\[ 5pt ]
&=&\left| \frac {80+\mathrm {j}60}{\displaystyle \mathrm {j}3.0006+\mathrm {j}1.0019+80+\mathrm {j}60}\right| \times 66 \\[ 5pt ]
&=&\left| \frac {80+\mathrm {j}60}{80+\mathrm {j}64.0025}\right| \times 66 \\[ 5pt ]
&≒&\frac {100}{102.45} \times 66 \\[ 5pt ]
&≒&64.422 → 64.4 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)三相短絡事故が発生し除去されるまでの間,需要家の受電電圧の大きさ
\( \ 1 \ \)号線のちょうど中間の地点で,三相短絡事故が発生した時の等価回路は(3)と同様に図2-1のように描ける。
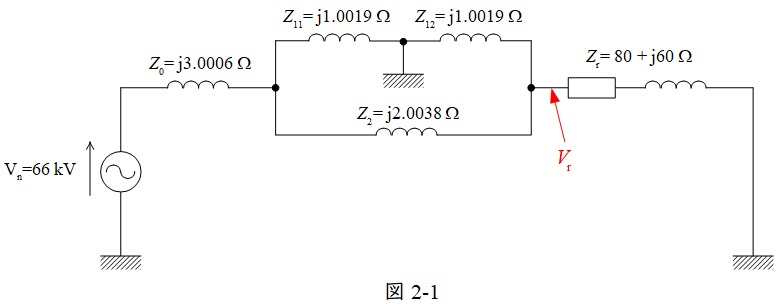
図2-1において,中央部の\( \ \Delta \ \)結線を\(\mathrm {\Delta – Y}\)変換し,それぞれのインピーダンスを\( \ Z_{\mathrm {A}} \ \),\( \ Z_{\mathrm {B}} \ \),\( \ Z_{\mathrm {C}} \ \)とすると,ワンポイント解説「2.\(\mathrm {\Delta – Y}\)変換と\(\mathrm {Y – \Delta}\)変換」より,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {A}} &=& \frac {{\dot Z}_{\mathrm {11}}{\dot Z}_{\mathrm {2}}}{{\dot Z}_{\mathrm {11}}+{\dot Z}_{\mathrm {12}}+{\dot Z}_{\mathrm {2}}} \\[ 5pt ]
&=& \frac {\mathrm {j}1.0019\times \mathrm {j}2.0038}{\mathrm {j}1.0019+\mathrm {j}1.0019+\mathrm {j}2.0038} \\[ 5pt ]
&=& \mathrm {j}0.50095 \mathrm {[\Omega ]} \\[ 5pt ]
{\dot Z}_{\mathrm {B}} &=& \frac {{\dot Z}_{\mathrm {2}}{\dot Z}_{\mathrm {12}}}{{\dot Z}_{\mathrm {11}}+{\dot Z}_{\mathrm {12}}+{\dot Z}_{\mathrm {2}}} \\[ 5pt ]
&=& \frac {\mathrm {j}2.0038\times \mathrm {j}1.0019}{\mathrm {j}1.0019+\mathrm {j}1.0019+\mathrm {j}2.0038} \\[ 5pt ]
&=& \mathrm {j}0.50095 \mathrm {[\Omega ]} \\[ 5pt ]
{\dot Z}_{\mathrm {C}} &=& \frac {{\dot Z}_{\mathrm {12}}{\dot Z}_{\mathrm {11}}}{{\dot Z}_{\mathrm {11}}+{\dot Z}_{\mathrm {12}}+{\dot Z}_{\mathrm {2}}} \\[ 5pt ]
&=& \frac {\mathrm {j}1.0019\times \mathrm {j}1.0019}{\mathrm {j}1.0019+\mathrm {j}1.0019+\mathrm {j}2.0038} \\[ 5pt ]
&≒& \mathrm {j}0.25048 \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,図2-2のように書き換えられる。
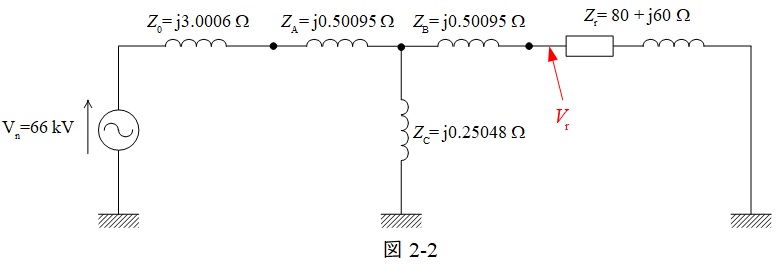
図2-2の受電端電圧\( \ V_{\mathrm {r}} \ \)の箇所において,テブナンの定理を適用すると,受電端開放電圧\( \ V_{0} \ \)は,
\[
\begin{eqnarray}
V_{0} &=& \frac {{\dot Z}_{\mathrm {C}}}{{\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {A}}+{\dot Z}_{\mathrm {C}}}V_{\mathrm {n}} \\[ 5pt ]
&=& \frac {\mathrm {j}0.25048}{\mathrm {j}3.0006+\mathrm {j}0.50095+\mathrm {j}0.25048}\times 66 \\[ 5pt ]
&≒& 4.4061 \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
となり,受電端側から見た合成インピーダンス\( \ {\dot Z}^{\prime } \ \)は,
\[
\begin{eqnarray}
{\dot Z}^{\prime } &=& {\dot Z}_{\mathrm {B}}+\frac {\left( {\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {A}}\right) {\dot Z}_{\mathrm {C}}}{\left( {\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {A}}\right) +{\dot Z}_{\mathrm {C}}} \\[ 5pt ]
&=& \mathrm {j}0.50095+\frac {\left( \mathrm {j}3.0006+\mathrm {j}0.50095\right) \times \mathrm {j}0.25048}{\left( \mathrm {j}3.0006+\mathrm {j}0.50095\right) +\mathrm {j}0.25048} \\[ 5pt ]
&≒& \mathrm {j}0.73471 \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図2-3のように書き換えられる。
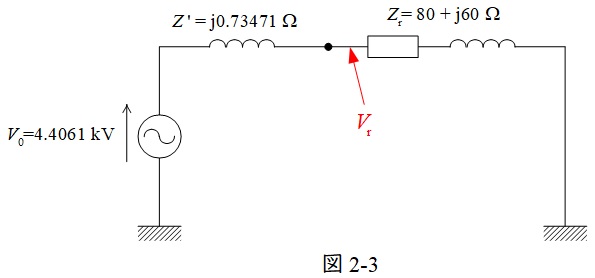
図2-3より,受電端電圧の大きさ\( \ V_{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {r}} &=& \left| \frac {{\dot Z}_{\mathrm {r}}}{{\dot Z}^{\prime }+{\dot Z}_{\mathrm {r}}}\right| V_{0} \\[ 5pt ]
&=& \left| \frac {80+\mathrm {j}60}{\mathrm {j}0.73471+80+\mathrm {j}60}\right| \times 4.4061 \\[ 5pt ]
&≒& \frac {100}{100.44}\times 4.4061 \\[ 5pt ]
&≒& 4.3868 → 4.39 \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん