【問題】
【難易度】★★☆☆☆(やや易しい)
図に示した変電所において効率的な運転を行いたい。\( \ 3 \ \)台の変圧器は同一特性である。変圧器\( \ 1 \ \)台当たりの定格容量を\( \ P_{\mathrm {n}} \ \),鉄損を\( \ P_{\mathrm {i}} \ \),銅損を\( \ P_{\mathrm {c}} \ \),変圧器の負荷側の電圧を\( \ V \ \),電流を\( \ I \ \),力率を\( \ 1 \ \)としたとき,変圧器\( \ 1 \ \)台当たりの効率\( \ \eta \ \)は①式で表される。なお,変圧器は全て定格電圧で運転されており,鉄損\( \ P_{\mathrm {i}} \ \)は\( \ V \ \),\( \ I \ \)に依存せず,銅損\( \ P_{\mathrm {c}} \ \)は電流\( \ I^{2} \ \)に比例する。また,遮断器\( \ \left( \mathrm {CB}\right) \ \)の開閉の前後で母線電圧は変化しないものとする。
\[
\begin{eqnarray}
\eta &=&\frac {\sqrt{3}VI}{\sqrt{3}VI+P_{\mathrm {i}}+P_{\mathrm {c}}}\times 100 \ \mathrm {[%]} ・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
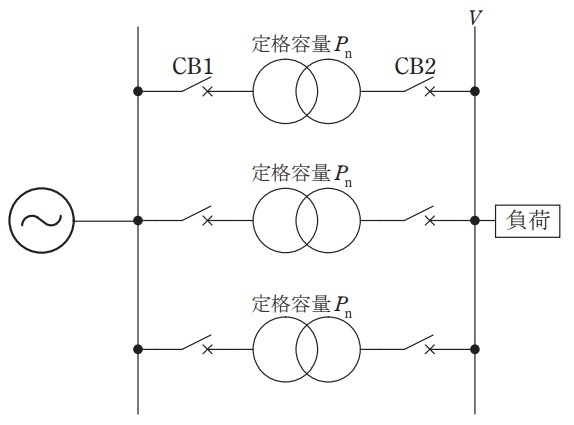
変圧器\( \ 3 \ \)台運転から,\( \ \mathrm {CB1}\cdot \mathrm {CB2} \ \)を開いて変圧器\( \ 2 \ \)台運転とした方が,変電所の効率が高くなる全変圧器負荷容量\( \ L \ \)の範囲を次のa)~f)に従い求めよ。ただし,変圧器\( \ 1 \ \)台当たりの定格運転時の銅損を\( \ P_{\mathrm {c0}} \ \)とする。
a) 全変圧器負荷容量が\( \ L \ \)のときの変圧器\( \ n \ \)台運転時の\( \ 1 \ \)台当たりの銅損\( \ P_{\mathrm {c1}} \ \)を\( \ L \ \),\( \ P_{\mathrm {c0}} \ \),\( \ P_{\mathrm {n}} \ \),\( \ n \ \)を用いて表せ。
b) \( \ n \ \)台運転時の変圧器の全損失\( \ W_{\mathrm {n}} \ \)を\( \ L \ \),\( \ P_{\mathrm {i}} \ \),\( \ P_{\mathrm {c0}} \ \),\( \ P_{\mathrm {n}} \ \),\( \ n \ \)を用いて表せ。
c) \( \ \left( n-1\right) \ \)台で運転したときの変圧器の全損失\( \ W_{\mathrm {n-1}} \ \)を\( \ L \ \),\( \ P_{\mathrm {i}} \ \),\( \ P_{\mathrm {c0}} \ \),\( \ P_{\mathrm {n}} \ \),\( \ n \ \)を用いて表せ。ただし,\( \ n≧2 \ \)とする。
d) \( \ W_{\mathrm {n-1}}<W_{\mathrm {n}} \ \)の関係式を用いて\( \ W_{\mathrm {2}}<W_{\mathrm {3}} \ \)となる全変圧器負荷容量\( \ L \ \)の範囲を\( \ P_{\mathrm {i}} \ \),\( \ P_{\mathrm {c0}} \ \),\( \ P_{\mathrm {n}} \ \)を用いて表せ。
次に,変圧器は負荷率\( \ \varepsilon \ \)のときに最高効率\( \ k\left( <1\right) \ \)をとるものとし,このとき②式が成り立つ。
鉄損\( \ P_{\mathrm {i}} \ = \ \)銅損\( \ P_{\mathrm {c}} ・・・・・・・・・・・・・・・・・・・・・・ ② \ \)
e) 変圧器\( \ 1 \ \)台当たりの\( \ P_{\mathrm {i}} \ \)と\( \ P_{\mathrm {c0}} \ \)を\( \ P_{\mathrm {n}} \ \),\( \ k \ \),\( \ \varepsilon \ \)を用いて表せ。
f) 前問d)における\( \ W_{\mathrm {2}}<W_{\mathrm {3}} \ \)となる全変圧器負荷容量\( \ L \ \)の範囲を\( \ \varepsilon \ \),\( \ P_{\mathrm {n}} \ \)を用いて表せ。
【ワンポイント解説】
変圧器の効率的な運用に関する問題です。
条件がすべて与えられ,その場で考えながら解いていくいかにも\( \ 1 \ \)種らしい問題と言えます。
合格に向けては本問のような問題を確実に選択し,高得点できるようになることが重要です。
【解答】
a)全変圧器負荷容量が\( \ L \ \)のときの変圧器\( \ n \ \)台運転時の\( \ 1 \ \)台当たりの銅損\( \ P_{\mathrm {c1}} \ \)
変圧器\( \ 1 \ \)台あたりの負荷分担は\( \ \displaystyle \frac {L}{n} \ \)であり,銅損は負荷の\( \ 2 \ \)乗に比例するから,
\[
\begin{eqnarray}
P_{\mathrm {c1}}&=&\left( \frac {\displaystyle \frac {L}{n}}{P_{\mathrm {n}}}\right) ^{2}P_{\mathrm {c0}} \\[ 5pt ]
&=&\frac {L^{2}P_{\mathrm {c0}}}{{P_{\mathrm {n}}}^{2}n^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
b)\( \ n \ \)台運転時の変圧器の全損失\( \ W_{\mathrm {n}} \ \)
\( \ 1 \ \)台あたりの全損失\( \ W_{\mathrm {1}} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {1}}&=&P_{\mathrm {i}}+P_{\mathrm {c1}} \\[ 5pt ]
&=&P_{\mathrm {i}}+\frac {L^{2}P_{\mathrm {c0}}}{{P_{\mathrm {n}}}^{2}n^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ n \ \)台運転時の変圧器の全損失\( \ W_{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {n}}&=&nW_{\mathrm {1}} \\[ 5pt ]
&=&n\left( P_{\mathrm {i}}+\frac {L^{2}P_{\mathrm {c0}}}{{P_{\mathrm {n}}}^{2}n^{2}}\right) \\[ 5pt ]
&=&nP_{\mathrm {i}}+\frac {L^{2}P_{\mathrm {c0}}}{{P_{\mathrm {n}}}^{2}n} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
c)\( \ \left( n-1\right) \ \)台で運転したときの変圧器の全損失\( \ W_{\mathrm {n-1}} \ \)
b)の解答式を\( \ n→\left( n-1\right) \ \)に置き換えると,
\[
\begin{eqnarray}
W_{\mathrm {n-1}}&=&\left( n-1\right) P_{\mathrm {i}}+\frac {L^{2}P_{\mathrm {c0}}}{{P_{\mathrm {n}}}^{2}\left( n-1\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
d)\( \ W_{\mathrm {2}}<W_{\mathrm {3}} \ \)となる全変圧器負荷容量\( \ L \ \)の範囲
b),c)の解答式に\( \ n=3 \ \)を代入して\( \ W_{\mathrm {2}}<W_{\mathrm {3}} \ \)の式を整理すると,
\[
\begin{eqnarray}
W_{\mathrm {2}}&<&W_{\mathrm {3}} \\[ 5pt ]
2 P_{\mathrm {i}}+\frac {L^{2}P_{\mathrm {c0}}}{{P_{\mathrm {n}}}^{2}\times 2 }&<&3 P_{\mathrm {i}}+\frac {L^{2}P_{\mathrm {c0}}}{{P_{\mathrm {n}}}^{2}\times 3 } \\[ 5pt ]
\frac {L^{2}P_{\mathrm {c0}}}{2{P_{\mathrm {n}}}^{2} }-\frac {L^{2}P_{\mathrm {c0}}}{3{P_{\mathrm {n}}}^{2} }&<& P_{\mathrm {i}} \\[ 5pt ]
\frac {L^{2}P_{\mathrm {c0}}}{6{P_{\mathrm {n}}}^{2} }&<& P_{\mathrm {i}} \\[ 5pt ]
L^{2}&<& \frac {6{P_{\mathrm {n}}}^{2} P_{\mathrm {i}}}{P_{\mathrm {c0}}} \\[ 5pt ]
L&<& P_{\mathrm {n}}\sqrt {\frac {6 P_{\mathrm {i}}}{P_{\mathrm {c0}}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
e)変圧器\( \ 1 \ \)台当たりの\( \ P_{\mathrm {i}} \ \)と\( \ P_{\mathrm {c0}} \ \)
①式より導出される負荷率\( \ \varepsilon \ \)のときの効率\( \ \eta \left( =k\times 100\right) \ \)から\( \ k \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {\varepsilon P_{\mathrm {n}}}{\varepsilon P_{\mathrm {n}}+P_{\mathrm {i}}+\varepsilon ^{2}P_{\mathrm {c0}}}\times 100 \\[ 5pt ]
k &=&\frac {\varepsilon P_{\mathrm {n}}}{\varepsilon P_{\mathrm {n}}+P_{\mathrm {i}}+\varepsilon ^{2}P_{\mathrm {c0}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より\( \ P_{\mathrm {i}}=\varepsilon ^{2}P_{\mathrm {c0}} \ \)であるから,
\[
\begin{eqnarray}
k &=&\frac {\varepsilon P_{\mathrm {n}}}{\varepsilon P_{\mathrm {n}}+2P_{\mathrm {i}}} \\[ 5pt ]
\varepsilon P_{\mathrm {n}}+2P_{\mathrm {i}} &=&\frac {\varepsilon P_{\mathrm {n}}}{k} \\[ 5pt ]
2P_{\mathrm {i}} &=&\frac {\varepsilon P_{\mathrm {n}}}{k}-\varepsilon P_{\mathrm {n}} \\[ 5pt ]
&=&\varepsilon P_{\mathrm {n}}\frac {1-k}{k} \\[ 5pt ]
P_{\mathrm {i}}&=&\varepsilon P_{\mathrm {n}}\frac {1-k}{2k} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ P_{\mathrm {c0}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {c0}} &=&\frac {P_{\mathrm {i}}}{\varepsilon ^{2}} \\[ 5pt ]
&=&\varepsilon P_{\mathrm {n}}\frac {1-k}{2k}\cdot \frac {1}{\varepsilon ^{2}} \\[ 5pt ]
&=& P_{\mathrm {n}}\frac {1-k}{2\varepsilon k} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
f)\( \ W_{\mathrm {2}}<W_{\mathrm {3}} \ \)となる全変圧器負荷容量\( \ L \ \)の範囲
d)解答式にe)解答式を代入すると,
\[
\begin{eqnarray}
L&<& P_{\mathrm {n}}\sqrt {\frac {6 P_{\mathrm {i}}}{P_{\mathrm {c0}}}} \\[ 5pt ]
&=& P_{\mathrm {n}}\sqrt {\frac {6 \displaystyle \varepsilon P_{\mathrm {n}}\frac {1-k}{2k}}{\displaystyle P_{\mathrm {n}}\frac {1-k}{2\varepsilon k}}} \\[ 5pt ]
&=& P_{\mathrm {n}}\sqrt {\frac {6 \displaystyle \varepsilon }{\displaystyle \frac {1}{\varepsilon }}} \\[ 5pt ]
&=& P_{\mathrm {n}}\sqrt {6\varepsilon ^{2}} \\[ 5pt ]
&=& \sqrt {6}P_{\mathrm {n}}\varepsilon \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん