【問題】
【難易度】★★☆☆☆(やや易しい)
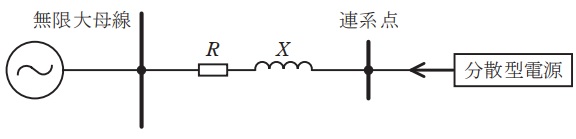
図のように,抵抗\( \ R \ \)とリアクタンス\( \ X \ \)とをもつ電線路を介して分散型電源が無限大母線と連系して運転している。無限大母線の電圧の大きさを\( \ V_{\mathrm {S}} \ \mathrm {[kV]} \ \),分散型電源の連系点電圧の大きさを\( \ V \ \mathrm {[kV]} \ \)とする。分散型電源の出力が大きくなると,連系点が過電圧となる可能性があるため,保安確保の面から電圧管理が必要となる。\( \ V_{\mathrm {S}} \ \mathrm {[kV]} \ \)を基準電圧,\( \ 10 \ \mathrm {MV\cdot A} \ \)を基準容量としたとき,抵抗\( \ R \ \)の値が\( \ r \ \mathrm {[p.u.]} \ \),リアクタンス\( \ X \ \)の値が\( \ x \ \mathrm {[p.u.]} \ \)であった。次の問に答えよ。ただし,無限大母線電圧\( \ V_{\mathrm {S}} \ \mathrm {[kV]} \ \)は,分散型電源の出力によらず,一定とする。
(1) 分散型電源が連系される前の連系点での短絡容量を\( \ \mathrm {p.u.} \ \)の単位で求めよ。
(2) 連系点電圧\( \ V \ \mathrm {[kV]} \ \)の単位法表示を\( \ v \ \mathrm {[p.u.]} \ \)とする。無限大母線電圧に対する連系点電圧の位相差を無視できるならば,分散型電源の有効出力が\( \ p \ \mathrm {[p.u.]} \ \),無効出力(発電機の遅れ側を正とする。)が\( \ q \ \mathrm {[p.u.]} \ \)のとき,連系点電圧\( \ v \ \mathrm {[p.u.]} \ \)が次式で求められることを示せ。
\[
\begin{eqnarray}
v &=&1+r\cdot p+x\cdot q \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
ただし,\( \ r \ \)と\( \ q \ \)は小さいので,\( \ 1 \ \)に比べて小さな\( \ a \ \)に関する次の近似式を用いてもよい。
\[
\begin{eqnarray}
\sqrt {1+a} &≈&1+0.5a \\[ 5pt ]
\end{eqnarray}
\]
(3) 連系点電圧の上限値が\( \ 1.06 \ \mathrm {p.u.} \ \)であるとする。\( \ r \ \)が\( \ 0.05 \ \mathrm {p.u.} \ \),\( \ x \ \)が\( \ 0.1 \ \mathrm {p.u.} \ \)であるとき,力率\( \ 1 \ \),有効電力\( \ 14 \ \mathrm {MW} \ \)で運転する分散型電源が連系できるか否かを計算過程及び判断根拠とともに述べよ。
(4) 小問(3)において分散型電源の無効電力が\( \ -2.0 \ \mathrm {Mvar} \ \)のとき,連系できる最大有効電力\( \ \mathrm {[MW]} \ \)を求めよ。
【ワンポイント解説】
分散型電源の系統連系に関する問題です。
(2)の変形に少し頭を悩ませますが,過去にも類題等が出題されているので,問題なく解けた受験生も多かったと思います。本問は合格のためにはぜひ選択しておきたい問題と言えるでしょう。
1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時,インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.単位法における容量換算
「1.オーム法から単位法への変換」の通り,単位法のインピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \mathrm {[V\cdot A]} \ \)から\( \ P_{\mathrm {B}} \ \mathrm {[V\cdot A]} \ \)へ変換する場合の単位法におけるインピーダンスは,
\[
\begin{eqnarray}
Z_{\mathrm {B}} \ \mathrm {[p.u.]}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}Z_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.単位法による短絡電流計算
単位法における短絡インピーダンスを\( \ Z_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)とすると,三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は,基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※単位法の定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが,試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ]
&=&\frac {1}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}}\times I_{\mathrm {n}} \\[ 5pt ]
&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
4.短絡容量と単位法におけるインピーダンスの関係
単位法における短絡インピーダンスを\( \ Z_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)とすると,短絡容量\( \ P_{\mathrm {s}} \ \mathrm {[V\cdot A]} \ \)は,基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)を用いて,
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\frac {P_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※以下の通り,単位法による短絡電流計算の式より求められます。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\sqrt {3}V_{\mathrm {n}}I_{\mathrm {s}}&=&\frac {\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
P_{\mathrm {s}}&=&\frac {P_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)分散型電源が連系される前の連系点での短絡容量\( \ \mathrm {[p.u.]} \ \)
ワンポイント解説「4.短絡容量と単位法におけるインピーダンスの関係」の短絡容量の式より,
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\frac {P_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\frac {P_{\mathrm {s}}}{P_{\mathrm {n}}}&=&\frac {\displaystyle \frac {P_{\mathrm {n}}}{P_{\mathrm {n}}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
P_{\mathrm {s}} \ \mathrm {[p.u.]}&=&\frac {1}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
であり,短絡インピーダンス\( \ Z_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)が,
\[
\begin{eqnarray}
Z_{\mathrm {s}}&=&\sqrt {r^{2}+x^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\frac {1}{\sqrt {r^{2}+x^{2}}} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)連系点電圧\( \ v \ \mathrm {[p.u.]} \ \)が\( \ v =1+r\cdot p+x\cdot q \ \)で求められることを示す
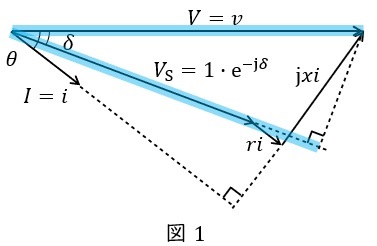
題意に沿ってベクトル図を描くと図1のようになる。ただし,\( \ V \ \)と\( \ I \ \)の位相差を\( \ \theta \ \),\( \ V \ \)と\( \ V_{\mathrm {S}} \ \)の位相差を\( \ \delta \ \)とする。
無限大母線電圧に対する連系点電圧の位相差を無視できるので,図1に太線で示す長さはほぼ等しいと考えられるから,
\[
\begin{eqnarray}
v&≈&1+ri\cos \left( \theta -\delta \right) +xi\sin \left( \theta -\delta \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに\( \delta \ \)が十分に小さいとすれば,
\[
\begin{eqnarray}
v&≈&1+ri\cos \theta +xi\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,
\[
\begin{eqnarray}
p&=&vi\cos \theta \\[ 5pt ]
i\cos \theta &=&\frac {p}{v} \\[ 5pt ]
q&=&vi\sin \theta \\[ 5pt ]
i\sin \theta &=&\frac {q}{v} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
v&≈&1+\frac {rp}{v} +\frac {xq}{v} \\[ 5pt ]
v^{2}&=&v+rp+xq \\[ 5pt ]
v^{2}-v-\left( rp+xq\right) &=&0 \\[ 5pt ]
v &=&\frac {1±\sqrt {1+4\left( rp+xq\right) }}{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ v>0 \ \)より,
\[
\begin{eqnarray}
v &=&\frac {1+\sqrt {1+4\left( rp+xq\right) }}{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,\( \ r \ \)と\( \ q \ \)は小さいので,与えられている\( \ 1 \ \)に比べて小さな値に関する近似式を適用すると,
\[
\begin{eqnarray}
v &≈&\frac {1+\left\{ 1+2\left( rp+xq\right) \right\}}{2} \\[ 5pt ]
&=&1+rp+xq \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)力率\( \ 1 \ \),有効電力\( \ 14 \ \mathrm {MW} \ \)で運転する分散型電源が連系できるか否か
基準容量が\( \ 10 \ \mathrm {MV\cdot A} \ \),力率が\( \ 1 \ \)であるから,分散型電源の有効電力\( \ p=1.4 \ \mathrm {[p.u.]} \ \)で無効電力\( \ q=0 \ \mathrm {[p.u.]} \ \)となる。
(2)解答式にそれぞれ代入すると,
\[
\begin{eqnarray}
v &≈&1+rp+xq \\[ 5pt ]
&=&1+0.05\times 1.4+0.1\times 0 \\[ 5pt ]
&=&1.07 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,連系点電圧が上限値\( \ 1.06 \ \mathrm {p.u.} \ \)を超えるため,分散型電源は連系できない。
(4)分散型電源の無効電力が\( \ -2.0 \ \mathrm {Mvar} \ \)のとき,連系できる最大有効電力\( \ \mathrm {[MW]} \ \)
基準容量が\( \ 10 \ \mathrm {MV\cdot A} \ \)なので,分散型電源の無効電力\( \ q=-0.2 \ \mathrm {[p.u.]} \ \)となる。
(2)解答式に上限値\( \ v=1.06 \ \mathrm {[p.u.]} \ \)及び各値を代入すると,
\[
\begin{eqnarray}
v &≈&1+rp+xq \\[ 5pt ]
1.06&=&1+0.05p+0.1\times \left( -0.2\right) \\[ 5pt ]
0.05p&=&0.08 \\[ 5pt ]
p&=&1.6 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,連系できる最大有効電力は\( \ 16 \ \mathrm {[MW]} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん