【問題】
【難易度】★★★☆☆(普通)
水力発電所の建設計画を策定するにあたって,河川流況は極めて重要である。
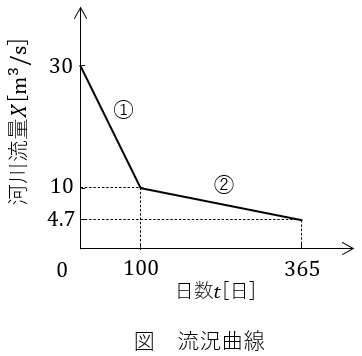
ここに,①,②式の直線近似式で示される図の流況曲線の河川がある。この河川に有効落差\( \ H=40 \ \mathrm {m} \ \)の自流式(流れ込み式)水力発電所を建設したい。
ここで,河川流量\( \ X \ \mathrm {[m^{3}/s]} \ \)は日数\( \ t \ [日] \ \)の関数とし,
\( \ 0≦t<100 \ \)のとき:\( \ X=30-0.2t \ \ ・・・・・・・・・・・ ① \ \)
\( \ \ 100≦t≦365 \ \)のとき:\( \ X=12-0.02t ・・・・・・・・・・・ ② \ \)
で示される。この発電所計画において,発電に用いる最大使用水量\( \ Q_{\mathrm {max}} \ \mathrm {[m^{3}/s]} \ \)は年間平均流量の\( \ 2 \ \)倍とすることとする。
また,水車・発電機の総合効率\( \ \eta \ \mathrm {[%]} \ \)は,使用水量\( \ Q \ \mathrm {[m^{3}/s]} \ \)によって変化するものとし,計算の便宜上,以下によって与えられる。
\( \ \ \ 10≦Q \ \)のとき:\( \ 90 \ % ・・・・・・・・・・・・・・・・・・ ③ \ \)
\( \ 5≦Q<10 \ \)のとき:\( \ 60 \ % ・・・・・・・・・・・・・・・・・・ ④ \ \)
\( \ \ \ \ Q<5 \ \)のとき:\( \ \ 0 \ % \ ・・・・・・・・・・・・・・・・・・ ⑤ \ \)
なお,発電出力\( \ P \ \mathrm {[kW]} \ \)は\( \ P=9.8 QH\eta \ \)で表され,\( \ 1 \ \)年間は\( \ 365 \ \)日とする。
次の問に答えよ。
(1) この発電所の計画最大出力\( \ P_{\mathrm {max}} \ \mathrm {[kW]} \ \)を求めよ。
(2) この計画において,最大使用水量で発電できる期間の累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)を求めよ。
(3) この計画において,最大使用水量未満での累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)を求めよ。
(4) この発電所の計画年間発電電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)及び計画設備利用率\( \ [%] \ \)を求めよ。
(5) 上記の結果を踏まえ計画の変更を検討したいが,どのような観点で計画変更を検討するべきかを\( \ 50 \ \)字程度以内で述べよ。
但し,落差,効率は変更できないものとする。
【ワンポイント解説】
水力発電所の流況曲線の検討に関する問題です。
(1)と(2)は絶対に間違えてはいけない問題,(3)以降で差をつけさせる問題という印象です。
内容自体はそれほど難解ではありませんので,本番でも常に落ち着いて計算間違いに注意して解くようにして下さい。
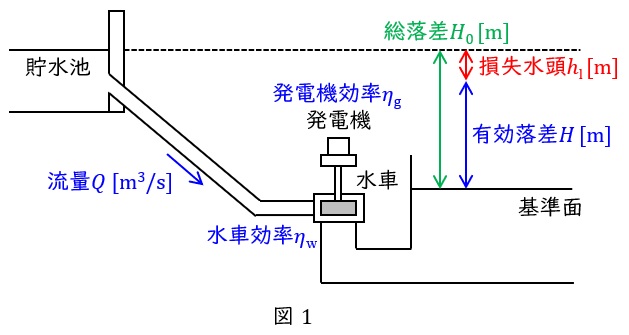
1.水力発電所の出力\( \ P \ \)
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}/s]} \ \),有効落差\( \ H \ \mathrm {[m]} \ \),水車効率\( \ \eta _{\mathrm {w}} \ \),発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると,発電機の出力\( \ P \ \mathrm {[kW]} \ \)は
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。これは重力加速度\( \ g=9.8 \ \mathrm {[m/s^{2}]} \ \)及び水の密度\( \ \rho =1 \ 000 \ \mathrm {[kg/m^{3}]} \ \)を使用した時の発電機の出力である
\[
\begin{eqnarray}
P &=&\rho gQH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
に各値を代入し,
\[
\begin{eqnarray}
P &=&1 \ 000 \times 9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ]
&=&9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
として導出したものです。
2.設備利用率
最大出力で\( \ 1 \ \)年間運転し続けた電力量に対する実際の電力量の割合です。
最大出力\( \ P \ \mathrm {[kW]} \ \),年間発電電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)であるとき,\( \ 1 \ \)日が\( \ 24 \ \)時間,\( \ 1 \ \)年が\( \ 365 \ \)日であるとすると,設備利用率\( \ \alpha \ \)は,
\[
\begin{eqnarray}
\alpha &=&\frac {W}{P\times 24 \times 365} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)発電所の計画最大出力\( \ P_{\mathrm {max}} \ \mathrm {[kW]} \ \)
流況曲線より年間平均流量\( \ Q_{\mathrm {av}} \ \mathrm {[m^{3}/s]} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {av}}&=&\frac {\displaystyle \frac {30+10}{2}\times 100+\frac {10+4.7}{2}\times 265}{365} \\[ 5pt ]
&≒&10.816 \ \mathrm {[m^{3}/s]} \\[ 5pt ]
\end{eqnarray}
\]
なので,最大使用水量\( \ Q_{\mathrm {max}} \ \mathrm {[m^{3}/s]} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {max}}&=&2Q_{\mathrm {av}} \\[ 5pt ]
&=&2\times 10.816 \\[ 5pt ]
&=&21.632 \ \mathrm {[m^{3}/s]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,発電所の計画最大出力\( \ P_{\mathrm {max}} \ \mathrm {[kW]} \ \)は,ワンポイント解説「1.水力発電所の出力\( \ P \ \)」の通り,
\[
\begin{eqnarray}
P_{\mathrm {max}}&=&9.8Q_{\mathrm {max}}H\eta \\[ 5pt ]
&=&9.8\times 21.632\times 40 \times 0.9 \\[ 5pt ]
&≒&7 \ 631.8 → 7 \ 630 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)最大使用水量で発電できる期間の累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)
①式より,最大使用水量\( \ Q_{\mathrm {max}}=21.632 \ \mathrm {[m^{3}/s]} \ \)で運転できる日数\( \ t_{1} \ [日] \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {max}} &=&30-0.2t_{1} \\[ 5pt ]
21.632 &=&30-0.2t_{1} \\[ 5pt ]
0.2t_{1} &=&30-21.632 \\[ 5pt ]
t_{1} &=&41.84 \ [日] \\[ 5pt ]
\end{eqnarray}
\]
なので,最大使用水量で発電できる期間の累計発電電力量\( \ W_{1} \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{1} &=&P_{\mathrm {max}}\times 24\times t_{1} \\[ 5pt ]
&=&7 \ 631.8\times 24\times 41.84 \\[ 5pt ]
&≒&7 \ 663 \ 500 → 7.66\times 10^{6} \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
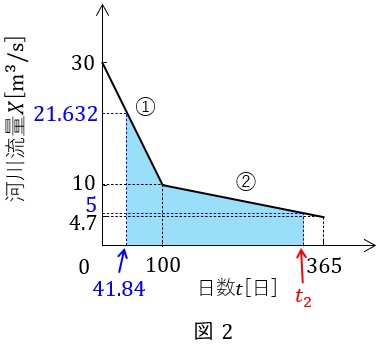
(3)最大使用水量未満での累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)
\( \ Q<5 \ \mathrm {[m^{3}/s]} \ \)のとき効率は\( \ 0 \ % \ \)なので,流況曲線における最大使用水量未満で発電する領域は図2の通りとなる。図2における\( \ t_{2} \ [日] \ \)は,
\[
\begin{eqnarray}
X &=&12-0.02t_{2} \\[ 5pt ]
5 &=&12-0.02t_{2} \\[ 5pt ]
0.02t_{2} &=&7 \\[ 5pt ]
t_{2}&=&350 \ [日] \\[ 5pt ]
\end{eqnarray}
\]
となる。この領域の①式の領域の年間平均流量\( \ Q_{\mathrm {av1}} \ \mathrm {[m^{3}/s]} \ \)及び②の領域の年間平均流量\( \ Q_{\mathrm {av2}} \ \mathrm {[m^{3}/s]} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {av1}}&=&\frac {21.632+10}{2} \\[ 5pt ]
&≒&15.816 \ \mathrm {[m^{3}/s]} \\[ 5pt ]
Q_{\mathrm {av2}}&=&\frac {10+5}{2} \\[ 5pt ]
&=&7.5 \ \mathrm {[m^{3}/s]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,このときの出力\( \ P_{\mathrm {av1}} \ \mathrm {[kW]} \ \)及び\( \ P_{\mathrm {av2}} \ \mathrm {[kW]} \ \)は,ワンポイント解説「1.水力発電所の出力\( \ P \ \)」の通り,
\[
\begin{eqnarray}
P_{\mathrm {av1}}&=&9.8Q_{\mathrm {av1}}H\eta \\[ 5pt ]
&=&9.8\times 15.816\times 40 \times 0.9 \\[ 5pt ]
&≒&5 \ 579.9 \ \mathrm {[kW]} \\[ 5pt ]
P_{\mathrm {av2}}&=&9.8Q_{\mathrm {av2}}H\eta \\[ 5pt ]
&=&9.8\times 7.5\times 40 \times 0.6 \\[ 5pt ]
&=&1 \ 764 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となり,累計発電電力量\( \ W_{2} \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{2}&=&P_{\mathrm {av1}}\times 24 \times \left( 100-41.84\right) +P_{\mathrm {av2}}\times 24 \times \left( 350-100\right) \\[ 5pt ]
&=&5 \ 579.9\times 24 \times \left( 100-41.84\right) +1 \ 764\times 24 \times \left( 350-100\right) \\[ 5pt ]
&≒&18 \ 373 \ 000 → 1.84 \times 10^{7} \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)発電所の計画年間発電電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)及び計画設備利用率\( \ [%] \ \)
(2)及び(3)より,計画年間発電電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W&=&W_{1}+W_{2} \\[ 5pt ]
&=&7 \ 663 \ 500+18 \ 373 \ 000 \\[ 5pt ]
&≒&26 \ 037 \ 000 → 2.60 \times 10^{7} \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,計画設備利用率\( \ \alpha \ [%] \ \)は,ワンポイント解説「2.設備利用率」の通り,
\[
\begin{eqnarray}
\alpha &=&\frac {W}{P_{\mathrm {max}}\times 24 \times 365}\times 100 \\[ 5pt ]
&=&\frac {26 \ 037 \ 000}{7 \ 631.8\times 24 \times 365}\times 100 \\[ 5pt ]
&≒&38.9 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)どのような観点で計画変更を検討するべきか
設備利用率が低いため,\( \ 1 \ \mathrm {kW\cdot h} \ \)当たりの建設コストを最小化するように最大使用水量を見直す必要がある。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん