《電力》〈配電〉[R02:問4]コンクリート柱にかかる荷重と電柱の抵抗モーメントに関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，コンクリート柱に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

配電線の大容量化などに伴う太線化と多回線化による\( \ \fbox {　 （１） 　} \ \)の増加に加え，木材資源が乏しくなってきたことから，現在，我が国では配電系統の支持物（電柱）としてコンクリート柱が主流となっている。電柱には電線をはじめとした種々の設備が取り付けられているため，以下に示す応力について考慮する必要がある。

応力の計算では，電柱の最大応力を生じる部分において，電柱が分担する最悪条件下の外力による\( \ \fbox {　 （２） 　} \ \)モーメント（\( \ M \ \)）より電柱の抵抗モーメント（\( \ M_{\mathrm {r}} \ \)）が大きくなるように設計する必要がある。

外力による\( \ \fbox {　 （２） 　} \ \)モーメント（\( \ M \ \)）は，以下のa)，b)の和で表される。

a)　電柱全体に加わる風圧による\( \ \fbox {　 （２） 　} \ \)モーメント（\( \ M_{\mathrm {p}} \ \)）
\[
\begin{eqnarray}
M_{\mathrm {p}} &=& \ \fbox {　 （３） 　} \ \mathrm {[kg \cdot m ]} \\[ 5pt ] \end{eqnarray}
\] ただし，\( \ w_{\mathrm {p}} \ \)：円形柱体の単位面積当たりの風圧荷重\( \ \mathrm {[kg / m^{2} ]} \ \)，\( \ D_{\mathrm {0}} \ \)：電柱地際における直径\( \ \mathrm {[cm]} \ \)，\( \ H \ \)：電柱の地表上の高さ\( \ \mathrm {[m]} \ \)，\( \ K \ \)：電柱の直径増加係数。

b)　電線に加わる風圧による\( \ \fbox {　 （２） 　} \ \)モーメント（\( \ M_{\mathrm {w}} \ \)）
\[
\begin{eqnarray}
M_{\mathrm {w}} &=& \ \fbox {　 （４） 　} \ \mathrm {[kg \cdot m ]} \\[ 5pt ] \end{eqnarray}
\] ただし，\( \ w_{\mathrm {e}} \ \)：電線の\( \ \fbox {　 （５） 　} \ \)投影面積当たりの風圧荷重\( \ \mathrm {[kg / m^{2} ]} \ \)，\( \ d \ \)：電線の直径\( \ \mathrm {[mm]} \ \)，\( \ h \ \)：電線の地表上の高さ\( \ \mathrm {[m]} \ \)，\( \ S \ \)：径間\( \ \mathrm {[m]} \ \)
したがって，定められた風圧荷重に対して次式を満足させる必要がある。
\[
\begin{eqnarray}
M_{\mathrm {r}} &＞&M=M_{\mathrm {p}}+M_{\mathrm {w}} \\[ 5pt ] \end{eqnarray}
\]

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　水平　　　　　&（ロ）&　曲げ　　　　　&（ハ）&　w_{\mathrm {p}}\left( \frac {{D_{0}}^{2}H^{2}}{200}-\frac {{KH}^{4}}{3}\right) \\[ 5pt ] &（ニ）&　活線作業　　　　　&（ホ）&　設計荷重　　　　　&（ヘ）&　S\frac {\sum w_{\mathrm {e}}dh }{1000} \\[ 5pt ] &（ト）&　ねじれ　　　　　&（チ）&　S^{2}\frac {\sum w_{\mathrm {e}}dh }{1000}　　　　　　&（リ）&　w_{\mathrm {p}}\left( \frac {{D_{0}}H^{2}}{200}-\frac {{KH}^{3}}{3}\right) \\[ 5pt ] &（ヌ）&　S\frac {\sum w_{\mathrm {e}}d^{2}h }{1000}　　　　　&（ル）&　垂直　　　　　&（ヲ）&　直角 \\[ 5pt ] &（ワ）&　圧縮　　　　　&（カ）&　w_{\mathrm {p}}\left( \frac {{D_{0}}H}{200}-\frac {{KH}^{2}}{3}\right)　　　　　&（ヨ）&　引っ張り \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電柱に加わる荷重に関する出題です。
\( \ 2 \ \)種までの電験のテキストでは取扱いのない分野からの出題で，少し受験生を驚かせた問題かもしれません。(1)及び(2)は文脈から何となく類推できるような内容，(5)は基本事項なので，知識がなくてもこのような選択肢を落とさないことが重要となります。

1.電柱に加わる風圧による曲げモーメント\( \ M_{\mathrm {p}} \ \mathrm {[kg \cdot m ]} \ \)
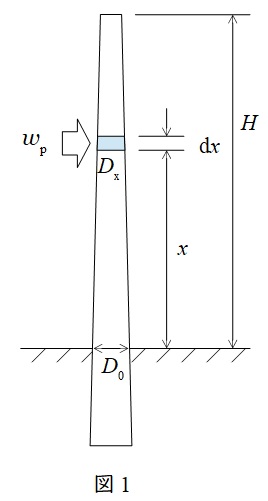
図1のようなモデルの電柱に加わる風圧による曲げモーメント\( \ M_{\mathrm {p}} \ \mathrm {[kg \cdot m ]} \ \)を考えます。
図1において，高さ\( \ x \ \mathrm {[m]} \ \)の地点における直径\( \ D_{\mathrm {x}} \ \mathrm {[cm]} \ \)は，電柱地際における直径を\( \ D_{\mathrm {0}} \ \mathrm {[cm]} \ \)，電柱の直径増加係数を\( \ K \ \)とすると，
\[
\begin{eqnarray}
\frac {D_{\mathrm {x}}}{100} &=&\frac {D_{\mathrm {0}}}{100}-Kx \\[ 5pt ] &=&\frac {D_{\mathrm {0}}-100Kx}{100} \\[ 5pt ] \end{eqnarray}
\] となります。単位面積当たりに加わる風圧荷重を\( \ w_{\mathrm {p}} \ \mathrm {[kg / m^{2} ]} \ \)とすると，高さ\( \ x \ \mathrm {[m]} \ \)の地点の微小区間\( \ \mathrm {d}x \ \mathrm {[m]} \ \)に加わる風圧による曲げモーメント\( \ \mathrm {d}M_{\mathrm {p}} \ \mathrm {[kg \cdot m ]} \ \)は，
\[
\begin{eqnarray}
\mathrm {d}M_{\mathrm {p}} &=&w_{\mathrm {p}}\cdot \frac {D_{\mathrm {x}}}{100}\mathrm {d}x \cdot x \\[ 5pt ] &=&w_{\mathrm {p}}\frac {D_{\mathrm {0}}-100Kx}{100} x\mathrm {d}x \\[ 5pt ] &=&\frac {w_{\mathrm {p}}\left( D_{\mathrm {0}}x-100Kx^{2}\right) }{100} \mathrm {d}x \\[ 5pt ] \end{eqnarray}
\] となるので，電柱全体に加わる曲げモーメント\( \ M_{\mathrm {p}} \ \mathrm {[kg \cdot m ]} \ \)は，両辺を積分すると，
\[
\begin{eqnarray}
M_{\mathrm {p}} &=&\int _{0}^{H}\frac {w_{\mathrm {p}}\left( D_{\mathrm {0}}x-100Kx^{2}\right) }{100} \mathrm {d}x \\[ 5pt ] &=&\frac {w_{\mathrm {p}}}{100}\int _{0}^{H}\left( D_{\mathrm {0}}x-100Kx^{2}\right) \mathrm {d}x \\[ 5pt ] &=&\frac {w_{\mathrm {p}}}{100}\left[ \frac {D_{\mathrm {0}}x^{2}}{2}-\frac {100Kx^{3}}{3}\right] _{0}^{H} \\[ 5pt ] &=&\frac {w_{\mathrm {p}}}{100}\left( \frac {{D_{0}}H^{2}}{2}-\frac {100KH^{3}}{3}\right) \\[ 5pt ] &=&w_{\mathrm {p}}\left( \frac {{D_{0}}H^{2}}{200}-\frac {KH^{3}}{3}\right) \\[ 5pt ] \end{eqnarray}
\] となります。

2.電線に加わる風圧による電柱の曲げモーメント\( \ M_{\mathrm {w}} \ \mathrm {[kg \cdot m ]} \ \)
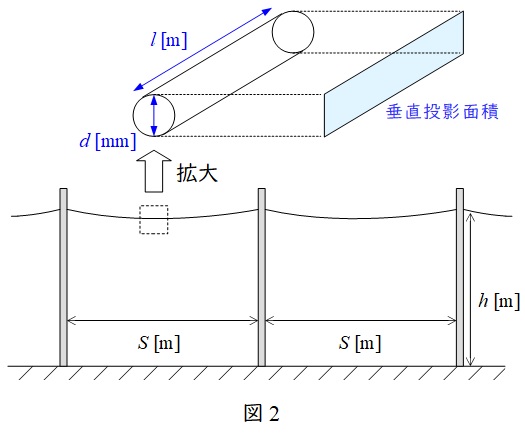
図2のようなモデルの中央の電柱に加わる曲げモーメント\( \ M_{\mathrm {w}} \ \mathrm {[kg \cdot m ]} \ \)を考えます。
中央の電柱が分担する電線の長さは，\( \ \displaystyle \frac {S}{2}+\frac {S}{2}=S \ \)なので，電線に加わる風圧荷重の垂直投影面積\( \ A \ \mathrm {[m^{2}]} \ \)は，電線の直径を\( \ d \ \mathrm {[mm]} \ \)とすると，
\[
\begin{eqnarray}
A &=&\frac {d}{1000}\cdot S \\[ 5pt ] &=&\frac {Sd}{1000} \\[ 5pt ] \end{eqnarray}
\] となります。電線の単位垂直投影面積当たりの風圧荷重を\( \ w_{\mathrm {e}} \ \mathrm {[kg / m^{2} ]} \ \)とすると，高さ\( \ h \ \mathrm {[m]} \ \)の電線による電柱に加わるモーメント\( \ M_{\mathrm {w}} \ \mathrm {[kg \cdot m ]} \ \)は，
\[
\begin{eqnarray}
M_{\mathrm {w}} &=&w_{\mathrm {e}}A\times h \\[ 5pt ] &=&\frac {w_{\mathrm {e}}Sdh}{1000} \\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(1)解答：ホ
題意より解答候補は，（ニ）活線作業，（ホ）設計荷重，（ヨ）引っ張り，等になると思います。
いずれも配電線の大容量化や多回線化により増加する可能性が高いですが，本問に内容に最も合っているのは設計荷重となります。

(2)解答：ロ
題意より解答候補は，（イ）水平，（ロ）曲げ，（ト）ねじれ，（ル）垂直，（ワ）圧縮，（ヨ）引っ張り，等になると思います。
ワンポイント解説「1.電柱に加わる風圧による曲げモーメント\( \ M_{\mathrm {p}} \ \mathrm {[kg \cdot m ]} \ \)」や「2.電線に加わる風圧による電柱の曲げモーメント\( \ M_{\mathrm {w}} \ \mathrm {[kg \cdot m ]} \ \)」でも検討しているように，問題文の内容に最も合致しているのは曲げモーメントとなります。

(3)解答：リ
題意より解答候補は，（ハ）\( \ \displaystyle w_{\mathrm {p}}\left( \frac {{D_{0}}^{2}H^{2}}{200}-\frac {{KH}^{4}}{3}\right) \ \)，（リ）\( \ \displaystyle w_{\mathrm {p}}\left( \frac {{D_{0}}H^{2}}{200}-\frac {{KH}^{3}}{3}\right) \ \)，（カ）\( \ \displaystyle w_{\mathrm {p}}\left( \frac {{D_{0}}H}{200}-\frac {{KH}^{2}}{3}\right) \ \)，になると思います。
ワンポイント解説「1.電柱に加わる風圧による曲げモーメント\( \ M_{\mathrm {p}} \ \mathrm {[kg \cdot m ]} \ \)」の通り，電柱に加わる風圧による曲げモーメントとして適切なのは，\( \ \displaystyle w_{\mathrm {p}}\left( \frac {{D_{0}}H^{2}}{200}-\frac {{KH}^{3}}{3}\right) \ \)となります。

(4)解答：ヘ
題意より解答候補は，（ヘ）\( \ \displaystyle S\frac {\sum w_{\mathrm {e}}dh }{1000} \ \)，（チ）\( \ \displaystyle S^{2}\frac {\sum w_{\mathrm {e}}dh }{1000} \ \)，（ヌ）\( \ \displaystyle S\frac {\sum w_{\mathrm {e}}d^{2}h }{1000} \ \)，になると思います。
ワンポイント解説「2.電線に加わる風圧による電柱の曲げモーメント\( \ M_{\mathrm {w}} \ \mathrm {[kg \cdot m ]} \ \)」の通り，電線\( \ 1 \ \)線あたりの電柱に加わるモーメント\( \ M_{\mathrm {w}} \ \mathrm {[kg \cdot m ]} \ \)は，
\[
\begin{eqnarray}
M_{\mathrm {w}} &=&\frac {w_{\mathrm {e}}Sdh}{1000} \\[ 5pt ] \end{eqnarray}
\] となるので，複数の電線になる場合，
\[
\begin{eqnarray}
M_{\mathrm {w}} &=&S\frac {\sum w_{\mathrm {e}}dh }{1000} \\[ 5pt ] \end{eqnarray}
\] と求められます。

(5)解答：ル
題意より解答候補は，（イ）水平，（ル）垂直，（ヲ）直角，等になると思います。
ワンポイント解説「2.電線に加わる風圧による電柱の曲げモーメント\( \ M_{\mathrm {w}} \ \mathrm {[kg \cdot m ]} \ \)」の通り，電線を横から見た時に投影される面積を垂直投影面積と言います。電気設備技術基準の解釈に出てくる用語になります。