【問題】
【難易度】★★☆☆☆(やや易しい)
水力発電所と二つの火力発電所\( \ \mathrm {G_{1}} \ \),\( \ \mathrm {G_{2}} \ \)からなる電源から供給している系統がある。水力発電所を昼間・夜間一定運転した場合の,火力発電所の需要分担は下表のとおりであり,火力発電所の出力\( \ P \ \mathrm {[MW]} \ \)に対する増分燃料費\( \ \lambda \ \)は,下式のとおりとする。

火力発電所\( \ \mathrm {G_{1}} \ \):\( \ \lambda _{1}\left( P_{1}\right)=1 \ 000+12P_{1} \ \)
火力発電所\( \ \mathrm {G_{2}} \ \):\( \ \lambda _{2}\left( P_{2}\right)=650+20P_{2} \ \)
これから,水力発電所を夜間時間帯に停止し,停止中に調整池に貯留した分の水を昼間時間帯に出力増加して使い切ることで,火力発電所の出力を平準化するものとして,次の\( \ \fbox { (1) } \ \)から\( \ \fbox { (5) } \ \)に当てはまる数値を求め,記述用紙の解答欄に記入しなさい(答の有効数字は\( \ 3 \ \)けたとする。)。
なお,調整池への河川流入量\( \ \mathrm {[m^{3} / s]} \ \)は常に一定で,水力発電所の出力と使用流量\( \ \mathrm {[m^{3} / s]} \ \)とは比例関係にあるものとする。また,系統の送電損失は無視するものとする。
水力発電所による調整前,火力発電所\( \ \mathrm {G_{1}} \ \),\( \ \mathrm {G_{2}} \ \)の\( \ \lambda \ \)特性から経済的に出力配分すると,\( \ \mathrm {G_{1}} \ \)の発電出力は昼間時間帯が\( \ \fbox { (1) } \ \mathrm {[MW]} \ \),夜間時間帯が\( \ \fbox { (2) } \ \mathrm {[MW]} \ \)となる。
水力発電所で夜間時間帯に停止した分に相当する電力量と同じ分の電力量を,昼間時間帯に均等に水力発電所の出力増に充てるものとすると,水力発電所の昼間時間帯の発電出力は\( \ \fbox { (3) } \ \mathrm {[MW]} \ \)になる。
水力発電所による調整後,火力発電所\( \ \mathrm {G_{1}} \ \),\( \ \mathrm {G_{2}} \ \)を経済的に出力配分すると,\( \ \mathrm {G_{1}} \ \)の発電出力は昼間時間帯が\( \ \fbox { (4) } \ \mathrm {[MW]} \ \),夜間時間帯が\( \ \fbox { (5) } \ \mathrm {[MW]} \ \)となる。
【ワンポイント解説】
火力発電所の増分燃料費を用いた計算問題です。
増分燃料費の考え方を理解していれば,かなり高得点を狙うことが可能です。計算間違いや勘違いに十分注意しながら完答を目指すようにして下さい。
1.増分燃料費の考え方
火力発電所は定格容量や使用する燃料の種類等により,出力に対する燃料費の増加の仕方が異なります。
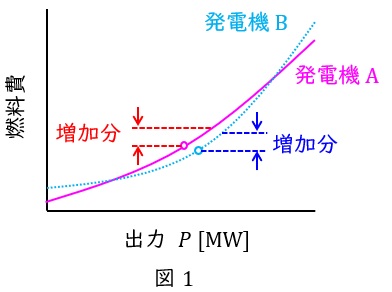
例えば図1に示すような燃料増分費の特性を持つ発電機\( \ \mathrm {A} \ \)と発電機\( \ \mathrm {B} \ \)があった場合,全体として出力を増加させる際にはそれぞれの発電機の燃料費増加分が一緒となるように各発電機の運転出力を調整すると,最も経済的な運転ができるようになります。
【解答】
(1)解答:\( \ 145 \ \)
表より,発電出力の合計が\( \ 250 \ \mathrm {[MW]} \ \)であるから,
\[
\begin{eqnarray}
P_{1}+P_{2} &=&250 ・・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「1.増分燃料費の考え方」の通り,増分燃料費が等しいとき最も経済的な運転が可能なので,
\[
\begin{eqnarray}
1 \ 000+12P_{1} &=&650+20P_{2} \\[ 5pt ]
12P_{1}-20P_{2} &=&-350 \\[ 5pt ]
6P_{1}-10P_{2} &=&-175 ・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ ①\times 10 +② \ \)より,
\[
\begin{eqnarray}
16P_{1} &=&2 \ 325 \\[ 5pt ]
P_{1} &≒&145.31 → 145 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:\( \ 20.3 \ \)
(1)と同様に考えると,
\[
\begin{eqnarray}
P_{1}+P_{2} &=&50 &・・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
6P_{1}-10P_{2} &=&-175 &・・・・・・・・・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ③\times 10 +④ \ \)より,
\[
\begin{eqnarray}
16P_{1} &=&325 \\[ 5pt ]
P_{1} &≒&20.313 → 20.3 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:\( \ 25.7 \ \)
表より,昼間時間帯が\( \ 8 \ \)時から\( \ 22 \ \)時までの\( \ 14 \ \)時間,夜間時間帯が\( \ 22 \ \)時から\( \ 8 \ \)時までの\( \ 10 \ \)時間なので,出力増したときの昼間時間帯の出力\( \ P_{w} \ \mathrm {[MW]} \ \)は,
\[
\begin{eqnarray}
14P_{w} &=&24\times 15 \\[ 5pt ]
P_{w} &≒&25.714 → 25.7 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:\( \ 139 \ \)
水力発電所調整後の火力発電所の昼間時間帯の出力を\( \ P_{d} \ \mathrm {[MW]} \ \),夜間時間帯の出力を\( \ P_{n} \ \mathrm {[MW]} \ \)とすると,
\[
\begin{eqnarray}
P_{d} &=&250-\left( P_{w}-15 \right) \\[ 5pt ]
&=&250-\left( 25.714-15 \right) \\[ 5pt ]
&≒&239.29 \ \mathrm {[MW]} \\[ 5pt ]
P_{n} &=&50+15 \\[ 5pt ]
&=&65 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)と同様に考えると,昼間時間帯においては
\[
\begin{eqnarray}
P_{1}+P_{2} &=&239.29 &・・・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
6P_{1}-10P_{2} &=&-175 &・・・・・・・・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ⑤\times 10 +⑥ \ \)より,
\[
\begin{eqnarray}
16P_{1} &=&2 \ 217.9 \\[ 5pt ]
P_{1} &≒&138.62 → 139 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:\( \ 29.7 \ \)
(4)と同様に,
\[
\begin{eqnarray}
P_{1}+P_{2} &=&65 &・・・・・・・・・・・・・・・・・・ ⑦& \\[ 5pt ]
6P_{1}-10P_{2} &=&-175 &・・・・・・・・・・・・・・・・・・ ⑧& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ⑦\times 10 +⑧ \ \)より,
\[
\begin{eqnarray}
16P_{1} &=&475 \\[ 5pt ]
P_{1} &≒&29.688 → 29.7 \ \mathrm {[MW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん