《機械》〈回転機〉[H22:問2]同期発電機の飽和曲線と短絡曲線に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，同期発電機の飽和曲線と短絡曲線に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句，式又は数値を解答群の中から選びなさい。

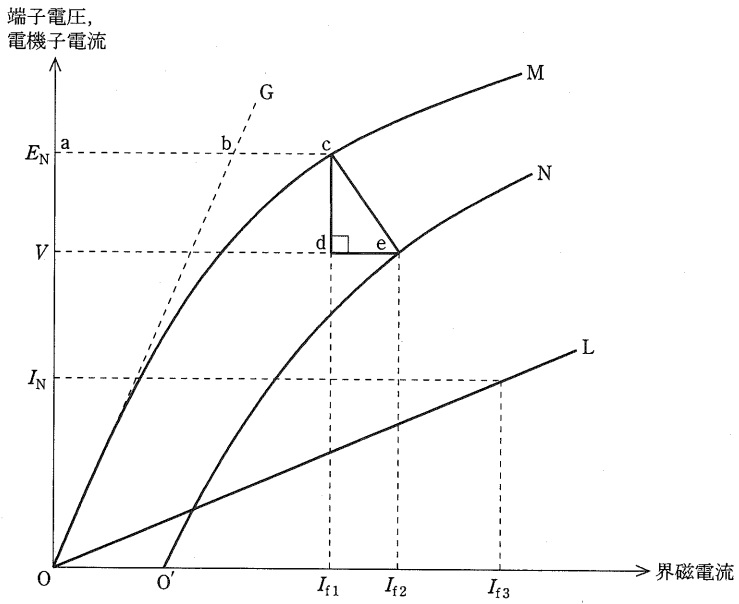
図中の曲線$ \ \mathrm {OM} \ $は，同期発電機が定格速度で無負荷運転しているときの無負荷飽和曲線を示す。また，曲線$ \ \mathrm {O^{\prime }N} \ $は，同じ同期発電機が定格速度で零力率（遅相）負荷運転しているときの負荷飽和曲線を示す。

無負荷飽和曲線において，$ \ E_{\mathrm {N}} \ $を定格電圧，そのときの界磁電流を$ \ I_{\mathrm {f1}} \ $とする。原点を通り無負荷飽和曲線に接する接線$ \ \mathrm {OG} \ $を引き，これが定格電圧$ \ E_{\mathrm {N}} \ $に対応する点を$ \ \mathrm {b} \ $とする。線分$ \ \overline {\mathrm {ab}} \ $は$ \ \fbox {　（１）　} \ $に磁束を通すのに必要な界磁電流に相当し，また，線分$ \ \overline {\mathrm {bc}} \ $は鉄心中に磁束を通すのに必要な界磁電流に相当する。飽和の程度を表す線分の長さの比$ \ \fbox {　（２）　} \ $を飽和率という。

負荷飽和曲線$ \ \mathrm {O^{\prime }N} \ $上の点$ \ \mathrm {e} \ $は，ある負荷をとったときの電圧が$ \ V \ $，界磁電流が$ \ I_{\mathrm {f2}} \ $での運転点である。点$ \ \mathrm {c} \ $から電圧$ \ V \ $に対応する水平線まで垂線を下した点を$ \ \mathrm {d} \ $とすると，線分$ \ \overline {\mathrm {cd}} \ $は$ \ \fbox {　（３）　} \ $による電圧降下に等しく，線分$ \ \overline {\mathrm {de}} \ $は電機子反作用として働く起磁力に相当する界磁電流である。

図中の$ \ \mathrm {OL} \ $は，同期発電機の端子を三相短絡して定格速度で運転したときの短絡曲線を示す。定格電流$ \ I_{\mathrm {N}} \ $を持続して流したときの界磁電流を$ \ I_{\mathrm {f3}} \ $とする。界磁電流$ \ I_{\mathrm {f3}} \ $は，三相短絡時に定格電流による同期インピーダンス降下に等しい電圧を誘起するのに必要な界磁電流と見なせる。また，界磁電流の比$ \ \fbox {　（４）　} \ $を短絡比という。

短絡比の値は，タービン発電機では$ \ \fbox {　（５）　} \ $程度のものが多い。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {I_{\mathrm {f3}}}{I_{\mathrm {f1}}}　　　　　&（ロ）&　磁　極　　　　　&（ハ）&　0.8～1.1 \\[ 5pt ] &（ニ）&　ポーシェリアクタンス　　　　　　　&（ホ）&　\frac {I_{\mathrm {f2}}}{I_{\mathrm {f3}}}　　　　　&（ヘ）&　\frac {\overline {\mathrm {bc}}}{\overline {\mathrm {ab}}} \\[ 5pt ] &（ト）&　0.4～0.6　　　　　&（チ）&　界磁漏れリアクタンス　　　　　　　&（リ）&　1.6～2.5 \\[ 5pt ] &（ヌ）&　ギャップ　　　　　&（ル）&　\frac {\overline {\mathrm {bc}}}{\overline {\mathrm {ac}}}　　　　　　&（ヲ）&　同期リアクタンス \\[ 5pt ] &（ワ）&　\frac {\overline {\mathrm {ab}}}{\overline {\mathrm {ac}}}　　　　　&（カ）&　\frac {I_{\mathrm {f1}}}{I_{\mathrm {f3}}}　　　　　&（ヨ）&　絶縁物 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

同期発電機の飽和曲線と三相短絡曲線に関する問題です。
$ \ 3 \ $種や$ \ 2 \ $種では短絡比を求めるために無負荷飽和曲線と三相短絡曲線を扱いましたが，$ \ 1 \ $種ではもう一歩突っ込んだ内容が出題されますので，本問で覚えるようにして下さい。

1.同期発電機の飽和曲線と短絡曲線
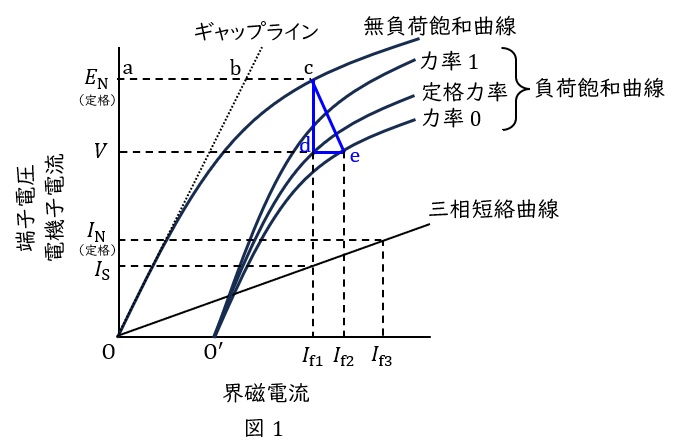
同期発電機の無負荷飽和曲線，負荷飽和曲線，三相短絡曲線を図1に示します。
無負荷飽和曲線は無負荷時の端子電圧と界磁電流の関係を示した曲線で，界磁電流が大きくなると鉄心の磁気飽和により，少しずつ水平に近づいていきます。仮に磁気飽和が無かった場合の直線をギャップラインといいます。
負荷飽和曲線は定格回転速度で，一定電流の負荷をかけたときの端子電圧と界磁電流の関係を示した曲線で，力率により変化します。
三相短絡曲線は発電機の端子を短絡したときの，電機子電流と界磁電流の関係を示した曲線で，通常は直線を描きます。

無負荷飽和曲線において，線分$ \ \overline {\mathrm {ab}} \ $はギャップに磁束を通すのに必要な界磁電流で，また，線分$ \ \overline {\mathrm {bc}} \ $は鉄心中に磁束を通すのに必要な界磁電流で，$ \ \displaystyle \frac {\overline {\mathrm {bc}}}{\overline {\mathrm {ab}}} \ $を飽和率といいます。

負荷飽和曲線において，ある負荷をとったときの電圧$ \ V \ $，界磁電流$ \ I_{\mathrm {f2}} \ $の運転点を点$ \ \mathrm {e} \ $とします。点$ \ \mathrm {c} \ $から電圧$ \ V \ $に対応する水平線まで垂線を下した点を$ \ \mathrm {d} \ $とすると，線分$ \ \overline {\mathrm {cd}} \ $は漏れリアクタンス（ポーシェリアクタンス）による電圧降下に等しく，線分$ \ \overline {\mathrm {de}} \ $は電機子反作用として働く起磁力に相当する界磁電流となります。

無負荷飽和曲線において，定格電圧$ \ E_{\mathrm {N}} \ $を発生させるのに必要な界磁電流を$ \ I_{\mathrm {f1}} \ $，三相短絡曲線において，定格電流$ \ I_{\mathrm {N}} \ $を流すのに必要な界磁電流を$ \ I_{\mathrm {f3}} \ $としたとき，$ \ \displaystyle K=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f3}}}=\frac {I_{\mathrm {S}}}{I_{\mathrm {N}}} \ $を短絡比といいます。

【解答】

(1)解答：ヌ
題意より解答候補は，（ロ）磁極，（ヌ）ギャップ，（ヨ）絶縁物，になると思います。
ワンポイント解説「1.同期発電機の飽和曲線と短絡曲線」の通り，線分$ \ \overline {\mathrm {ab}} \ $はギャップに磁束を通すのに必要な界磁電流となります。

(2)解答：ヘ
題意より解答候補は，（ヘ）$ \ \displaystyle \frac {\overline {\mathrm {bc}}}{\overline {\mathrm {ab}}} \ $，（ル）$ \ \displaystyle \frac {\overline {\mathrm {bc}}}{\overline {\mathrm {ac}}} \ $，（ワ）$ \ \displaystyle \frac {\overline {\mathrm {ab}}}{\overline {\mathrm {ac}}} \ $，になると思います。
ワンポイント解説「1.同期発電機の飽和曲線と短絡曲線」の通り，飽和率は$ \ \displaystyle \frac {\overline {\mathrm {bc}}}{\overline {\mathrm {ab}}} \ $で求められます。

(3)解答：ニ
題意より解答候補は，（ニ）ポーシェリアクタンス，（チ）界磁漏れリアクタンス，（ヲ）同期リアクタンス，になると思います。
ワンポイント解説「1.同期発電機の飽和曲線と短絡曲線」の通り，線分$ \ \overline {\mathrm {cd}} \ $はポーシェリアクタンスによる電圧降下となります。

(4)解答：カ
題意より解答候補は，（イ）$ \ \displaystyle \frac {I_{\mathrm {f3}}}{I_{\mathrm {f1}}} \ $，（ホ）$ \ \displaystyle \frac {I_{\mathrm {f2}}}{I_{\mathrm {f3}}} \ $，（カ）$ \ \displaystyle \frac {I_{\mathrm {f1}}}{I_{\mathrm {f3}}} \ $，になると思います。
ワンポイント解説「1.同期発電機の飽和曲線と短絡曲線」の通り，短絡比は$ \ \displaystyle \frac {I_{\mathrm {f1}}}{I_{\mathrm {f3}}} \ $で求められます。

(5)解答：ト
題意より解答候補は，（ハ）$ \ 0.8～1.1 \ $，（ト）$ \ 0.4～0.6 \ $，（リ）$ \ 1.6～2.5 \ $，になると思います。
タービン発電機の短絡比は$ \ 0.4～0.6 \ $程度のものが多く，水車発電機の$ \ 0.8～1.1 \ $程度に比べ小さいです。