【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,単巻変圧器に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
図1に示すように一次側と二次側とが絶縁されていなくて,巻線の一部が一次と二次に共通に利用されている変圧器を単巻変圧器という。共通部分を分路巻線,残りの部分を\( \ \fbox { (1) } \ \)という。
高圧側電圧を\( \ V_{\mathrm {h}} \ \),低圧側電圧を\( \ V_{\mathrm {l}} \ \),\( \ \fbox { (1) } \ \)及び分路巻線の電圧をそれぞれ,\( \ V_{\mathrm {m}} \ \),\( \ V_{\mathrm {n}} \ \)とし,巻線の漏れインピーダンス及び励磁電流を無視すれば,次の関係がある。
\[
\begin{eqnarray}
V_{\mathrm {h}} &=& V_{\mathrm {m}}+V_{\mathrm {n}} , V_{\mathrm {l}}=V_{\mathrm {n}} & ・・・・・・・・・・・ ①& \\[ 5pt ]
S_{\mathrm {S}} &=& V_{\mathrm {m}}I_{\mathrm {h}}=\left( V_{\mathrm {h}}-V_{\mathrm {l}}\right) I_{\mathrm {h}} & ・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
単巻変圧器では\( \ S_{\mathrm {S}} \ \)を\( \ \fbox { (2) } \ \)といい,負荷に供給できる電力\( \ S_{\mathrm {L}}=V_{\mathrm {h}}I_{\mathrm {h}}=V_{\mathrm {l}}I_{\mathrm {l}} \ \)を負荷容量又は線路容量という。\( \ S_{\mathrm {S}} \ \)は\( \ \fbox { (1) } \ \)と分路巻線を分離して二巻線変圧器として用いた場合の容量で,単巻変圧器の大きさは\( \ S_{\mathrm {S}} \ \)で決まる。\( \ \displaystyle \frac {S_{\mathrm {S}}}{S_{\mathrm {L}}} \ \)を\( \ K \ \)とすると,
\[
\begin{eqnarray}
K &=& 1-\frac {V_{\mathrm {l}}}{V_{\mathrm {h}}} & ・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となり,原理上,\( \ V_{\mathrm {h}} \ \)に対する\( \ V_{\mathrm {l}} \ \)の比が\( \ \fbox { (3) } \ \)に近いほど同一\( \ \fbox { (2) } \ \)に対して線路容量が大きくなる。
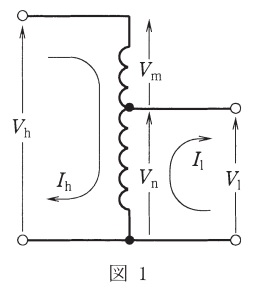
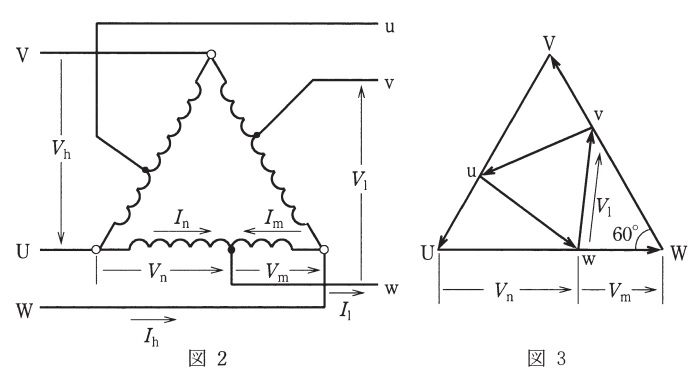
図2は単巻変圧器\( \ 3 \ \)台を用いた三相\( \ \Delta \ \)結線である。図3の電圧ベクトル図から各電圧の関係は次式となる。
\[
\begin{eqnarray}
V_{\mathrm {l}}^{2} &=& \ \fbox { (4) } & ・・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
次に,図2に示す電流\( \ I_{\mathrm {h}} \ \),\( \ I_{\mathrm {l}} \ \),\( \ I_{\mathrm {m}} \ \),\( \ I_{\mathrm {n}} \ \)及び電圧\( \ V_{\mathrm {h}} \ \),\( \ V_{\mathrm {l}} \ \),\( \ V_{\mathrm {m}} \ \),\( \ V_{\mathrm {n}} \ \)を考える。\( \ V_{\mathrm {m}}I_{\mathrm {m}}=V_{\mathrm {n}}I_{\mathrm {n}} \ \)であるから
\[
\begin{eqnarray}
\frac {I_{\mathrm {m}}}{V_{\mathrm {n}}} &=& \frac {I_{\mathrm {n}}}{V_{\mathrm {m}}} = \frac {I_{\mathrm {m}}+I_{\mathrm {n}}}{V_{\mathrm {m}}+V_{\mathrm {n}}}=\frac {I_{\mathrm {l}}}{V_{\mathrm {h}}}& ・・・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ S_{\mathrm {S}} \ \)は⑤式から
\[
\begin{eqnarray}
S_{\mathrm {S}} &=& 3V_{\mathrm {m}}I_{\mathrm {m}}=3\frac {V_{\mathrm {m}}V_{\mathrm {n}}I_{\mathrm {l}}}{V_{\mathrm {h}}} & ・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
である。④,⑥式から\( \ V_{\mathrm {h}} \ \),\( \ V_{\mathrm {l}} \ \)を用いて\( \ \displaystyle K=\frac {S_{\mathrm {S}}}{S_{\mathrm {L}}} \ \)は
\[
\begin{eqnarray}
K &=& \ \fbox { (5) } & ・・・・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& V_{\mathrm {h}}^{2}-3V_{\mathrm {m}}V_{\mathrm {n}} &(ロ)& 分布容量 &(ハ)& 安定巻線 \\[ 5pt ]
&(ニ)& \frac {V_{\mathrm {h}}^{2}-V_{\mathrm {l}}^{2}}{V_{\mathrm {h}}V_{\mathrm {l}}} &(ホ)& \frac {V_{\mathrm {h}}^{2}-V_{\mathrm {l}}^{2}}{\sqrt {3}V_{\mathrm {h}}V_{\mathrm {l}}} &(ヘ)& 自己容量 \\[ 5pt ]
&(ト)& 1 &(チ)& 短絡容量 &(リ)& \sqrt {3} \\[ 5pt ]
&(ヌ)& 直列巻線 &(ル)& \frac {V_{\mathrm {h}}^{2}-V_{\mathrm {l}}^{2}}{3V_{\mathrm {h}}V_{\mathrm {l}}} &(ヲ)& V_{\mathrm {h}}^{2}-V_{\mathrm {m}}V_{\mathrm {n}} \\[ 5pt ]
&(ワ)& V_{\mathrm {h}}^{2}-\sqrt {3}V_{\mathrm {m}}V_{\mathrm {n}} &(カ)& 並列巻線 &(ヨ)& \sqrt {2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
単巻変圧器に関する問題ですが,(1)~(3)までは単巻変圧器の基本的な内容を理解しているかどうか,(4),(5)は数値計算となり,前半と後半で全く違う問題となっています。受験生のレベルや配点を考えると悪くても3つ以上は得点しておきたい問題です。
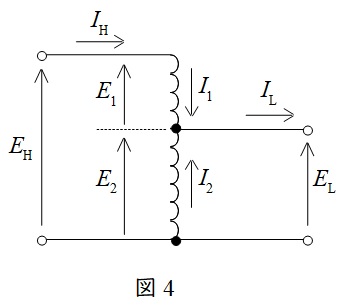
1.単相単巻変圧器
高圧側と低圧側の巻線の一部を共用する変圧器です。共用しない巻線を直列巻線(図4の\( \ E_{1} \ \)に当たる巻線),共用する巻線を分路巻線(図4の\( \ E_{2} \ \)に当たる巻線)と言います。それぞれの電圧を図4のように定義し,自己容量を\( \ P_{1} \ \),分路容量を\( \ P_{2} \ \),線路容量を\( \ P_{3} \ \)とすると,
\[
\begin{eqnarray}
P_{1} &=&E_{1}I_{1} \\[ 5pt ]
&=&\left( E_{\mathrm {H}}-E_{\mathrm {L}}\right) I_{\mathrm {H}} \\[ 5pt ]
P_{2} &=&E_{2}I_{2} \\[ 5pt ]
P_{3} &=&E_{\mathrm {H}}I_{\mathrm {H}} \\[ 5pt ]
&=&E_{\mathrm {L}}I_{\mathrm {L}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
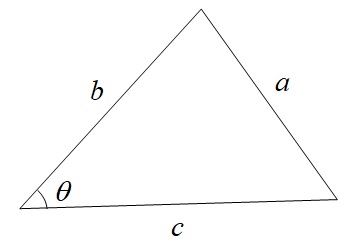
2.余弦定理
下図のような三角形において,
\[
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立します。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ヌ
題意より,解答候補は(ハ)安定巻線,(ヌ)直列巻線,(カ)並列巻線,となると思います。ワンポイント解説「1.単相単巻変圧器」の通り,\( \ V_{\mathrm {m}} \ \)の電圧となる巻線の名称は直列巻線となります。
(2)解答:ヘ
題意より,解答候補は(ロ)分布容量,(ヘ)自己容量,(チ)短絡容量,となると思います。ワンポイント解説「1.単相単巻変圧器」の通り,\( \ S_{\mathrm {S}} \ \)は自己容量と呼びます。
(3)解答:ト
題意より,解答候補は(ト)\(1\),(リ)\(\sqrt {3}\),(ヨ)\(\sqrt {2}\),となると思います。自己容量\( \ S_{\mathrm {S}} \ \)と線路容量\( \ S_{\mathrm {L}} \ \)はそれぞれ,
\[
\begin{eqnarray}
S_{\mathrm {S}}&=&V_{\mathrm {m}}I_{\mathrm {h}} \\[ 5pt ]
S_{\mathrm {L}}&=&V_{\mathrm {h}}I_{\mathrm {h}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,その比は,
\[
\begin{eqnarray}
\frac {S_{\mathrm {L}}}{S_{\mathrm {S}}}&=&\frac {V_{\mathrm {h}}}{V_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {h}}}{V_{\mathrm {h}}-V_{\mathrm {l}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,\( \ V_{\mathrm {h}} \ \)に対する\( \ V_{\mathrm {l}} \ \)の比が\( \ 1 \ \)に近いほど,自己容量に対して線路容量は大きくなります。
(4)解答:イ
図3及びワンポイント解説「2.余弦定理」より,三角形\( \ v \ \),\( \ w \ \),\( \ W \ \)に余弦定理を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {l}}^{2}&=&V_{\mathrm {m}}^{2}+V_{\mathrm {n}}^{2}-2V_{\mathrm {m}}V_{\mathrm {n}}\cos 60° \\[ 5pt ]
&=&\left( V_{\mathrm {m}}+V_{\mathrm {n}}\right) ^{2}-2V_{\mathrm {m}}V_{\mathrm {n}}-2V_{\mathrm {m}}V_{\mathrm {n}}\times \frac {1}{2} \\[ 5pt ]
&=&V_{\mathrm {h}} ^{2}-3V_{\mathrm {m}}V_{\mathrm {n}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ホ
図2の線路容量\( \ S_{\mathrm {L}} \ \)は,三相変圧器であるから,
\[
\begin{eqnarray}
S_{\mathrm {L}}&=&\sqrt {3}V_{\mathrm {h}}I_{\mathrm {h}} \\[ 5pt ]
&=&\sqrt {3}V_{\mathrm {l}}I_{\mathrm {l}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ S_{\mathrm {S}} \ \)は⑥の通りとなるので,
\[
\begin{eqnarray}
K &=&\frac {S_{\mathrm {S}}}{S_{\mathrm {L}}}\\[ 5pt ]
&=&\frac {\displaystyle 3\frac {V_{\mathrm {m}}V_{\mathrm {n}}I_{\mathrm {l}}}{V_{\mathrm {h}}}}{\sqrt {3}V_{\mathrm {l}}I_{\mathrm {l}}}\\[ 5pt ]
&=&\frac {\sqrt {3}V_{\mathrm {m}}V_{\mathrm {n}}}{V_{\mathrm {h}}V_{\mathrm {l}}}\\[ 5pt ]
\end{eqnarray}
\]
となり,④より,
\[
\begin{eqnarray}
V_{\mathrm {l}}^{2}&=&V_{\mathrm {h}} ^{2}-3V_{\mathrm {m}}V_{\mathrm {n}} \\[ 5pt ]
V_{\mathrm {m}}V_{\mathrm {n}}&=&\frac {V_{\mathrm {h}}^{2}-V_{\mathrm {l}}^{2}}{3} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
K &=&\frac {\sqrt {3}V_{\mathrm {m}}V_{\mathrm {n}}}{V_{\mathrm {h}}V_{\mathrm {l}}}\\[ 5pt ]
&=&\frac {\displaystyle \sqrt {3}\frac {V_{\mathrm {h}}^{2}-V_{\mathrm {l}}^{2}}{3}}{V_{\mathrm {h}}V_{\mathrm {l}}}\\[ 5pt ]
&=&\frac {V_{\mathrm {h}}^{2}-V_{\mathrm {l}}^{2}}{\sqrt {3}V_{\mathrm {h}}V_{\mathrm {l}}}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん