【問題】
【難易度】★★★☆☆(普通)
次の文章は,机上面の平均照度と照明率の算出に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
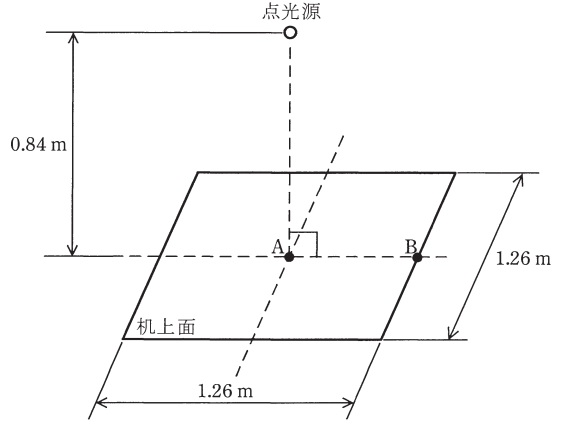
図に示すように\( \ 1 \ \)辺\( \ \mathrm {1.26 \ m} \ \)の正方形の机があり,その中央上の高さ\( \ \mathrm {0.84 \ m} \ \)に点光源が1灯設置されている。点光源の光度は,全ての方向に\( \ \mathrm {70 \ cd} \ \)である。
この条件において,以下の手順で机上面の平均照度及び照明率の算出を行う。
a 机上面中央\( \ \mathrm {A} \ \)点の水平面照度を求めると\( \ \fbox { (1) } \ \)\(\mathrm {lx} \ \)になる。
b 机上面サイドライン中央\( \ \mathrm {B} \ \)点の水平面照度を求めると\( \ \fbox { (2) } \ \)\(\mathrm {lx} \ \)になる。
c 机上面の平均照度を\( \ 5 \ \)点法で求めると\( \ \fbox { (3) } \ \)\(\mathrm {lx} \ \)になる。
d 点光源の全光束を計算すると\( \ \fbox { (4) } \ \)\(\mathrm {lm} \ \)が求まる。
e 点光源の机上面に対する照明率は,全光束と平均照度とから\( \ \fbox { (5) } \ \)となる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 0.11 &(ロ)& 0.12 &(ハ)& 0.14 \\[ 5pt ]
&(ニ)& 51 &(ホ)& 60 &(ヘ)& 63 \\[ 5pt ]
&(ト)& 67 &(チ)& 70 &(リ)& 75 \\[ 5pt ]
&(ヌ)& 79 &(ル)& 83 &(ヲ)& 99 \\[ 5pt ]
&(ワ)& 220 &(カ)& 440 &(ヨ)& 880 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
照明の勉強をしていて,公式を理解していれば確実に解ける問題ですが,1問間違えると後半の問題も間違えてしまうため,受験生の点数差をつける非常に厳しい問題とも言えます。(3)の\( \ 5 \ \)点法がカギとなりそうです。
1.逆\( \ 2 \ \)乗の法則
照度\( \ E \ \)と光度\( \ I \ \)と光源からの距離\( \ l \ \)の間に,
\[
E=\frac {I}{l^{2}}
\]
が成立するという法則です。
2.水平面照度
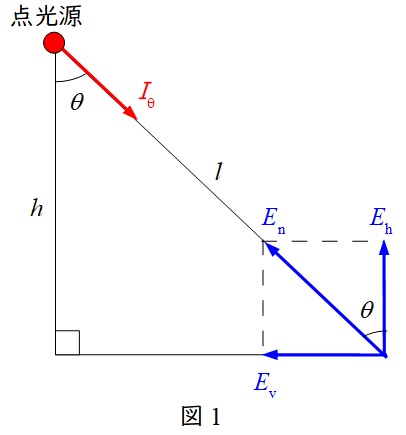
図1における\( \ E_{\mathrm {n}} \ \)を法線照度,\( \ E_{\mathrm {h}} \ \)を水平面照度と言い,以下のような関係があります。
\[
E_{\mathrm {n}}=\frac {I_{\theta }}{l^{2}}
\]
\[
E_{\mathrm {h}}=E_{\mathrm {\mathrm {n}}}\cos\theta =\frac {I_{\theta }\cos\theta }{l^{2}}
\]
3.\( \ 5 \ \)点法
問題の\( \ \mathrm {A} \ \)点の水平面照度を\( \ E_\mathrm {A} \ \),\( \ \mathrm {B} \ \)点の水平面照度を\( \ E_\mathrm {B} \ \)とした時,机上面の平均照度\( \ E_\mathrm {av} \ \)は,
\[
E_\mathrm {av}=\frac {1}{6}\left( 2E_\mathrm {A}+4E_\mathrm {B}\right)
\]
で求められます。
【解答】
(1)解答:ヲ
ワンポイント解説「1.逆\( \ 2 \ \)乗の法則」より,\( \ \mathrm {A} \ \)点の水平面照度\( \ E_\mathrm {A} \ \)は,
\[
\begin{eqnarray}
E_\mathrm {A}&=&\frac {70}{0.84^{2}} \\[ 5pt ]
&≒&99.21 → 99 \ [ \mathrm {lx} ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
点光源から\( \ \mathrm {B} \ \)点までの距離\( \ l \ \)は,
\[
\begin{eqnarray}
l&=&\sqrt {0.84^{2}+0.63^{2}} \\[ 5pt ]
&=&1.05 \ [ \mathrm {m} ]
\end{eqnarray}
\]
であるから,ワンポイント解説「2.水平面照度」より,\( \ \mathrm {B} \ \)点の水平面照度\( \ E_\mathrm {B} \ \)は,
\[
\begin{eqnarray}
E_\mathrm {B}&=&\frac {70\times \frac {0.84}{1.05}}{1.05^{2}} \\[ 5pt ]
&≒&50.79 → 51 \ [ \mathrm {lx} ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
ワンポイント解説「3.\( \ 5 \ \)点法」より机上面の平均照度\( \ E_\mathrm {av} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {av}}&=&\frac {1}{6}\left( 2E_{\mathrm {A}}+4E_{\mathrm {B}}\right) \\[ 5pt ]
&=&\frac {1}{6}\times \left( 2\times 99.21+4\times 50.79\right) \\[ 5pt ]
&=&66.93 → 67 \ [ \mathrm {lx} ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
球の立体角は\( \ 4\pi \ \)であるから,全光束\( \ F \ \)は
\[
\begin{eqnarray}
F&=&4\pi \times 70 \\[ 5pt ]
&≒&879.6 → 880 \ [ \mathrm {lm} ]
\end{eqnarray}
\]
と求められる。
(5)解答:ロ
(3)の平均照度から机上面に到達する光束量\( \ F_{\mathrm {T}} \ \)は,
\[
\begin{eqnarray}
F_{\mathrm {T}}&=&E_\mathrm {av}\times 1.26^{2} \\[ 5pt ]
&=&66.93\times 1.26^{2} \\[ 5pt ]
&≒&106.3 \ [ \mathrm {lm} ]
\end{eqnarray}
\]
となるので照明率\( \ U \ \)は,
\[
\begin{eqnarray}
U&=&\frac {F_{\mathrm {T}}}{F} \\[ 5pt ]
&=&\frac {106.3}{879.6} \\[ 5pt ]
&≒&0.12
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん