《機械》〈回転機〉[H30:問5]かご形誘導電動機の始動時異常現象に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，かご形誘導電動機の始動時異常現象に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

かご形多相誘導電動機を直入始動するとき，速度の低い領域で，それ以上加速しないで，電流が大きい状態でとどまることがある。この現象を$ \ \fbox {　（１）　} \ $現象という。

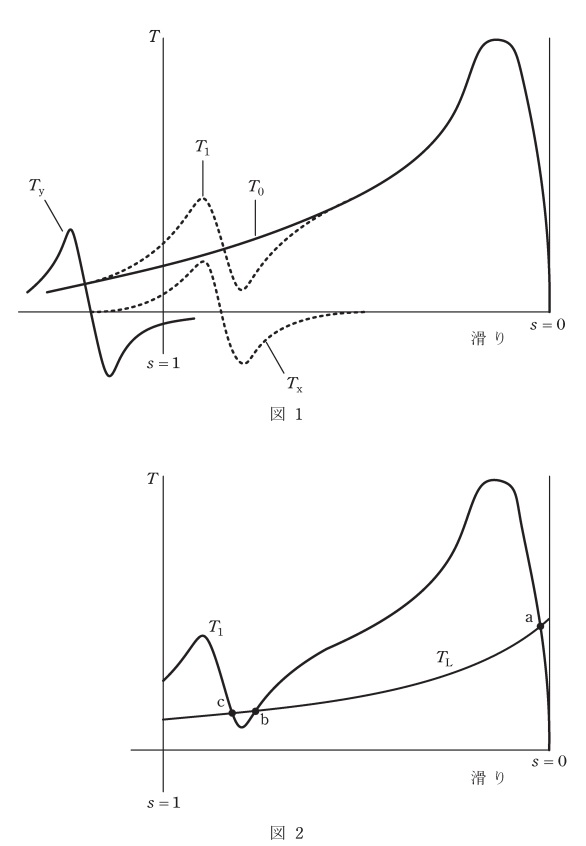
固定子起磁力の基本波は，同期速度で回転し，回転子起磁力との間に図1に示すトルク$ \ T_{0} \ $を発生する。ところが，固定子起磁力の$ \ \fbox {　（２）　} \ $のうち，第$ \ \fbox {　（３）　} \ $調波の成分は基本波と同方向に回転し，回転子に電流を誘導して図1に示すトルク$ \ T_{\mathrm {x}} \ $を発生する。これが$ \ T_{0} \ $に重畳され，合成トルクは$ \ T_{1} \ $のようになる。負荷トルクを図2に示す$ \ T_{\mathrm {L}} \ $とすると，両曲線の交点が運転点となる。始動の場合，まず，図2の三つの交点のうちで$ \ \fbox {　（４）　} \ $が運転点となるので，それ以上速度は上がらないことになる。

固定子起磁力の第$ \ \fbox {　（５）　} \ $調波は基本波と反対方向に回転するので，その発生トルクは，図1に示す$ \ T_{\mathrm {y}} \ $になる。この場合，発生トルクが正になるのは$ \ \fbox {　（６）　} \ $なので，$ \ \fbox {　（１）　} \ $現象の原因とはならない。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　5　　　　　&（ロ）&　基本波　　　　　&（ハ）&　s＜1の領域 \\[ 5pt ] &（ニ）&　\mathrm {a}　　　　　&（ホ）&　自己励磁　　　　　&（ヘ）&　2 \\[ 5pt ] &（ト）&　7　　　　　&（チ）&　時間高調波　　　　　&（リ）&　トローリング \\[ 5pt ] &（ヌ）&　奇数次　　　　　&（ル）&　偶数次　　　　　&（ヲ）&　\mathrm {c} \\[ 5pt ] &（ワ）&　空間高調波　　　　　&（カ）&　クローリング　　　　　&（ヨ）&　\mathrm {b} \\[ 5pt ] &（タ）&　s=0のとき　　　　　&（レ）&　s＞1の領域　　　　　&（ソ）&　3 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

クローリング現象をしっかりと理解するためには専門書を読んで，数式を読み解く必要があります。電験一種でもそこまで深い内容は問われないので，時間効率を考えると試験対策としては下記に記載の数式の概要を何となく理解して，現象を暗記しておく方が良いと思います。

1.空間高調波が含まれる際の回転磁界
$ \ \mathrm {a} \ $相を基準として，各相から発生された起磁力を，
\[
\begin{eqnarray}
F_{\mathrm {a}}&=&F\cos \omega t \\[ 5pt ] F_{\mathrm {b}}&=&F\cos \left( \omega t-\frac {2}{3}\pi \right) \\[ 5pt ] F_{\mathrm {c}}&=&F\cos \left( \omega t-\frac {4}{3}\pi \right) \\[ 5pt ] \end{eqnarray}
\] と置きます。第$ \ k \ $空間高調波による影響を考慮すると，
\[
\begin{eqnarray}
F_{\mathrm {ak}}&=&F\cos \omega t \sin k \theta \\[ 5pt ] F_{\mathrm {bk}}&=&F\cos \left( \omega t-\frac {2}{3}\pi \right) \sin k \left( \theta-\frac {2}{3}\pi \right) \\[ 5pt ] F_{\mathrm {ck}}&=&F\cos \left( \omega t-\frac {4}{3}\pi \right) \sin k \left( \theta-\frac {4}{3}\pi \right) \\[ 5pt ] \end{eqnarray}
\] となり，加法定理$ \ \sin \left( \alpha ±\beta \right) =\sin \alpha \cos \beta ±\cos \alpha \sin \beta \ $の関係より，
\[
\begin{eqnarray}
\cos \alpha \sin \beta &=&\frac {1}{2}\left[ \sin \left( \alpha +\beta \right) -\sin \left( \alpha -\beta \right) \right] \\[ 5pt ] \end{eqnarray}
\] が成り立つから，
\[
\begin{eqnarray}
F_{\mathrm {ak}}&=&\frac {F}{2}\left[ \sin \left( \omega t +k \theta \right) -\sin \left( \omega t -k \theta \right) \right] \\[ 5pt ] F_{\mathrm {bk}}&=&\frac {F}{2}\left[ \sin \left\{ \omega t-\frac {2}{3}\pi +k \left( \theta-\frac {2}{3}\pi \right) \right\} -\sin \left\{ \omega t-\frac {2}{3}\pi -k \left( \theta-\frac {2}{3}\pi \right) \right\} \right] \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {2}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {2}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] F_{\mathrm {ck}}&=&\frac {F}{2}\left[ \sin \left\{ \omega t-\frac {4}{3}\pi +k \left( \theta-\frac {4}{3}\pi \right) \right\} -\sin \left\{ \omega t-\frac {4}{3}\pi -k \left( \theta-\frac {4}{3}\pi \right) \right\} \right] \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {4}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {4}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] \end{eqnarray}
\] となります。それぞれの起磁力を足し合わせると，
\[
\begin{eqnarray}
F_{\mathrm {k}}&=&F_{\mathrm {ak}}+F_{\mathrm {bk}}+F_{\mathrm {ck}} \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left( \omega t +k \theta \right) -\sin \left( \omega t -k \theta \right) \right]+\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {2}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {2}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] &&+\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {4}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {4}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left( \omega t +k \theta \right)+\sin \left\{ \omega t+k\theta -\frac {2}{3}\left( 1+k \right) \pi \right\} +\sin \left\{ \omega t+k\theta -\frac {4}{3}\left( 1+k \right) \pi \right\} \right] \\[ 5pt ] &&-\frac {F}{2}\left[ \sin \left( \omega t -k \theta \right)+\sin \left\{ \omega t-k\theta -\frac {2}{3}\left( 1-k \right) \pi \right\} +\sin \left\{ \omega t-k\theta -\frac {4}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] \end{eqnarray}
\] と整理できます。上式は第一項が逆方向成分，第二項が順方向成分になることがわかります。$ \ k=7，13，・・・ \ $を代入すると，第一項の逆方向成分が零となり順方向の回転磁界が発生し，$ \ k=5，11，・・・ \ $を代入すると，第二項の順方向成分が零となり逆方向の回転磁界が発生し，$ \ k=3，9，・・・ \ $を代入すると，第一項，第二項とも零となり，回転磁界が発生しないことが分かります。

【解答】

(1)解答：カ
題意より，解答候補は（ホ）自己励磁，（リ）トローリング，（カ）クローリング，となると思います。文章はクローリング現象そのものの説明となっています。自己励磁現象は無励磁で定格速度で運転している同期発電機に、無負荷の送電線などの容量性負荷を接続した場合、残留磁気による電圧が進み電流を生じさせ、電機子反作用の磁化作用により、この電流がさらに端子電圧を高めて進み電流を増加させ、端子電圧は極限値に達して安定する現象で，二種でもよく出題された内容と思います。トローリングは聞いたことがありません。

(2)解答：ワ
題意より，解答候補は（ロ）基本波，（チ）時間高調波，（ワ）空間高調波，となると思います。固定子起磁力で発生する高調波は空間高調波と呼ばれ，一般的な高調波は時間高調波となり，ワンポイント解説「1.空間高調波が含まれる際の回転磁界」の通り，計算の考え方が異なります。

(3)解答：ト
題意より，解答候補は（イ）$ \ 5 \ $，（ヘ）$ \ 2 \ $，（ト）$ \ 7 \ $，（ヌ）奇数次，（ル）偶数次，（ソ）$3$，となると思います。ワンポイント解説「1.空間高調波が含まれる際の回転磁界」の通り，基本波と同方向の回転磁界が発生するのは第$ \ 7 \ $調波，第$ \ 13 \ $調波，・・・となります。

(4)解答：ヲ
題意より，解答候補は（ニ）$ \ \mathrm {a} \ $，（ヲ）$ \ \mathrm {c} \ $，（ヨ）$ \ \mathrm {b} \ $となると思います。このうち，$ \ \mathrm {a} \ $は本来の運転時の状態ですが，$ \ \mathrm {b} \ $は不安定な状態，$ \ \mathrm {c} \ $がクローリング現象の状態となります。

(5)解答：イ
題意より，解答候補は（イ）$ \ 5 \ $，（ヘ）$ \ 2 \ $，（ト）$ \ 7 \ $，（ヌ）奇数次，（ル）偶数次，（ソ）$ \ 3 \ $となると思います。ワンポイント解説「1.空間高調波が含まれる際の回転磁界」の通り，基本波と反対方向の回転磁界が発生するのは第$ \ 5 \ $調波，第$ \ 11 \ $調波，・・・となります。

(6)解答：レ
題意より，解答候補は（ハ）$ \ s＜1 \ $の領域，（タ）$ \ s=0 \ $のとき，（レ）$ \ s＞1 \ $の領域になると思います。図1より，明らかに交差するのは$ \ s＞1 \ $の領域になります。