【問題】
【難易度】★★☆☆☆（やや易しい）
図のような制御系について，次の問に答えよ。
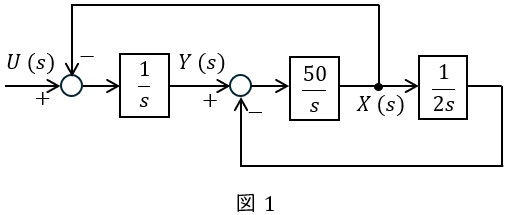
(1) 図1において，入力\( \ U (s) \ \)，内部変数\( \ X (s) \ \)，出力\( \ Y (s) \ \)の間には，次の二つの関係式が成り立つ。\( \ \mathrm {(a)} \ \)から\( \ \mathrm {(d)} \ \)までに対応する数式を答案用紙に\( \ \mathrm {(a)} \ \)から\( \ \mathrm {(d)} \ \)の記号とともに記載せよ。
\[
\begin{eqnarray}
Y(s) &=& \ \fbox {$\hskip 1em $ $(\mathrm {a})$ $\hskip 1em $} \ \left[ U(s)-X(s) \right] &・・・・・・・・・ ①& \\[ 5pt ]
X(s) &=& \ \fbox {$\hskip 1em $ $(\mathrm {b})$ $\hskip 1em $} \ \left[ Y(s)- \ \fbox {$\hskip 1em $ $(\mathrm {c})$ $\hskip 1em $} \ X(s) \right] &・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
これより，\( \ U(s) \ \)から\( \ Y(s) \ \)までの伝達関数\( \ G(s) \ \)は次式で求められる。
\[
\begin{eqnarray}
G(s) &=&\frac {Y(s)}{U(s)}= \ \fbox {$\hskip 1em $ $(\mathrm {d})$ $\hskip 1em $} &・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
(2) 図1の制御対象\( \ G (s) \ \)の共振角周波数\( \ \mathrm {[rad / s]} \ \)を求めよ。ただし，答は平方根を含む形でよい。
(3) 図1の制御対象に対して，図2に示すフィードバック制御を施すと，\( \ U(s) \ \)は，
\[
\begin{eqnarray}
U(s) &=& \ \fbox {$\hskip 1em $ $(\mathrm {e})$ $\hskip 1em $} &・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
により表される。\( \ \mathrm {(e)} \ \)に対応する数式を，\( \ f_{1} \ \)，\( \ f_{2} \ \)及び\( \ f_{3} \ \)を含む表現で答案用紙に\( \ \mathrm {(e)} \ \)の記号とともに記載せよ。
さらに，①式，②式及び④式を利用して， 目標値\( \ R(s) \ \)から出力\( \ Y (s) \ \)までの伝達関数を求めると，
\[
\begin{eqnarray}
\frac {Y(s)}{R(s)} &=& \frac { \ \fbox {$\hskip 1em $ $(\mathrm {f})$ $\hskip 1em $} \ }{s^{3}+f_{1}s^{2}+25\left( 2f_{2}+3\right) s+25\left( f_{1}+f_{3}\right) } &・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
となる。フィードバック制御により制御対象の零点を変えることができないことを利用して，\( \ \mathrm {(f)} \ \)に対応する数式を答案用紙に\( \ \mathrm {(f)} \ \)の記号とともに記載せよ。
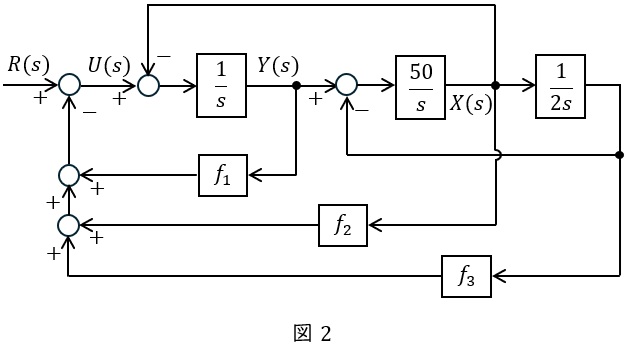
(4) 図2において，フィードバックゲインが\( \ f_{1}=9 \ \)，\( \ f_{2}=-0.5 \ \)のとき，フィードバック制御系が安定となるための\( \ f_{3} \ \)が満たすべき条件を求めよ。
【ワンポイント解説】
フィードバック制御の伝達関数に関する問題です。
少しブロック線図は複雑で計算量は多めですが，\( \ 1 \ \)種受験生ですと比較的多くの受験生が正答してくる問題です。\( \ 30 \ \)分以内を目標に解答できるよう繰り返し練習するようにしましょう。
1.ブロック線図の考え方
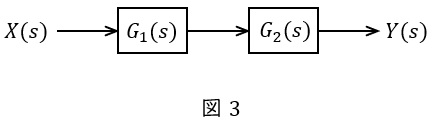
①直列
図3のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
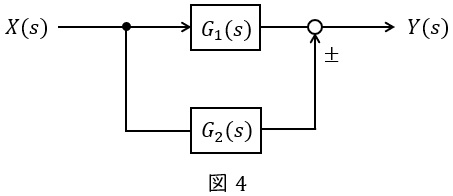
②並列
図4のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
③フィードバック
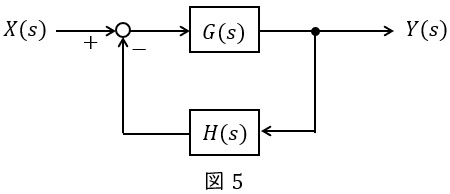
図5のような\( \ G(s) \ \)，\( \ H(s) \ \)が与えられているとき，全体の伝達関数\( \ W(s) \ \)は，
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時，ラウスの安定判別法による安定条件は，
\[
\begin{eqnarray}
&&1. s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
【解答】
(1)\( \ \mathrm {(a)} \ \)から\( \ \mathrm {(d)} \ \)までに対応する数式
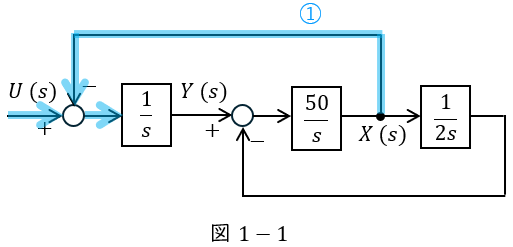
図1-1に示す関係式は，
\[
\begin{eqnarray}
Y(s) &=& \color {red}{\underline {\mathrm {(a)}\frac {1}{s}}} \left[ U(s)-X(s) \right] \\[ 5pt ]
\end{eqnarray}
\]
と求められ，図1-2に示す関係式は，
\[
\begin{eqnarray}
X(s) &=& \color {red}{\underline {\mathrm {(b)}\frac {50}{s}}} \left[ Y(s)- \color {red}{\underline {\mathrm {(c)}\frac {1}{2s}}} X(s) \right] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
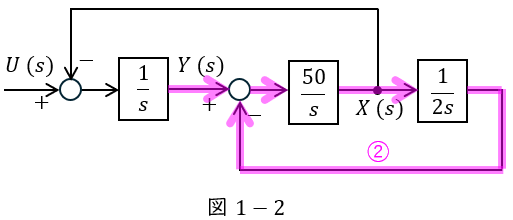
①を変形すると，
\[
\begin{eqnarray}
sY(s) &=& U(s)-X(s) \\[ 5pt ]
X(s) &=& U(s)-sY(s) &・・・・・・・・・・・・・・・・・ ①^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となるので，これを②に代入して整理すれば，
\[
\begin{eqnarray}
X(s) &=& \frac {50}{s} \left[ Y(s)- \frac {1}{2s} X(s) \right] \\[ 5pt ]
U(s)-sY(s) &=& \frac {50}{s} \left[ Y(s)- \frac {1}{2s} \left\{ U(s)-sY(s) \right\} \right] \\[ 5pt ]
\frac {s}{50}U(s)-\frac {s^{2}}{50}Y(s) &=& Y(s)- \frac {1}{2s} U(s)+\frac {1}{2}Y(s) \\[ 5pt ]
\frac {s}{50}U(s)-\frac {s^{2}}{50}Y(s) &=& \frac {3}{2}Y(s)- \frac {1}{2s} U(s) \\[ 5pt ]
\frac {s^{2}}{50}Y(s) +\frac {3}{2}Y(s)&=& \frac {s}{50}U(s)+ \frac {1}{2s} U(s) \\[ 5pt ]
\left\{ \frac {s^{2}}{50}+\frac {3}{2}\right\} Y(s) &=& \left\{ \frac {s}{50}+ \frac {1}{2s}\right\} U(s) \\[ 5pt ]
\frac {s^{2}+75}{50} Y(s) &=& \frac {s^{2}+25}{50s}U(s) \\[ 5pt ]
\left( s^{2}+75\right) Y(s) &=& \frac {s^{2}+25}{s}U(s) \\[ 5pt ]
\frac {Y(s)}{U(s)} &=& \color {red}{\underline {\mathrm {(d)}\frac {s^{2}+25}{s\left( s^{2}+75\right) }}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)制御対象\( \ G (s) \ \)の共振角周波数\( \ \mathrm {[rad / s]} \ \)
\( \ s→j\omega \ \)としたときの周波数伝達関数\( \ G (j\omega ) \ \)は，
\[
\begin{eqnarray}
G (j\omega ) &=& \frac {-\omega ^{2}+25}{j\omega \left( -\omega ^{2}+75\right) } \\[ 5pt ]
\end{eqnarray}
\]
となり，共振するのは\( \ G (j\omega ) \ \)の分母が零のときであるから，\( \ \omega ＞0 \ \)であることに注意すると，
\[
\begin{eqnarray}
-\omega ^{2}+75 &=& 0 \\[ 5pt ]
\omega ^{2} &=& 75 \\[ 5pt ]
\omega &=& 5\sqrt {3} \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {(e)} \ \)及び\( \ \mathrm {(f)} \ \)に対応する数式
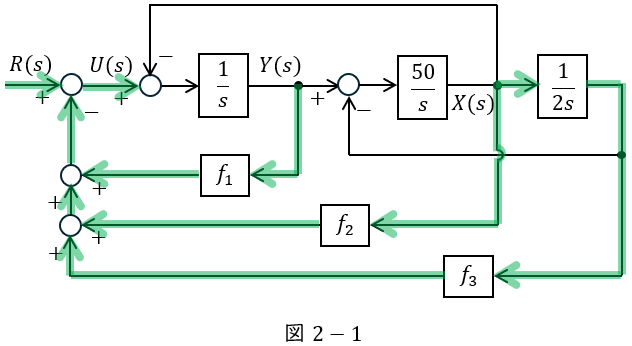
図2-1に示す関係式は，
\[
\begin{eqnarray}
U (s) &=& R (s) -\left[ f_{1}Y(s) +f_{2}X(s) +f_{3}\cdot \frac {1}{2s} X(s) \right] \\[ 5pt ]
&=& \color {red}{\underline {\mathrm {(e)}R (s) – f_{1}Y(s) -f_{2}X(s) -\frac {f_{3}}{2s} X(s)}} \\[ 5pt ]
\end{eqnarray}
\]
となり，これを\( \ ①^{\prime } \ \)に代入すると，
\[
\begin{eqnarray}
X(s) &=& U(s)-sY(s) \\[ 5pt ]
&=& R (s) – f_{1}Y(s) -f_{2}X(s) -\frac {f_{3}}{2s} X(s)-sY(s) &・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
となる。②を変形すると，
\[
\begin{eqnarray}
X(s) &=& \frac {50}{s} \left[ Y(s)- \frac {1}{2s} X(s) \right] \\[ 5pt ]
\frac {s}{50}X(s) &=& Y(s)- \frac {1}{2s} X(s) \\[ 5pt ]
\left( \frac {s}{50}+\frac {1}{2s}\right) X(s)&=& Y(s) \\[ 5pt ]
\frac {s^{2}+25}{50s}X(s)&=& Y(s) \\[ 5pt ]
X(s)&=& \frac {50s}{s^{2}+25}Y(s) \\[ 5pt ]
\end{eqnarray}
\]
となるので，これを⑥に代入すると，
\[
\begin{eqnarray}
X(s) &=& R (s) – f_{1}Y(s) -f_{2}X(s) -\frac {f_{3}}{2s} X(s)-sY(s) \\[ 5pt ]
\frac {50s}{s^{2}+25}Y(s)&=& R (s) – f_{1}Y(s) -f_{2}\cdot \frac {50s}{s^{2}+25}Y(s) -\frac {f_{3}}{2s} \cdot \frac {50s}{s^{2}+25}Y(s)-sY(s) \\[ 5pt ]
R (s)&=& \frac {50s}{s^{2}+25}Y(s) + f_{1}Y(s) +\frac {50sf_{2}}{s^{2}+25}Y(s) + \frac {25f_{3}}{s^{2}+25}Y(s)+sY(s) \\[ 5pt ]
\left( s^{2}+25\right) R (s)&=& 50sY(s) + \left( f_{1}s^{2}+25f_{1}\right) Y(s) +50sf_{2}Y(s) + 25f_{3}Y(s)+\left( s^{3}+25s\right) Y(s) \\[ 5pt ]
&=& \left\{ s^{3}+f_{1}s^{2}+\left( 50f_{2}+75\right) s+25f_{1}+25f_{3}\right\} Y(s) \\[ 5pt ]
&=& \left\{ s^{3}+f_{1}s^{2}+25\left( 2f_{2}+3\right) s+25\left( f_{1}+f_{3}\right) \right\} Y(s) \\[ 5pt ]
\frac {Y(s)}{R (s)}&=&\frac {\color {red}{\underline {\mathrm {(f)}s^{2}+25}}}{s^{3}+f_{1}s^{2}+25\left( 2f_{2}+3\right) s+25\left( f_{1}+f_{3}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ f_{1}=9 \ \)，\( \ f_{2}=-0.5 \ \)のとき，フィードバック制御系が安定となるための\( \ f_{3} \ \)が満たすべき条件
(3)解答式に\( \ f_{1}=9 \ \)，\( \ f_{2}=-0.5 \ \)を代入すると，
\[
\begin{eqnarray}
\frac {Y(s)}{R (s)}&=&\frac {s^{2}+25}{s^{3}+9s^{2}+25\left\{ 2\times \left( -0.5\right) +3\right\} s+25\left( 9+f_{3}\right) } \\[ 5pt ]
&=&\frac {s^{2}+25}{s^{3}+9s^{2}+50s+25\left( 9+f_{3}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので，特性方程式は，
\[
\begin{eqnarray}
s^{3}+9s^{2}+50s+25\left( 9+f_{3}\right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり，ラウスの数表を作成すると，ワンポイント解説「2.ラウスの安定判別法」の通り，
\[
\begin{array}{c|cc}
& 1列 & 2列 \\
\hline
1行 & 1 & 50 \\
2行 & 9 & 25\left( 9+f_{3}\right) \\
3行 & \frac {9\times 50-25\left( 9+f_{3}\right) }{9} & 0 \\
4行 & 25\left( 9+f_{3}\right) & \\
\end{array}
\]
となる。これより，安定となる条件は，\( \ 3 \ \)行\( \ 1 \ \)列の条件より，
\[
\begin{eqnarray}
\frac {9\times 50-25\left( 9+f_{3}\right) }{9} &＞&0 \\[ 5pt ]
450-25\left( 9+f_{3}\right) &＞&0 \\[ 5pt ]
25\left( 9+f_{3}\right) &＜&450 \\[ 5pt ]
9+f_{3}&＜&18 \\[ 5pt ]
f_{3}&＜&9 \\[ 5pt ]
\end{eqnarray}
\]
であり，\( \ 4 \ \)行\( \ 1 \ \)列の条件より，
\[
\begin{eqnarray}
25\left( 9+f_{3}\right) &＞&0 \\[ 5pt ]
9+f_{3} &＞&0 \\[ 5pt ]
f_{3} &＞&-9 \\[ 5pt ]
\end{eqnarray}
\]
となるので，\( \ -9＜f_{3}＜9 \ \)と求められる。
愛知県出身 愛称たけちゃん