【問題】
【難易度】★★★☆☆(普通)
ダイオードによる単相全波整流回路によって交流電圧から直流電圧を得るには次の三つの代表的な方法があり,それぞれの方法において交流電流波形は異なる。交流電圧は\( \ e=\sqrt {2}E \sin \omega t \ \mathrm {[V]} \ \)で,交流電源のインピーダンス,重なり角などを無視し,回路が定常状態にあるものとして,次の問に答えよ。
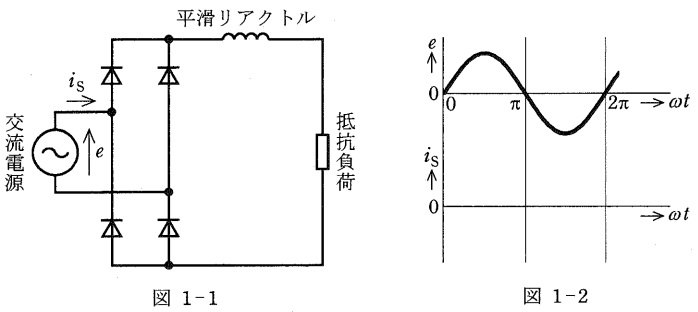
(1) 図1-1の回路において,平滑リアクトルのインダクタンスは十分に大きく,直流電流は一定とする。このとき,図1-2と同じ図が答案用紙に印刷されているので,交流電圧\( \ e \ \)の波形に対する交流電流\( \ i_{\mathrm {S}} \ \)の波形を太線で明確に描け。また,このときに抵抗負荷に印加される平均直流電圧\( \ E_{\mathrm {d1}} \ \)を \( \ E \ \)を用いた式で示せ。
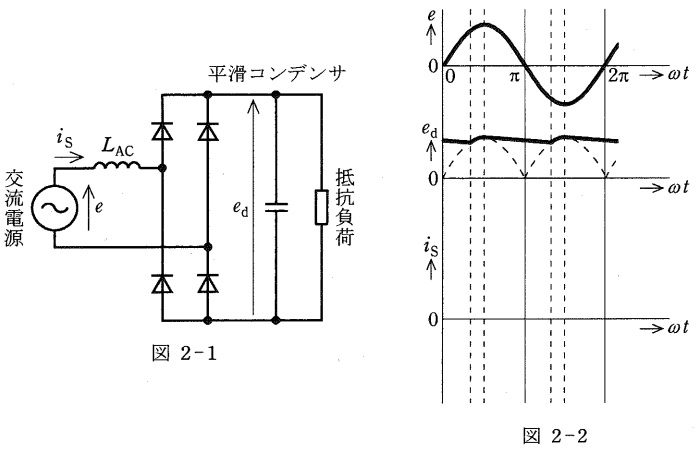
(2) 図2-1の回路において,平滑コンデンサのキャパシタンスは,交流電源からの充電電流と負荷電流とによる直流電圧\( \ e_{\mathrm {d}} \ \)の変動が図2-2に示す程度になる大きさとする。また,交流電源側に充電電流の過大なピーク値だけを抑える微小なインダクタンス\( \ L_{\mathrm {AC}} \ \)を挿入している。このとき,図2-2と同じ図が答案用紙に印刷されているので,交流電圧\( \ e \ \)及び直流電圧\( \ e_{\mathrm {d}} \ \)の波形に対する代表的な交流電流\( \ i_{\mathrm {S}} \ \)の波形を太線で明確に描け。また,抵抗負荷がないときの平均直流電圧\( \ E_{\mathrm {d2}} \ \)を\( \ E \ \)を用いた式で示し,直流電流が増加すると平均直流電圧は上昇するか,低下するかを述べよ。
(3) 図3-1の回路において,交流電圧の周波数に対して十分高い周波数でバルブデバイス\( \ \mathrm {Q} \ \)をオン,オフすることにより,直流電圧を目標値に制御しながら,同時に,交流電流の波形を力率\( \ 1 \ \)の正弦波電流基準に従って制御できることが知られている。このとき,図3-2と同じ図が答案用紙に印刷されているので,交流電圧\( \ e \ \)の波形に対する交流電流\( \ i_{\mathrm {S}} \ \)の波形の例を太線で明確に描け。また,全波整流回路の直流出力電圧\( \ e_{\mathrm {rec}} \ \)と抵抗負荷に供給される直流電圧\( \ e_{\mathrm {dc}} \ \)とを比較して,この回路が正常に動作しているときの両者の大小関係を述べよ。

【ワンポイント解説】
ダイオードを用いた単相全波整流回路に関する問題です。
(3)がなければ\( \ 1 \ \)種の問題としては非常に易しい問題となります。合格点を狙うのであれば,十分に選択する価値がある問題といえるでしょう。
1.単相ダイオードブリッジ整流回路の動作
図4,図5に示す単相ダイオードブリッジ整流回路は以下のように動作します。
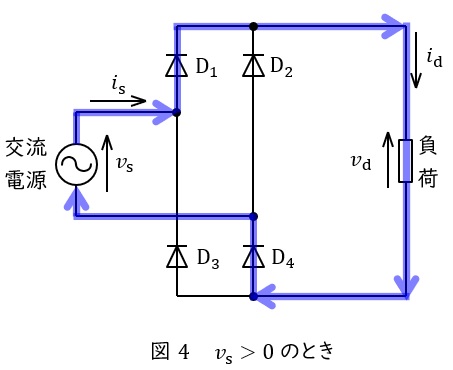
①\( \ v_{\mathrm {s}}>0 \ \)のとき
図4のように,電流は交流電源→\( \ \mathrm {D}_{1} \ \)→負荷→\( \ \mathrm {D}_{4} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると,入力電圧\( \ v_{\mathrm {s}} \ \)と等しくなります。
②\( \ v_{\mathrm {s}}<0 \ \)のとき
図5のように,電流は交流電源→\( \ \mathrm {D}_{2} \ \)→負荷→\( \ \mathrm {D}_{3} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると,\( \ -v_{\mathrm {s}} \ \)となります。

単相ダイオードブリッジ整流回路の平均出力電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は,交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると,周期\( \ \pi \ \)の波形となるため,
\[
\begin{eqnarray}
V_{\mathrm {d}} &=& \frac {1}{\pi }\int _{0}^{\pi }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=& \frac {\sqrt {2}}{\pi }V\left[ -\cos \omega t\right] _{0}^{\pi } \\[ 5pt ]
&=& \frac {\sqrt {2}}{\pi }V\left( -\cos \pi +\cos 0 \right) \\[ 5pt ]
&=& \frac {2\sqrt {2}}{\pi }V \\[ 5pt ]
&≃& 0.90V \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)交流電流\( \ i_{\mathrm {S}} \ \)の波形と平均直流電圧\( \ E_{\mathrm {d1}} \ \)
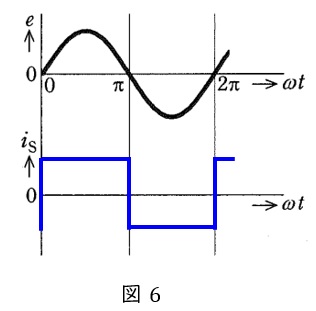
インダクタンスが十分に大きい平滑リアクトルを設置することで,抵抗負荷に流れる電流はほぼ一定になる。したがって,交流電流\( \ i_{\mathrm {S}} \ \)は,ほぼ同じ大きさの電流値が,素子が切り替わる毎に正負が入れ替わるような波形となり,図6に示すような方形波となる。
また平均直流電圧\( \ E_{\mathrm {d1}} \ \)は,ワンポイント解説「1.単相ダイオードブリッジ整流回路の動作」の通り,
\[
\begin{eqnarray}
E_{\mathrm {d1}} &=& \frac {1}{\pi }\int _{0}^{\pi }\sqrt {2}E\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=& \frac {\sqrt {2}}{\pi }E\left[ -\cos \omega t\right] _{0}^{\pi } \\[ 5pt ]
&=& \frac {\sqrt {2}}{\pi }E\left( -\cos \pi +\cos 0 \right) \\[ 5pt ]
&=& \frac {2\sqrt {2}}{\pi }E \\[ 5pt ]
&≃& 0.900E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)交流電流\( \ i_{\mathrm {S}} \ \)の波形と平均直流電圧\( \ E_{\mathrm {d2}} \ \)
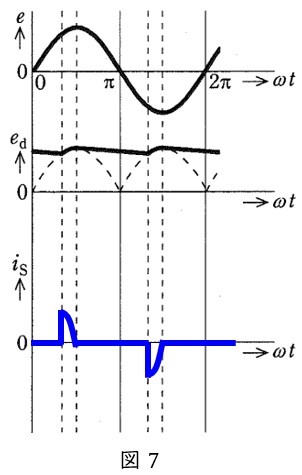
交流電流\( \ i_{\mathrm {S}} \ \)は\( \ \left| e\right| > \left| e_{\mathrm {d}}\right| \ \)のときに流れ,\( \ \left| e\right| < \left| e_{\mathrm {d}}\right| \ \)のときには流れない。したがって,\( \ i_{\mathrm {S}} \ \)の波形は図7に示すような波形となる。
平均直流電圧\( \ E_{\mathrm {d2}} \ \)は,抵抗負荷がないとすれば\( \ E_{\mathrm {d2}}=\sqrt {2}E \ \mathrm {[V]} \ \)となり,直流電流が増加するとコンデンサの充放電が発生する分だけ平均直流電圧は低下する。
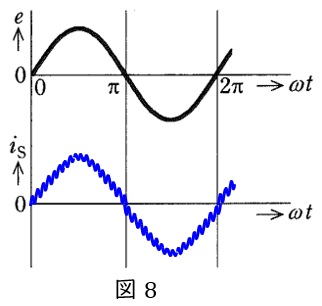
(3)交流電流\( \ i_{\mathrm {S}} \ \)の波形と全波整流回路の直流出力電圧\( \ e_{\mathrm {rec}} \ \)と抵抗負荷に供給される直流電圧\( \ e_{\mathrm {dc}} \ \)の大小関係
十分高い周波数でバルブデバイス\( \ \mathrm {Q} \ \)をオン,オフすることにより,交流電流の波形を力率\( \ 1 \ \)の正弦波電流基準に従って制御することができ,波形は図8のようになる。また,バルブデバイス\( \ \mathrm {Q} \ \)を挿入することにより,昇圧チョッパのような回路が出来上がるので,直流出力電圧\( \ e_{\mathrm {rec}} \ \)と抵抗負荷に供給される直流電圧\( \ e_{\mathrm {dc}} \ \)の大小関係は\( \ e_{\mathrm {rec}}<e_{\mathrm {dc}} \ \)となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん