【問題】
【難易度】★★★☆☆(普通)
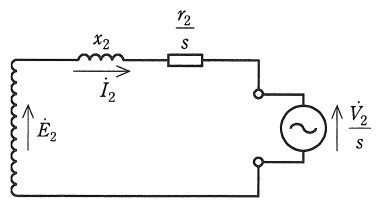
三相巻線形誘導電動機がある。図は滑り\( \ s \ \)で運転しているときの一次側に換算した二次回路\( \ 1 \ \)相分の等価回路である。この図では静止時の二次誘導起電力を\( \ {\dot E}_{2} \ \)(相電圧),二次回路の抵抗を\( \ r_{2} \ \),定格周波数における二次回路のリアクタンスを\( \ x_{2} \ \)としている。
この誘導電動機のスリップリングに滑り周波数の二次励磁電源を接続して同期速度以下の速度制御を行う。二次励磁電源の相電圧を\( \ {\dot V}_{2} \ \)とするとき,次の問に答えよ。ただし,二次励磁電源回路のインピーダンスは無視でき,また,\( \ E_{2} \ \)は\( \ {\dot E}_{2} \ \)の大きさ,\( \ V_{2} \ \)は\( \ {\dot V}_{2} \ \)の大きさを表すものとする。
(1) スリップリングを短絡し,滑り\( \ s_{0} \ \)で運転したときの同期ワットで表したトルク\( \ T_{0} \ \mathrm {[W]} \ \)を求めよ。
(2) 二次誘導起電力\( \ {\dot E}_{2} \ \)と同相の\( \ {\dot V}_{2} \ \)を図の方向に加え,滑り\( \ s \ \)で運転した。このとき,二次入力が同期ワットで表したトルクであることを示せ。
(3) 二次誘導起電力\( \ {\dot E}_{2} \ \)と同相の\( \ {\dot V}_{2} \ \)を図の方向に加え,\( \ V_{2} \ \)を調整したところ,滑りは上記(1)と同じ滑り\( \ s_{0} \ \),トルクは上記(1)のトルク\( \ T_{0} \ \)の\( \ \displaystyle \frac {1}{3} \ \)となった。\( \ V_{2} \ \)の,回転子巻線\( \ 1 \ \)相に誘導される起電力の大きさに対する比\( \ \displaystyle \frac {V_{2}}{s_{0}E_{2}} \ \)はいくらか。
【ワンポイント解説】
誘導電動機の二次回路の同期ワットの問題は頻出問題ですが,本問では二次励磁電源を接続する特殊な問題となっています。しかし,基本的には\( \ {\dot E}_{2} \ \)が\( \ \displaystyle {\dot E}_{2}-\frac {{\dot V}_{2}}{s} \ \)になるだけであり,計算はそれほど複雑にはなりません。
ちなみに,同期ワットとはあるトルク\( \ T \ \)で同期角速度\( \ \omega _{s} \ \)で回転するとした場合の出力\( \ P_{\mathrm {s}}=\omega _{\mathrm {s}}T \ \)のことを意味し,二次入力と等しくなります。
【解答】
(1)スリップリングを短絡し,滑り\( \ s_{0} \ \)で運転したときの同期ワットで表したトルク\( \ T_{0} \ \mathrm {[W]} \ \)
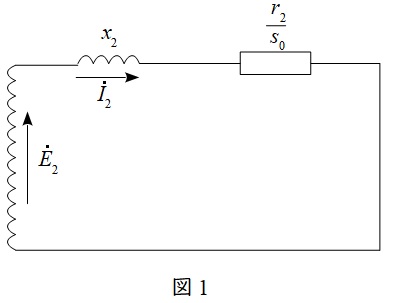
図1にスリップリングを短絡した場合の等価回路を示す。図1より,短絡時の二次電流\( \ I_{20} \ \)は,
\[
\begin{eqnarray}
I_{20}&=&\frac {E_{2}}{\displaystyle \frac {r_{2}}{s_{0}}+\mathrm {j}x_{2}} \\[ 5pt ]
&=&\frac {E_{2}}{\displaystyle \left( \frac {r_{2}}{s_{0}}\right) ^2+x_{2}^2}\left( \frac {r_{2}}{s_{0}}-\mathrm {j}x_{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるから,二次入力\( \ P_{20} \ \)は,
\[
\begin{eqnarray}
P_{20}&=&3E_{2} \cdot \mathrm {Re} \left( I_{20} \right) \\[ 5pt ]
&=&3E_{2}\frac {E_{2}}{\displaystyle \left( \frac {r_{2}}{s_{0}}\right) ^2+x_{2}^2}\left( \frac {r_{2}}{s_{0}}\right) \\[ 5pt ]
&=&\frac {3r_{2}E_{2}^{2}}{\displaystyle \frac {r_{2}^{2}}{s_{0}}+s_{0}x_{2}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。同期ワットで表したトルク\( \ T_{0} \ \)は入力\( \ P_{20} \ \)に等しいので,
\[
\begin{eqnarray}
T_{0}&=&P_{20}=\frac {3r_{2}E_{2}^{2}}{\displaystyle \frac {r_{2}^{2}}{s_{0}}+s_{0}x_{2}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)二次入力が同期ワットで表したトルクであることを示す
題意より,二次電流\( \ I_{2} \ \)は,
\[
\begin{eqnarray}
I_{2}&=&\frac {\displaystyle E_{2}-\frac {V_{2}}{s}}{\displaystyle \frac {r_{2}}{s}+\mathrm {j}x_{2}} \\[ 5pt ]
&=&\frac {\displaystyle E_{2}-\frac {V_{2}}{s}}{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2}\left( \frac {r_{2}}{s}-\mathrm {j}x_{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるから,二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{2}&=&3E_{2} \cdot \mathrm {Re} \left( I_{2} \right) \\[ 5pt ]
&=&3E_{2}\frac {\displaystyle E_{2}-\frac {V_{2}}{s}}{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2}\left( \frac {r_{2}}{s}\right) \\[ 5pt ]
&=&\frac {\displaystyle 3\frac {r_{2}}{s}E_{2}\left( E_{2}-\frac {V_{2}}{s}\right) }{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2} \\[ 5pt ]
\end{eqnarray}
\]
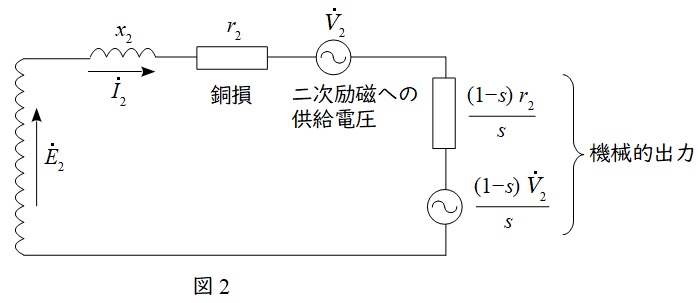
となる。題意の等価回路は図2のように書き換えられ,この時の二次銅損\( \ P_{\mathrm {c}} \ \)及び二次励磁電源へ供給される電力\( \ P_{\mathrm {V}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {c}}&=&3r_{2}I_{2}^{2} \\[ 5pt ]
&=&3r_{2}\left( \frac {\displaystyle E_{2}-\frac {V_{2}}{s}}{\displaystyle \frac {r_{2}}{s}+\mathrm {j}x_{2}}\right)^{2} \\[ 5pt ]
&=&\frac {\displaystyle 3r_{2}\left( E_{2}-\frac {V_{2}}{s}\right) ^{2}}{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2} \\[ 5pt ]
P_{\mathrm {V}}&=&3V_{2} \cdot \mathrm {Re} \left( I_{2} \right) \\[ 5pt ]
&=&3V_{2}\frac {\displaystyle E_{2}-\frac {V_{2}}{s}}{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2}\left( \frac {r_{2}}{s}\right) \\[ 5pt ]
&=&\frac {\displaystyle 3\frac {r_{2}}{s}V_{2}\left( E_{2}-\frac {V_{2}}{s}\right) }{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2} \\[ 5pt ]
\end{eqnarray}
\]
となる。従って,出力\( \ P_{\mathrm {o}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}}&=&P_{2}-P_{\mathrm {c}}-P_{\mathrm {V}} \\[ 5pt ]
&=&\frac {\displaystyle 3\frac {r_{2}}{s}E_{2}\left( E_{2}-\frac {V_{2}}{s}\right) }{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2}-\frac {\displaystyle 3r_{2}\left( E_{2}-\frac {V_{2}}{s}\right) ^{2}}{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2}-\frac {\displaystyle 3\frac {r_{2}}{s}V_{2}\left( E_{2}-\frac {V_{2}}{s}\right) }{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2} \\[ 5pt ]
&=&\frac {\displaystyle 3r_{2}\left( E_{2}-\frac {V_{2}}{s}\right) }{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2}\left\{ \frac {E_{2}}{s}-\left( E_{2}-\frac {V_{2}}{s}\right) -\frac {V_{2}}{s}\right\} \\[ 5pt ]
&=&\frac {\displaystyle 3r_{2}\left( E_{2}-\frac {V_{2}}{s}\right) }{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2}\cdot \frac {1-s}{s}E_{2} \\[ 5pt ]
&=&\left( 1-s\right)\left\{ \frac {\displaystyle 3\frac {r_{2}}{s}E_{2}\left( E_{2}-\frac {V_{2}}{s}\right) }{\displaystyle \left( \frac {r_{2}}{s}\right) ^2+x_{2}^2} \right\} \\[ 5pt ]
&=&\left( 1-s\right) P_{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。この時の角速度を\( \ \omega \ \),同期角速度を\( \ \omega _{\mathrm {s}} \ \),トルク\( \ \displaystyle T=\frac {P_{\mathrm {o}}}{\omega} \ \)とすると,同期ワットは次のように求められる。
\[
\begin{eqnarray}
\omega _{\mathrm {s}}T&=&\omega _{\mathrm {s}}\frac {P_{\mathrm {o}}}{\omega} \\[ 5pt ]
&=&\omega _{\mathrm {s}}\frac {\left( 1-s\right) P_{2}}{\omega _{\mathrm {s}}\left( 1-s\right)} \\[ 5pt ]
&=&P_{2} \\[ 5pt ]
\end{eqnarray}
\]
すなわち,二次入力\( \ P_{2} \ \)が同期ワットで表したトルクとなる。
(3)\( \ V_{2} \ \)の,回転子巻線一相に誘導される起電力の大きさに対する比\( \ \displaystyle \frac {V_{2}}{s_{0}E_{2}} \ \)
題意より,\( \ \displaystyle P_{2}=\frac {1}{3}P_{20} \ \)となるから,
\[
\begin{eqnarray}
\frac {\displaystyle 3\frac {r_{2}}{s_{0}}E_{2}\left( E_{2}-\frac {V_{2}}{s_{0}}\right) }{\displaystyle \left( \frac {r_{2}}{s_{0}}\right) ^2+x_{2}^2}&=&\frac {1}{3}\frac {\displaystyle 3\frac {r_{2}}{s_{0}}E_{2}^{2} }{\displaystyle \left( \frac {r_{2}}{s_{0}}\right) ^2+x_{2}^2} \\[ 5pt ]
E_{2}-\frac {V_{2}}{s_{0}}&=&\frac {1}{3}E_{2} \\[ 5pt ]
\frac {V_{2}}{s_{0}E_{2}}&=&\frac {2}{3} \\[ 5pt ]
&≒&0.667 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん