【問題】
【難易度】★★★★☆(やや難しい)
図は,制御対象の出力をモデルの規範出力に追従させるサーボ系の構造を示す。この制御系について,次の問に答えよ。ただし,\( \ R\left( s \right) \ \),\( \ U_{\mathrm {R}}\left( s \right) \ \),\( \ Y_{\mathrm {R}}\left( s \right) \ \),\( \ U\left( s \right) \ \),\( \ Y\left( s \right) \ \)及び\( \ E\left( s \right) \ \)は,規範目標値\( \ r\left( t \right) \ \),規範入力\( \ u_{\mathrm {R}}\left( t \right) \ \),規範出力\( \ y_{\mathrm {R}}\left( t \right) \ \),制御入力\( \ u\left( t \right) \ \),出力\( \ y\left( t \right) \ \)及び偏差\( \ e\left( t \right) \ \)をそれぞれラプラス変換したものであり,\( \ G_{\mathrm {M}}\left( s \right) \ \)はモデルの伝達関数,\( \ G\left( s \right) \ \)は制御対象の伝達関数,\( \ K_{\mathrm {A}}\left( s \right) \ \)及び\( \ K_{\mathrm {B}}\left( s \right) \ \)はそれぞれの補償器の伝達関数を表す。
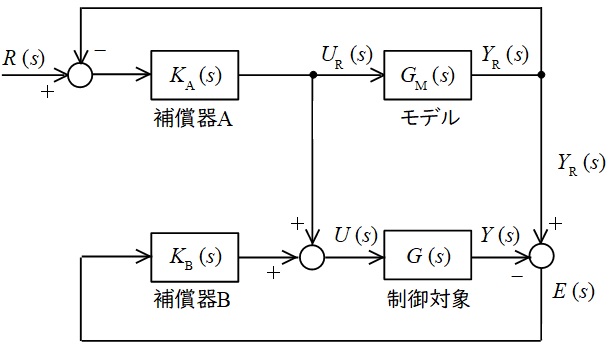
(1) \( \ R\left( s \right) \ \)から\( \ Y_{\mathrm {R}}\left( s \right) \ \)までの伝達関数を求めよ。
(2) \( \ R\left( s \right) \ \)から\( \ E\left( s \right) \ \)までの伝達関数を求めよ。
(3) 図において,それぞれの伝達関数が,\( \ G_{\mathrm {M}}\left( s \right) =\displaystyle \frac {1}{J_{\mathrm {M}}s^{2}} \ \),\( \ G\left( s \right) =\displaystyle \frac {1}{Js^{2}} \ \),\( \ K_{\mathrm {A}}\left( s \right) =K_{1}+K_{2}s \ \),\( \ K_{\mathrm {B}}\left( s \right) =\displaystyle K_{3}+K_{4}s+\frac {K_{5}}{s} \ \)で与えられるとき,次の問に答えよ。ただし,\( \ J_{\mathrm {M}}>0 \ \),\( \ J>0 \ \)及び\( \ K_{1}~K_{5} \ \)のすべての定数は正とする。
a. 上記(1)で求めた伝達関数から得られる図の上部のフィードバック系の特性方程式を求め,安定であることを示せ。そのとき,減衰定数\( \ \zeta \ \)及び固有角周波数\( \ \omega _{\mathrm {n}} \ \)を,\( \ K_{1} \ \),\( \ K_{2} \ \),\( \ J_{\mathrm {M}} \ \)を用いてそれぞれ表せ。
b. 図のサーボ系全体が安定となるための条件を求めよ。
c. 規範目標値\( \ r\left( t \right) \ \)が時間\( \ t \ \)のべき乗\( \ r\left( t \right) =t^{n} \ \)(\( \ t≧0,n \ \)は正の整数)で与えられるとき,定常偏差が有限な値をとる最大の\( \ n \ \)とそのときの定常偏差を求めよ。ただし,ラプラス変換の公式\( \ \mathcal{L} \left\{ t^{n}\right\} =\displaystyle \frac {n!}{s^{n+1}} \ \)を利用してよい。
【ワンポイント解説】
閉ループ伝達関数を求め,安定判別する典型的な自動制御の問題です。
\( \ 1 \ \)種で古典制御から出題される場合,比較的複雑な問題が出題されやすく,本問も計算量が膨大で,相当なスピードが求められると思います。また,\( \ 1 \ \)種の場合はラウスの安定判別法が必須の知識となります。
1.解の公式による安定判別法
二次の特性方程式\( \ as^{2}+bs+c=0 \ \)の根,
\[
\begin{eqnarray}
s&=&\frac {-b±\sqrt {b^{2}-4ac}}{2a} \\[ 5pt ]
\end{eqnarray}
\]
の全ての根の実数部が負の値であるとき,安定となります。
2.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられているとき,ラウスの数表は下表にように描くことができ,\( \ 1 \ \)列の値がすべて同符号であるとき,制御系は安定であると判別できます。
\[
\begin{array}{c|ccc}
& \color {red} {1 \ 列} & 2 \ 列 & 3 \ 列 \\
\hline
1 \ 行 & \color {red} {a_{0}} & a_{2} & a_{4} & \cdots \\
2 \ 行 & \color {red} {a_{1}} & a_{3} & a_{5} & \cdots \\
3 \ 行 & \color {red} {b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4 \ 行 & \color {red} {c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \color {red} {\vdots } & \vdots &
\end{array}
\]
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)\( \ R\left( s \right) \ \)から\( \ Y_{\mathrm {R}}\left( s \right) \ \)までの伝達関数
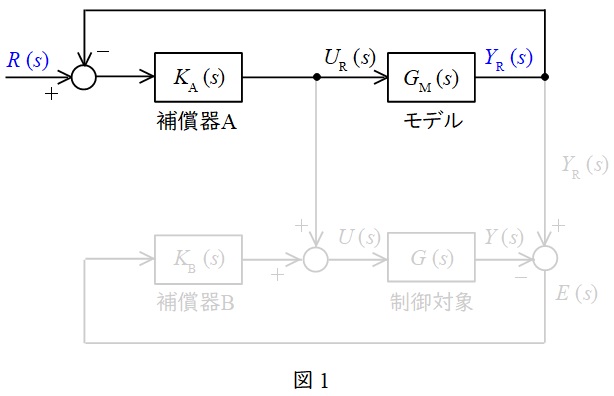
\( \ R\left( s \right) \ \)から\( \ Y_{\mathrm {R}}\left( s \right) \ \)までの伝達関数を検討する際は,図1のように制御系の上側のみを検討すれば良い。
図1より,\( \ R\left( s \right) \ \)と\( \ U_{\mathrm {R}}\left( s \right) \ \),\( \ U_{\mathrm {R}}\left( s \right) \ \)と\( \ Y_{\mathrm {R}}\left( s \right) \ \)の関係式は,
\[
\begin{eqnarray}
U_{\mathrm {R}}\left( s \right) &=&\left\{ R\left( s \right) -Y_{\mathrm {R}}\left( s \right) \right\} \cdot K_{\mathrm {A}}\left( s \right) & ・・・・・・・・・・・・・・ ①& \\[ 5pt ]
Y_{\mathrm {R}}\left( s \right) &=&U_{\mathrm {R}}\left( s \right) \cdot G_{\mathrm {M}}\left( s \right) & ・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
であるから,①を②に代入して整理すると,
\[
\begin{eqnarray}
Y_{\mathrm {R}}\left( s \right) &=&\left\{ R\left( s \right) -Y_{\mathrm {R}}\left( s \right) \right\} \cdot K_{\mathrm {A}}\left( s \right) \cdot G_{\mathrm {M}}\left( s \right) \\[ 5pt ]
Y_{\mathrm {R}}\left( s \right) &=&K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) R\left( s \right) -K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) Y_{\mathrm {R}}\left( s \right) \\[ 5pt ]
\left\{ 1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) \right\} Y_{\mathrm {R}}\left( s \right) &=&K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) R\left( s \right) \\[ 5pt ]
\frac {Y_{\mathrm {R}}\left( s \right) }{R\left( s \right) } &=&\frac {K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }{1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) } ・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ R\left( s \right) \ \)から\( E\left( s \right) \ \)までの伝達関数
(1)にて上側の制御系の伝達関数は求められており,②及び③より,
\[
\begin{eqnarray}
U_{\mathrm {R}}\left( s \right) &=&\frac {Y_{\mathrm {R}}\left( s \right) }{G_{\mathrm {M}}\left( s \right) } \\[ 5pt ]
&=&\frac {\displaystyle \frac {K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }{1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }R\left( s \right) }{G_{\mathrm {M}}\left( s \right) } \\[ 5pt ]
&=&\frac {K_{\mathrm {A}}\left( s \right) }{1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }R\left( s \right) & ・・・・・・・・・・・・・・ ④&\\[ 5pt ]
\end{eqnarray}
\]
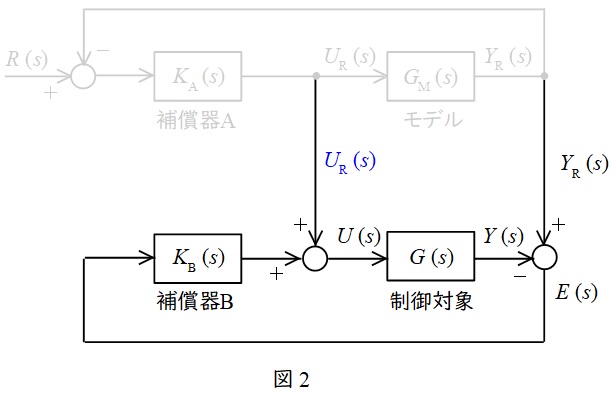
となる。これにより,図2のように下側の制御系のみ検討すれば\( \ R\left( s \right) \ \)から\( E\left( s \right) \ \)までの伝達関数が求められる。
図2より,\( \ E\left( s \right) \ \)及び\( \ U_{\mathrm {R}}\left( s \right) \ \)と\( \ U\left( s \right) \ \),\( \ U\left( s \right) \ \)と\( \ Y\left( s \right) \ \),\( \ Y_{\mathrm {R}}\left( s \right) \ \)及び\( \ Y\left( s \right) \ \)と\( \ E\left( s \right) \ \)の関係式は,
\[
\begin{eqnarray}
U\left( s \right) &=&E\left( s \right) \cdot K_{\mathrm {B}}\left( s \right) +U_{\mathrm {R}}\left( s \right) & ・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
Y\left( s \right) &=&U\left( s \right) \cdot G\left( s \right) & ・・・・・・・・・・・・・・・・ ⑥& \\[ 5pt ]
E\left( s \right) &=&-Y\left( s \right) +Y_{\mathrm {R}}\left( s \right) & ・・・・・・・・・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
となる。⑤を⑥に代入すると,
\[
\begin{eqnarray}
Y\left( s \right) &=&\left\{ E\left( s \right) \cdot K_{\mathrm {B}}\left( s \right) +U_{\mathrm {R}}\left( s \right) \right\} \cdot G\left( s \right) \\[ 5pt ]
&=&K_{\mathrm {B}}\left( s \right) G\left( s \right) E\left( s \right) + G\left( s \right) U_{\mathrm {R}}\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを⑦に代入すると,
\[
\begin{eqnarray}
E\left( s \right) &=&-\left\{ K_{\mathrm {B}}\left( s \right) G\left( s \right) E\left( s \right) + G\left( s \right) U_{\mathrm {R}}\left( s \right) \right\} +Y_{\mathrm {R}}\left( s \right) \\[ 5pt ]
\left\{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) \right\} E\left( s \right) &=&-G\left( s \right) U_{\mathrm {R}}\left( s \right) +Y_{\mathrm {R}}\left( s \right) \\[ 5pt ]
E\left( s \right) &=&-\frac {G\left( s \right) }{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) }U_{\mathrm {R}}\left( s \right) +\frac {1}{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) }Y_{\mathrm {R}}\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
と整理でき,さらに③及び④を代入すると,
\[
\begin{eqnarray}
E\left( s \right) &=&-\frac {G\left( s \right) }{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) }\frac {K_{\mathrm {A}}\left( s \right) }{1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }R\left( s \right) +\frac {1}{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) }\frac {K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }{1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }R\left( s \right) \\[ 5pt ]
&=&\frac {K_{\mathrm {A}}\left( s \right) }{\left\{ 1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) \right\} \left\{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) \right\} }\left\{ G_{\mathrm {M}}\left( s \right) -G\left( s \right) \right\} R\left( s \right) \\[ 5pt ]
\frac {E\left( s \right) }{R\left( s \right) }&=&\frac {K_{\mathrm {A}}\left( s \right) \left\{ G_{\mathrm {M}}\left( s \right) -G\left( s \right) \right\} }{\left\{ 1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) \right\} \left\{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) \right\} } ・・・・・・・ ⑧ \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)a.(1)で求めた伝達関数の特性方程式を求め,安定であることを示す。また,減衰定数\( \ \zeta \ \)及び固有角周波数\( \ \omega _{\mathrm {n}} \ \)を表す。
③にそれぞれの伝達関数を代入すると,
\[
\begin{eqnarray}
\frac {Y_{\mathrm {R}}\left( s \right) }{R\left( s \right) } &=&\frac {K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) }{1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) } \\[ 5pt ]
&=&\frac {\left( K_{1}+K_{2}s \right) \displaystyle \frac {1}{J_{\mathrm {M}}s^{2}}}{1+\left( K_{1}+K_{2}s \right) \displaystyle \frac {1}{J_{\mathrm {M}}s^{2}}} \\[ 5pt ]
&=&\frac {K_{2}s+K_{1}}{J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,特性方程式は\( \ J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}=0 \ \)となる。ワンポイント解説「1.解の公式による安定判別法」より,この特性方程式の根を求めると,
\[
\begin{eqnarray}
s &=&\frac {-K_{2}±\sqrt {K_{2}^{2}-4K_{1}J_{\mathrm {M}}}}{2J_{\mathrm {M}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。上式において\( \ K_{2}^{2}<4K_{1}J_{\mathrm {M}} \ \)の時,根の実数部は\( \ \displaystyle -\frac {K_{2}}{2J_{\mathrm {M}}}<0 \ \)となり,\( \ K_{2}^{2}>4K_{1}J_{\mathrm {M}} \ \)の時,根の実数部は\( \ \displaystyle \frac {-K_{2}±\sqrt {K_{2}^{2}-4K_{1}J_{\mathrm {M}}}}{2J_{\mathrm {M}}}<0 \ \)となるので,安定であることがわかる。
二次遅れ系の標準形は,
\[
\begin{eqnarray}
G\left( s \right) &=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,分母について伝達関数と比較すると,
\[
\begin{eqnarray}
2\zeta \omega _{\mathrm {n}} &=&\frac {K_{2}}{J_{\mathrm {M}}} \\[ 5pt ]
\omega _{\mathrm {n}}^{2} &=&\frac {K_{1}}{J_{\mathrm {M}}} → \omega _{\mathrm {n}}=\sqrt {\frac {K_{1}}{J_{\mathrm {M}}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\zeta &=&\frac {K_{2}}{J_{\mathrm {M}}}\cdot \frac {1}{2\omega _{\mathrm {n}}} \\[ 5pt ]
&=&\frac {K_{2}}{J_{\mathrm {M}}}\cdot \frac {1}{2}\sqrt {\frac {J_{\mathrm {M}}}{K_{1}}} \\[ 5pt ]
&=&\frac {K_{2}}{2\sqrt {K_{1}J_{\mathrm {M}}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)b.図のサーボ系全体が安定となるための条件
(2)解答式の⑧について,制御系の上側の安定性は評価されているので,特性方程式\( \ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) =0 \ \)が安定であれば,サーボ系全体が安定となる。それぞれの伝達関数を代入すると,
\[
\begin{eqnarray}
1+K_{\mathrm {B}}\left( s \right) G\left( s \right) &=&0 \\[ 5pt ]
1+\left( K_{3}+K_{4}s+\frac {K_{5}}{s} \right) \cdot \frac {1}{Js^{2}} &=&0 \\[ 5pt ]
1+\frac {K_{4}}{Js}+\frac {K_{3}}{Js^{2}}+\frac {K_{5}}{Js^{3}} &=&0 \\[ 5pt ]
Js^{3}+K_{4}s^{2}+K_{3}s+K_{5} &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.ラウスの安定判別法」により,ラウス表を作成すると,
\[
\begin{array}{c|cc}
& 1列 & 2列 & 3列 \\
\hline
1行 & J & K_{3} & 0 \\
2行 & K_{4} & K_{5} & 0 \\
3行 & \frac {K_{3}K_{4}-JK_{5}}{K_{4}} & 0 \\
4行 & K_{5} & \\
\end{array}
\]
となり,安定条件は\( \ K_{3}K_{4}-JK_{5}>0 \ \)と求められる。
(3)c.定常偏差が有限な値をとる最大の\( \ n \ \)とそのときの定常偏差
⑧式に各伝達関数を代入して整理すると,
\[
\begin{eqnarray}
\frac {E\left( s \right) }{R\left( s \right) }&=&\frac {K_{\mathrm {A}}\left\{ G_{\mathrm {M}}\left( s \right) -G\left( s \right) \right\} }{\left\{ 1+K_{\mathrm {A}}\left( s \right) G_{\mathrm {M}}\left( s \right) \right\} \left\{ 1+K_{\mathrm {B}}\left( s \right) G\left( s \right) \right\} } \\[ 5pt ]
&=&\frac {\left( K_{1}+K_{2}s \right) \left( \displaystyle \frac {1}{J_{\mathrm {M}}s^{2}} -\displaystyle \frac {1}{Js^{2}} \right) }{\left\{ 1+\left( K_{1}+K_{2}s \right) \displaystyle \frac {1}{J_{\mathrm {M}}s^{2}} \right\} \left\{\displaystyle 1+\left( K_{3}+K_{4}s+\frac {K_{5}}{s} \right) \cdot \frac {1}{Js^{2}} \right\} } \\[ 5pt ]
&=&\frac {\left( K_{1}+K_{2}s \right) \left( Js^{3}-J_{\mathrm {M}}s^{3}\right) }{\left( J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}\right) \left( Js^{3}+K_{4}s^{2}+K_{3}s+K_{5}\right) } \\[ 5pt ]
&=&\frac {K_{2}\left( J-J_{\mathrm {M}}\right) s^{4}+K_{1}\left( J-J_{\mathrm {M}}\right) s^{3}}{\left( J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}\right) \left( Js^{3}+K_{4}s^{2}+K_{3}s+K_{5}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「3.最終値の定理」より,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e(t)&=&\displaystyle \lim _{ s \to 0 } sE(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ s\cdot \frac {K_{2}\left( J-J_{\mathrm {M}}\right) s^{4}+K_{1}\left( J-J_{\mathrm {M}}\right) s^{3}}{\left( J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}\right) \left( Js^{3}+K_{4}s^{2}+K_{3}s+K_{5}\right) } R\left( s \right) \right] \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ \frac {K_{2}\left( J-J_{\mathrm {M}}\right) s^{5}+K_{1}\left( J-J_{\mathrm {M}}\right) s^{4}}{\left( J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}\right) \left( Js^{3}+K_{4}s^{2}+K_{3}s+K_{5}\right) } \frac {n!}{s^{n+1}} \right] \\[ 5pt ]
\end{eqnarray}
\]
となり,定常偏差が有限な値をとる\( \ n \ \)の最大値は,
\[
\begin{eqnarray}
n+1&=&4 \\[ 5pt ]
n&=&3 \\[ 5pt ]
\end{eqnarray}
\]
と求められ,そのときの定常偏差は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e(t)&=&\displaystyle \lim _{ s \to 0 } \left[ \frac {K_{2}\left( J-J_{\mathrm {M}}\right) s^{5}+K_{1}\left( J-J_{\mathrm {M}}\right) s^{4}}{\left( J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}\right) \left( Js^{3}+K_{4}s^{2}+K_{3}s+K_{5}\right) } \frac {3!}{s^{4}} \right] \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ \frac {K_{2}\left( J-J_{\mathrm {M}}\right) s+K_{1}\left( J-J_{\mathrm {M}}\right) }{\left( J_{\mathrm {M}}s^{2}+K_{2}s+K_{1}\right) \left( Js^{3}+K_{4}s^{2}+K_{3}s+K_{5}\right) } \times 6 \right] \\[ 5pt ]
&=&\frac {0+K_{1}\left( J-J_{\mathrm {M}}\right) }{\left( 0+0+K_{1}\right) \left( 0+0+0+K_{5}\right) }\times 6 \\[ 5pt ]
&=&\frac {6\left( J-J_{\mathrm {M}}\right) }{K_{5}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん