【問題】
【難易度】★★★★☆(やや難しい)
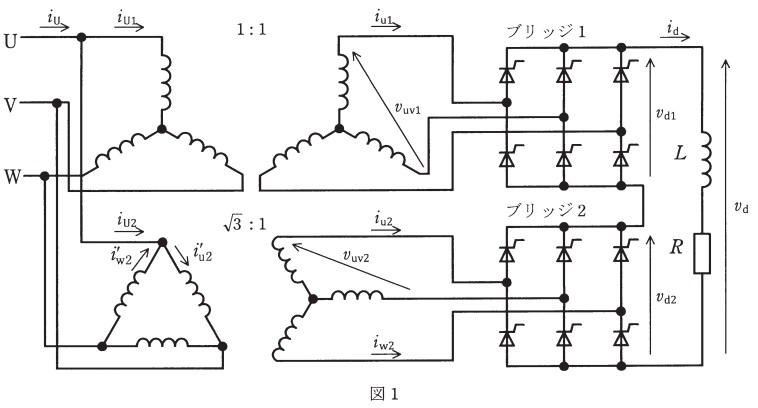
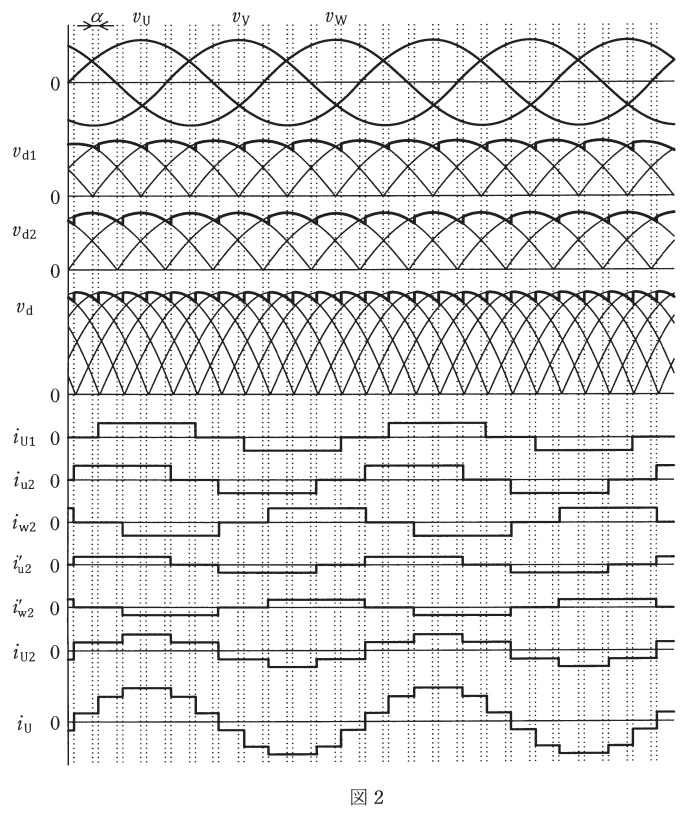
図1は12パルスサイリスタブリッジ整流器,図2は電圧電流波形である。ブリッジ1は巻数比\(1:1\)の\(\mathrm {Y-Y}\)結線した変圧器に,ブリッジ2は巻数比\(\sqrt {3}:1\)の\(\mathrm {\Delta -Y}\)結線変圧器に接続する。変圧器の一次側は線間電圧実効値が\(V [\mathrm {V}]\)の三相平衡正弦波交流電源に接続する。変圧器の漏れインダクタンスと励磁電流は十分に小さく,重なり角及びサイリスタの電圧降下は無視できるものとする。ブリッジ1及びブリッジ2の直流端子は直列に接続し,出力電圧を\(v_{\mathrm {d}} [\mathrm {V}]\)とする。ブリッジ1及びブリッジ2の制御角を\(\alpha [\mathrm {rad}]\)とする。整流器出力には,インダクタンス\(L[\mathrm {H}]\)と負荷抵抗\(R[\mathrm {\Omega }]\)を直列にして接続する。インダクタ\(L\)は十分に大きく,出力電流\(i_{\mathrm {d}} [\mathrm {A}]\)のリプルは無視でき,\(i_{\mathrm {d}}=I_{\mathrm {d}} [\mathrm {A}]\)一定として,次の問に答えよ。必要であれば,
\[
\cos \frac {\pi}{12}=\frac {\sqrt {2+\sqrt {3}}}{2}
\]
を用いてもよい。
(1) 出力電圧\(v_{\mathrm {d}}\)の平均値\(V_{\mathrm {d}}\)を\(V\)及び\(\alpha \)を用いて表せ。
(2) \(\displaystyle \alpha =\frac {\pi}{3}\)のときの出力電圧\(v_{\mathrm {d}}\)の最大値\(V_{\max}\)を求めよ。
(3) 電源電流\(i_{\mathrm {U}}[\mathrm {A}]\)の波高値\(I_{\max}\)を\(I_{\mathrm {d}}\)を用いて表せ。
(4) 電源電流\(i_{\mathrm {U}}\)の実効値\(I_{\mathrm {U}}\)を\(I_{\mathrm {d}}\)を用いて表せ。
(5) 電源電流\(i_{\mathrm {U}}\)の基本波成分の実効値\(I_{\mathrm {Uf}}\)を\(I_{\mathrm {d}}\)を用いて表せ。
(6) 高調波ひずみ率は次式で表される。
\[
高調波ひずみ率=\frac {高調波実効値}{基本波実効値}
\]
電源電流\(i_{\mathrm {U}}\)の高調波ひずみ率\(D\)を求めよ。
【ワンポイント解説】
(5)からはフーリエ級数展開を用いた計算が必要となり,全体として計算量も多いため,難しい問題となっています。本問を選択した場合,試験時間のほとんどを使用してしまい,他の問題を解くことができないかもしれません。
1.フーリエ級数展開
\(f( \theta )\)を周期\(2 \pi \)の周期関数であるとしたとき,
\[
\begin{eqnarray}
f\left( \theta \right) &=& a_{0}+\displaystyle \sum_{ n = 1 }^{ \infty } \left( a_{n} \cos n\theta + b_{n} \sin n\theta \right) \\[ 5pt ]
a_{0}&=& \frac {1}{2\pi }\int _{0}^{2\pi} f\left( \theta \right) \mathrm {d}\theta \\[ 5pt ]
a_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} f\left( \theta \right) \cos n\theta \mathrm {d}\theta \\[ 5pt ]
b_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} f\left( \theta \right) \sin n\theta \mathrm {d}\theta
\end{eqnarray}
\]
とすると,\(f( \theta )\)のフーリエ級数展開ができます。
(具体的には設問中の解答で示します。)
フーリエ級数展開について、メカニズム等もう少し詳しく知りたい方は、こちらの本で学習してみて下さい。非常に分かりやすく理解が深まると思います。
2.平均値と実効値の定義
\(f( \theta )\)を周期\(2 \pi \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\(F_{\mathrm {av}}\)
\[
F_{\mathrm {av}}=\frac {1}{2\pi }\int _{0}^{2\pi }f( \theta ) \mathrm {d}\theta
\]
②実効値\(F\)
\[
F=\sqrt {\frac {1}{2\pi} \int _{0}^{2\pi} f( \theta ) ^{2} \mathrm {d}\theta }
\]
【関連する「電気の神髄」記事】
【解答】
(1)出力電圧\(v_{\mathrm {d}}\)の平均値\(V_{\mathrm {d}}\)
出力電圧\(v_{\mathrm {d}}\)の平均値\(V_{\mathrm {d}}\)は,出力電圧\(v_{\mathrm {d1}}\)の平均値\(V_{\mathrm {d1}}\)と出力電圧\(v_{\mathrm {d2}}\)の平均値\(V_{\mathrm {d2}}\)で表すと,
\[
V_{\mathrm {d}}=V_{\mathrm {d1}}+V_{\mathrm {d2}}
\]
であり,
\[
V_{\mathrm {d1}}=V_{\mathrm {d2}}
\]
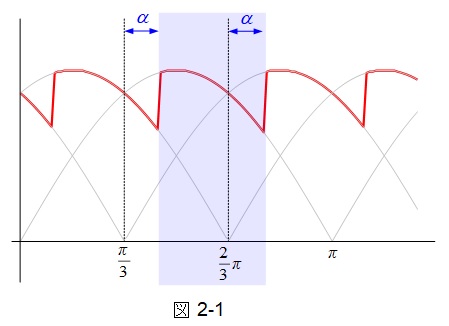
である。よって,最も求めやすい\(v_{\mathrm {d2}}\)の図2-1青範囲について平均値を求めると,
\[
\begin{eqnarray}
V_{\mathrm {d2}} &=&\frac {1}{\frac {\pi }{3}}\int _{\frac {\pi}{3}+\alpha}^{\frac {2}{3}\pi+\alpha}\sqrt {2}V\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}V \int _{\frac {\pi}{3}+\alpha}^{\frac {2}{3}\pi+\alpha}\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}V \left[ -\cos \theta \right] _{\frac {\pi}{3}+\alpha}^{\frac {2}{3}\pi+\alpha} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}V \left\{ -\cos \left( \frac {2}{3}\pi+\alpha \right) + \cos \left( \frac {\pi}{3}+\alpha \right) \right\} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}V \left( -\cos \frac {2}{3}\pi \cos \alpha + \sin \frac {2}{3}\pi \sin \alpha + \cos \frac {\pi}{3} \cos \alpha – \sin \frac {\pi}{3} \sin \alpha \right) \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}V \left( \frac {1}{2}\cos \alpha +\frac {\sqrt {3}}{2} \sin \alpha + \frac {1}{2} \cos \alpha – \frac {\sqrt {3}}{2} \sin \alpha \right) \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}V \cos \alpha
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
V_{\mathrm {d}} &=&V_{\mathrm {d1}}+V_{\mathrm {d2}} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi}V \cos \alpha+\frac {3\sqrt {2}}{\pi}V \cos \alpha \\[ 5pt ]
&=&\frac {6\sqrt {2}}{\pi}V \cos \alpha
\end{eqnarray}
\]
と求められる。
(2)\(\displaystyle \alpha =\frac {\pi}{3}\)のときの出力電圧\(v_{\mathrm {d}}\)の最大値\(V_{\max}\)
\(\displaystyle \alpha =\frac {\pi}{3}\)のときの各出力電圧\(v_{\mathrm {d1}}\),\(v_{\mathrm {d2}}\)は図2-2の通りとなる。図2-2より,出力電圧\(v_{\mathrm {d}}\)の最大値\(V_{\max}\)は,図2-2の\(\displaystyle \theta =\frac {\pi}{6},\frac {\pi}{3},\frac {\pi}{2},\frac {2}{3}\pi ・・・ \)の時であり,その大きさは,
\[
\begin{eqnarray}
V_{\max} &=&\sqrt {2}V\sin \frac {\pi}{3}+ \sqrt {2}V\sin \frac {\pi}{6} \\[ 5pt ]
&=&\sqrt {2}V\left( \frac {\sqrt {3}}{2}+\frac {1}{2}\right) \\[ 5pt ]
&=&\frac {\sqrt {2}\left( \sqrt {3}+1 \right)}{2}V
\end{eqnarray}
\]
と求められる。

(3)電源電流\(i_{\mathrm {U}}[\mathrm {A}]\)の波高値\(I_{\max}\)
各電流を\(I_{\mathrm {d}}\)で表すと,\(i_{\mathrm {u1}}\),\(i_{\mathrm {u2}}\),\(i_{\mathrm {w2}}\)の最大値は\(I_{\mathrm {d}}\)であるから,\(i_{\mathrm {u2}}^{\prime}\),\(i_{\mathrm {w2}}^{\prime}\)の最大値は\(\displaystyle \frac {I_{\mathrm {d}}}{\sqrt {3}}\)となるので,
\[
i_{\mathrm {U2}}=i_{\mathrm {u2}}^{\prime}-i_{\mathrm {w2}}^{\prime}
\]
より,\(i_{\mathrm {U2}}\)の最大値は,\(\displaystyle \frac {2I_{\mathrm {d}}}{\sqrt {3}}\)となる。
よって,電源電流\(i_{\mathrm {U}}[\mathrm {A}]\)の波高値\(I_{\max}\)は,
\[
I_{\max}=I_{\mathrm {d}}+\frac {2I_{\mathrm {d}}}{\sqrt {3}}=\left( 1+\frac {2}{\sqrt{3}}\right) I_{\mathrm {d}}
\]
と求められる。
(4)電源電流\(i_{\mathrm {U}}\)の実効値\(I_{\mathrm {U}}\)
図2より,\(i_{\mathrm {U}}\)の値は,
\begin{eqnarray}
i_{\mathrm {U}}
=
\begin{cases}
\displaystyle \frac {1}{\sqrt {3}}I_{\mathrm {d}} & ( \alpha < \theta ≦ \frac {\pi}{6}+\alpha ) \\
\displaystyle \left( 1+\frac {1}{\sqrt {3}}\right) I_{\mathrm {d}} & ( \frac {\pi}{6}+\alpha < \theta ≦ \frac {\pi}{3}+\alpha ) \\
\displaystyle \left( 1+\frac {2}{\sqrt {3}}\right) I_{\mathrm {d}} & ( \frac {\pi}{3}+\alpha < \theta ≦ \frac {\pi}{2}+\alpha )
\end{cases}
\end{eqnarray}
であり,実効値\(I_{\mathrm {U}}\)は,
\[
\begin{eqnarray}
I_{\mathrm {U}} &=&\sqrt{ \frac {1}{\pi}\int _{\alpha }^{\pi +\alpha} \left( i_{\mathrm {U}}\right) ^{2}\mathrm {d}\theta }\\[ 5pt ]
&=&\sqrt{ \frac {2}{\pi}\int _{\alpha }^{\frac {\pi}{2} +\alpha} \left( i_{\mathrm {U}}\right) ^{2}\mathrm {d}\theta }\\[ 5pt ]
&=&\sqrt{ \frac {2}{\pi}\left\{ \int _{\alpha }^{\frac {\pi}{6} +\alpha} \left( \frac {1}{\sqrt {3}}I_{\mathrm {d}}\right) ^{2}\mathrm {d}\theta +\int _{\frac {\pi}{6} +\alpha }^{\frac {\pi}{3} +\alpha} \left( \left( 1+\frac {1}{\sqrt {3}}\right) I_{\mathrm {d}}\right) ^{2}\mathrm {d}\theta +\int _{\frac {\pi}{3} +\alpha }^{\frac {\pi}{2} +\alpha} \left( \left( 1+\frac {2}{\sqrt {3}}\right) I_{\mathrm {d}}\right) ^{2}d\theta\right\} }\\[ 5pt ]
&=&\sqrt{ \frac {2}{\pi}I_{\mathrm {d}}^{2}\left\{ \int _{\alpha }^{\frac {\pi}{6} +\alpha} \frac {1}{3}\mathrm {d}\theta +\int _{\frac {\pi}{6} +\alpha }^{\frac {\pi}{3} +\alpha} \left( \frac {4}{3}+\frac {2}{\sqrt {3}}\right) \mathrm {d}\theta +\int _{\frac {\pi}{3} +\alpha }^{\frac {\pi}{2} +\alpha} \left( \frac {7}{3}+\frac {4}{\sqrt {3}}\right) \mathrm {d}\theta\right\} }\\[ 5pt ]
&=&\sqrt{ \frac {2}{\pi}I_{\mathrm {d}}^{2}\left\{ \frac {1}{3}\cdot \frac {\pi}{6} +\left( \frac {4}{3}+\frac {2}{\sqrt {3}}\right)\frac {\pi}{6} +\left( \frac {7}{3}+\frac {4}{\sqrt {3}}\right) \frac {\pi}{6}\right\} }\\[ 5pt ]
&=&\sqrt{ \frac {1}{3}I_{\mathrm {d}}^{2}\left\{ \frac {1}{3} +\left( \frac {4}{3}+\frac {2}{\sqrt {3}}\right) +\left( \frac {7}{3}+\frac {4}{\sqrt {3}}\right) \right\} }\\[ 5pt ]
&=&\sqrt{ \frac {4+2\sqrt {3}}{3}I_{\mathrm {d}}^{2}} \\[ 5pt ]
&≒&1.5774I_{\mathrm {d}} → 1.58I_{\mathrm {d}}
\end{eqnarray}
\]
と求められる。
\[
\]
(5)電源電流\(i_{\mathrm {U}}\)の基本波成分の実効値\(I_{\mathrm {Uf}}\)
ワンポイント解説「1.フーリエ級数展開」において,図2の\(\theta =\alpha \)を基準にすると,\(i_{\mathrm {U}}\)は奇関数となるため,\(a_{0}=a_{1}=0\)となり,
\[
\begin{eqnarray}
b_{1}&=& \frac {1}{\pi }\int _{0}^{2\pi} f\left( \theta \right) \sin \theta \mathrm {d}\theta \\[ 5pt ]
&=& \frac {4}{\pi }\int _{0}^{\frac {\pi}{2}} f\left( \theta \right) \sin \theta \mathrm {d}\theta \\[ 5pt ]
&=& \frac {4}{\pi }\left[ \int _{0}^{\frac {\pi}{6}} \frac {1}{\sqrt {3}}I_{\mathrm {d}} \sin \theta \mathrm {d}\theta +\int _{\frac {\pi}{6}}^{\frac {\pi}{3}} \left( 1+\frac {1}{\sqrt {3}}\right) I_{\mathrm {d}} \sin \theta \mathrm {d}\theta + \int _{\frac {\pi}{3}}^{\frac {\pi}{2}} \left( 1+\frac {2}{\sqrt {3}}\right) I_{\mathrm {d}}\sin \theta \mathrm {d}\theta\right] \\[ 5pt ]
&=& \frac {4}{\pi }I_{\mathrm {d}}\left[ \frac {1}{\sqrt {3}}\left[ -\cos \theta \right] _{0}^{\frac {\pi}{6}} +\left( 1+\frac {1}{\sqrt {3}}\right) \left[ -\cos \theta \right] _{\frac {\pi}{6}}^{\frac {\pi}{3}}+ \left( 1+\frac {2}{\sqrt {3}}\right) \left[ -\cos \theta \right] _{\frac {\pi}{3}}^{\frac {\pi}{2}}\right] \\[ 5pt ]
&=& \frac {4}{\pi }I_{\mathrm {d}}\left[ \frac {1}{\sqrt {3}}\left( -\frac {\sqrt {3}}{2}+1\right) +\left( 1+\frac {1}{\sqrt {3}}\right) \left( -\frac {1}{2}+\frac {\sqrt{3}}{2}\right) + \left( 1+\frac {2}{\sqrt {3}}\right) \frac {1}{2}\right] \\[ 5pt ]
&=& \frac {4\sqrt {3}}{\pi }I_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,基本波\(i_{\mathrm {U}}\)の基本波成分\(i_{\mathrm {Uf}}\)は,
\[
i_{\mathrm {Uf}}=\frac {4\sqrt {3}}{\pi }I_{\mathrm {d}}\sin \theta
\]
となるので,その実効値\(I_{\mathrm {Uf}}\)は,
\[
\begin{eqnarray}
I_{\mathrm {Uf}}&=& \frac {4\sqrt {3}}{\pi }I_{\mathrm {d}}\times \frac {1}{\sqrt {2}} \\[ 5pt ]
&=& \frac {4\sqrt {3}}{\sqrt {2}\pi }I_{\mathrm {d}} \\[ 5pt ]
&≒& 1.5594 I_{\mathrm {d}} → 1.56 I_{\mathrm {d}}
\end{eqnarray}
\]
と求められる。
(6)電源電流\(i_{\mathrm {U}}\)の高調波ひずみ率\(D\)
高調波成分の実効値\(I_{\mathrm {Uh}}\)は,
\[
\begin{eqnarray}
I_{\mathrm {Uh}}&=& \sqrt {I_{\mathrm {U}}^{2}-I_{\mathrm {Uf}}^{2}} \\[ 5pt ]
&=& \sqrt {\left( 1.5774I_{\mathrm {d}}\right) ^{2}-\left( 1.5594 I_{\mathrm {d}}\right) ^{2}} \\[ 5pt ]
&≒& 0.23762 I_{\mathrm {d}}
\end{eqnarray}
\]
であるから,高調波ひずみ率\(D\)は,
\[
\begin{eqnarray}
D&=& \frac {I_{\mathrm {Uh}}}{I_{\mathrm {Uf}}} \\[ 5pt ]
&=&\frac {0.23762 I_{\mathrm {d}}}{1.5594 I_{\mathrm {d}}} \\[ 5pt ]
&≒& 0.15238 → 0.153
\end{eqnarray}
\]
と求められる。























 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん