【問題】
【難易度】★★★★★(難しい)
三相円筒形同期電動機のトルク特性に関して,次の問に答えよ。
ただし,電動機の鉄心の磁気飽和は無視する。また,単位法において,電力の基準値は同期電動機の定格皮相電力\([\mathrm {kV\cdot A}]\)であり,トルクの基準値は定格回転速度での定格皮相電力相当トルク\([\mathrm {N\cdot m}]\)としている。
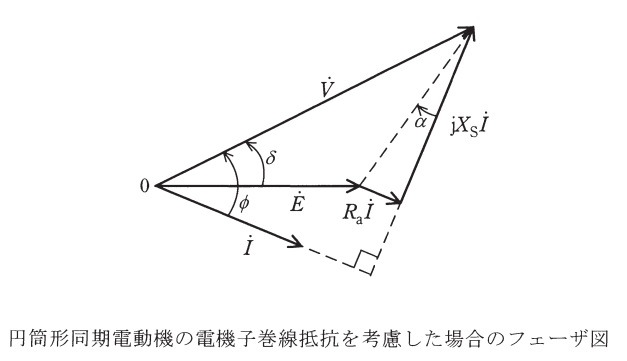
(1) 円筒形同期電動機の電機子巻線抵抗を考慮した場合のフェーザ図を示す。図において,\(\dot V\)は端子電圧(相電圧),\(\dot E\)は無負荷誘導起電力(相電圧),\(\dot I\)は相電流,\(\phi \)は力率角,\(\delta \)は内部相差角(負荷角),\(X_{\mathrm {S}}\)は同期リアクタンス,\(R_{\mathrm {a}}\)は電機子巻線抵抗,\(\alpha \)は\(\displaystyle \alpha =\tan ^{-1}\frac {R_{\mathrm {a}}}{X_{\mathrm {S}}}\)の位相角である。定格回転速度での軸出力トルク\(T [\mathrm {p.u.}]\)を\(E [\mathrm {p.u.}]\),\(V [\mathrm {p.u.}]\),同期インピーダンス\(Z_{\mathrm {S}} [\mathrm {p.u.}]\)\( (Z_{\mathrm {S}}=\sqrt {X_{\mathrm {S}}^{2}+R_{\mathrm {a}}^{2}}) \),\(\delta [\mathrm {rad}]\)及び\(\alpha [\mathrm {rad}]\)で表す式を導出せよ。ただし,電機子巻線抵抗以外の損失は無視する。
(2) 図において\(R_{\mathrm {a}}=0\mathrm {p.u.}\)及び\(\alpha = 0\mathrm {rad}\)とした場合,電機子巻線抵抗を無視した場合のフェーザ図となる。同期リアクタンス\(X_{\mathrm {S}}=1.00\mathrm {p.u.}\)及び定格力率\( ( \cos \phi ) 1.0\)の円筒形同期電動機に対して,電機子巻線抵抗を無視した場合における次の問に答えよ。また,全ての損失は無視する。
a 定格運転状態の\(E [\mathrm {p.u.}]\),\(\delta [\mathrm {rad}]\)及び\(T [\mathrm {p.u.}]\)を算出せよ。また,界磁電流,回転速度及び\(V\)が定格運転状態と同じとして,脱出トルク\(T_{\max} [\mathrm {p.u.}]\)を算出せよ。
b 負荷トルク,界磁電流及び回転速度が定格運転状態と同じままで,\(V\)が定格電圧から徐々に降下することによって,脱調が起こる\(V [\mathrm {p.u.}]\)を算出せよ。
c 界磁電流,回転速度及び\(V\)が定格運転状態と同じままで,負荷トルクが定格運転状態からステップ的に(瞬時に)\(T_{\mathrm {OL}}=1.28\mathrm {p.u.}\)に上昇したとき,\(\delta \)の最初の過渡変化によって脱調が起こるか否かを,電動機の軸出力トルク-内部相差角特性を用いて説明せよ。ただし,この過渡状態においても,電動機のリアクタンスは同期リアクタンス\(X_{\mathrm {S}}\)で扱うこととする。なお,\(\sin \theta =0.90510\)となる\(\theta \)は,\(1.1316\mathrm {rad}\)又は\(2.0100\mathrm {rad}\)とする。
【ワンポイント解説】
計算量がそれほど多くないため,元々理解しているのであれば,比較的楽に解けるかもしれませんが,初見で解いた場合内容が複雑であるため,非常に難しい問題と言えます。本問において,トルクと電力の関係が問題文に与えられていますが,解釈としては以下のような関係性となります。
1.単位法における定格回転速度でのトルク\(T [\mathrm {p.u.}]\)と電力\(P [\mathrm {p.u.}]\)の関係
単位法の定義より,
\[
\begin{eqnarray}
T [\mathrm {p.u.}]&=&\frac {T [\mathrm {N\cdot m}]}{T_{\mathrm {n}} [\mathrm {N\cdot m}]} \\[ 5pt ]
P [\mathrm {p.u.}]&=&\frac {P [\mathrm {J/s}]}{P_{\mathrm {n}} [\mathrm {J/s}]} \\[ 5pt ]
T_{\mathrm {n}} [\mathrm {N\cdot m}]&=&\frac {P_{\mathrm {n}} [\mathrm {J/s}]}{\omega _{\mathrm {n}} [\mathrm {rad/s}]} \\[ 5pt ]
\end{eqnarray}
\]
であり,定格回転速度において,
\[
T [\mathrm {N\cdot m}]=\frac {P [\mathrm {J/s}]}{\omega _{\mathrm {n}} [\mathrm {rad/s}]}
\]
であるから,
\[
\begin{eqnarray}
T [\mathrm {p.u.}]&=&\frac {T [\mathrm {N\cdot m}]}{T_{\mathrm {n}} [\mathrm {N\cdot m}]} \\[ 5pt ]
&=&\frac {\displaystyle \frac {P [\mathrm {J/s}]}{\omega _{\mathrm {n}} [\mathrm {rad/s}]}}{\displaystyle \frac {P_{\mathrm {n}} [\mathrm {J/s}]}{\omega _{\mathrm {n}} [\mathrm {rad/s}]}} \\[ 5pt ]
&=&\frac {P [\mathrm {J/s}]}{P_{\mathrm {n}} [\mathrm {J/s}]} \\[ 5pt ]
&=&P [\mathrm {p.u.}]
\end{eqnarray}
\]
という関係となり,定格回転速度においてはトルクと電力の\(\mathrm {p.u.}\)値が一致します。
【解答】
(1)定格回転速度での軸出力トルク\(T [\mathrm {p.u.}]\)
ワンポイント解説「1.単位法における定格回転速度でのトルク\(T [\mathrm {p.u.}]\)と電力\(P [\mathrm {p.u.}]\)の関係」より,定格回転速度での軸出力トルクと実出力の\(\mathrm {p.u.}\)値は一致するので,
\[
T=EI\cos \theta
\]
となる。ただし,\(\theta = \phi -\delta \)である。
フェーザ図より,
\[
\begin{eqnarray}
V\cos \delta &=&E + R_{\mathrm {a}}I\cos \theta +X_{\mathrm {S}}I\sin \theta &・・・①&\\[ 5pt ]
V\sin \delta &=& X_{\mathrm {S}}I\cos \theta – R_{\mathrm {a}}I\sin \theta &・・・②&
\end{eqnarray}
\]
の関係があるから,\( ①\times R_{\mathrm {a}} +②\times X_{\mathrm {S}}\)で\(\sin \theta \)を消去すると,
\[
\begin{eqnarray}
R_{\mathrm {a}} V\cos \delta +X_{\mathrm {S}} V\sin \delta &=&R_{\mathrm {a}} E + R_{\mathrm {a}}^{2}I\cos \theta +X_{\mathrm {S}}^{2}I\cos \theta \\[ 5pt ]
I\cos \theta &=& \frac {R_{\mathrm {a}} \left( V\cos \delta -E\right) +X_{\mathrm {S}} V\sin \delta }{R_{\mathrm {a}}^{2}+X_{\mathrm {S}}^{2}}
\end{eqnarray}
\]
となるので,トルクの式に代入すると,
\[
\begin{eqnarray}
T &=&EI\cos \theta \\[ 5pt ]
&=& E\frac {R_{\mathrm {a}} \left( V\cos \delta -E\right) +X_{\mathrm {S}} V\sin \delta }{R_{\mathrm {a}}^{2}+X_{\mathrm {S}}^{2}} \\[ 5pt ]
&=& E\frac {R_{\mathrm {a}} \left( V\cos \delta -E\right) +X_{\mathrm {S}} V\sin \delta }{Z_{\mathrm {S}}^{2}} \\[ 5pt ]
&=& \frac {E}{Z_{\mathrm {S}}}\left\{ \frac {R_{\mathrm {a}}}{Z_{\mathrm {S}}} \left( V\cos \delta -E\right) +\frac {X_{\mathrm {S}}}{Z_{\mathrm {S}}} V\sin \delta \right\} \\[ 5pt ]
&=& \frac {E}{Z_{\mathrm {S}}}\left[ \sin \alpha \left( V\cos \delta -E\right) +\cos \alpha V\sin \delta \right] \\[ 5pt ]
&=& \frac {E}{Z_{\mathrm {S}}}\left( V\sin \alpha \cos \delta -E\sin \alpha +V\cos \alpha \sin \delta \right) \\[ 5pt ]
&=& \frac {E}{Z_{\mathrm {S}}}\left( V\sin \alpha \cos \delta +V\cos \alpha \sin \delta -E\sin \alpha \right) \\[ 5pt ]
&=& \frac {E}{Z_{\mathrm {S}}}\left\{ V\sin (\alpha + \delta ) -E\sin \alpha \right\} \\[ 5pt ]
&=& \frac {EV}{Z_{\mathrm {S}}}\sin (\alpha + \delta ) -\frac {E^{2}}{Z_{\mathrm {S}}}\sin \alpha
\end{eqnarray}
\]
と求められる。
(2)a.定格運転状態の\(E [\mathrm {p.u.}]\),\(\delta [\mathrm {rad}]\)及び\(T [\mathrm {p.u.}]\)と脱出トルク\(T_{\max} [\mathrm {p.u.}]\)
題意に沿ってフェーザ図を描きなおすと図1のようになる。
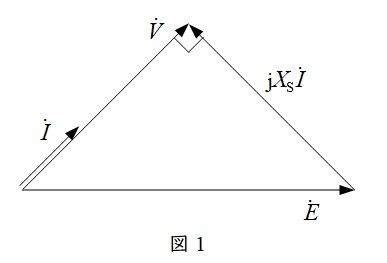
定格運転状態において\(V=1\mathrm {p.u.}\),\(I=1\mathrm {p.u.}\),\(X_{\mathrm {S}}=1\mathrm {p.u.}\)であるから,
\[
\begin{eqnarray}
E &=&\sqrt {V^{2}+ \left( X_{\mathrm {S}}I\right) ^{2}} \\[ 5pt ]
&=&\sqrt {1+1} \\[ 5pt ]
&=&\sqrt {2} \ [\mathrm {p.u.}]
\end{eqnarray}
\]
と求められる。またフェーザ図より,
\[
\sin \delta =\frac {1}{\sqrt {2}}
\]
となるので,
\[
\delta =\frac {\pi }{4} \ [\mathrm {rad}]
\]
と求められる。
(1)解答式に,\(R_{\mathrm {a}}=0\mathrm {p.u.}\)及び\(\alpha = 0\mathrm {rad}\)を代入すると,
\[
\begin{eqnarray}
T &=&\frac {EV}{Z_{\mathrm {S}}}\sin (\alpha + \delta ) -\frac {E^{2}}{Z_{\mathrm {S}}}\sin \alpha \\[ 5pt ]
&=& \frac {EV}{X_{\mathrm {S}}}\sin (0 + \delta ) -\frac {E^{2}}{X_{\mathrm {S}}}\sin 0 \\[ 5pt ]
&=& \frac {EV}{X_{\mathrm {S}}}\sin \delta
\end{eqnarray}
\]
となるので,各値を代入すると,
\[
\begin{eqnarray}
T &=&\frac {\sqrt {2}\times 1}{1}\times \frac {1}{\sqrt {2}} \\[ 5pt ]
&=& 1 \ [\mathrm {p.u.}]
\end{eqnarray}
\]
と求められる。
界磁電流,回転速度及び\(V\)が定格運転状態と同じとした時の脱出トルク\(T_{\max} [\mathrm {p.u.}]\)は,\(\sin \delta=1\)の時であるから,
\[
\begin{eqnarray}
T_{\max} &=&\frac {EV}{X_{\mathrm {S}}}\sin \delta \\[ 5pt ]
&=& \frac {\sqrt {2}\times 1}{1}\times 1 \\[ 5pt ]
&=& \sqrt {2} \ [\mathrm {p.u.}]
\end{eqnarray}
\]
と求められる。
(2)b.脱調が起こる\(V [\mathrm {p.u.}]\)
負荷トルク,界磁電流及び回転速度が定格運転状態と同じままである時,
\[
\begin{eqnarray}
T &=&\frac {EV}{X_{\mathrm {S}}}\sin \delta \\[ 5pt ]
1 &=&\frac {\sqrt {2}V}{1}\sin \delta \\[ 5pt ]
\sin \delta &=&\frac {1}{\sqrt {2}V}
\end{eqnarray}
\]
であり,脱調が起こるのは\(\sin \delta > 1\)になった時である。よって脱調が起こる電圧\(V\)は,
\[
\begin{eqnarray}
\frac {1}{\sqrt {2}V} &>&1 \\[ 5pt ]
V &<&\frac {1}{\sqrt {2}} \ [\mathrm {p.u.}]
\end{eqnarray}
\]
と求められる。
(2)c.過渡変化によって脱調が起こるか否か
(2)aより定格運転状態の時,\(E=\sqrt {2}\mathrm {p.u.}\),\(V=1\mathrm {p.u.}\),\(X_{\mathrm {S}}=1\mathrm {p.u.}\),\(T=1 \mathrm {p.u.}\),\(\displaystyle \delta =\frac {\pi }{4}\mathrm {rad}\)であり,\(T_{\mathrm {OL}}=1.28\mathrm {p.u.}\)に上昇したときは,
\[
\begin{eqnarray}
T_{\mathrm {OL}} &=&\frac {EV}{X_{\mathrm {S}}}\sin \delta_{\mathrm {OL}} \\[ 5pt ]
1.28 &=&\sqrt {2}\sin \delta_{\mathrm {OL}} \\[ 5pt ]
\sin \delta_{\mathrm {OL}} &=&\frac {1.28}{\sqrt {2}}\\[ 5pt ]
&≒&0.90510
\end{eqnarray}
\]
となり,題意より\(\delta_{\mathrm {OL}} =1.1316 \mathrm {rad},2.0100 \mathrm {rad}\)と求められる。
よって,電動機の軸出力トルク-内部相差角特性は図2のようになる。
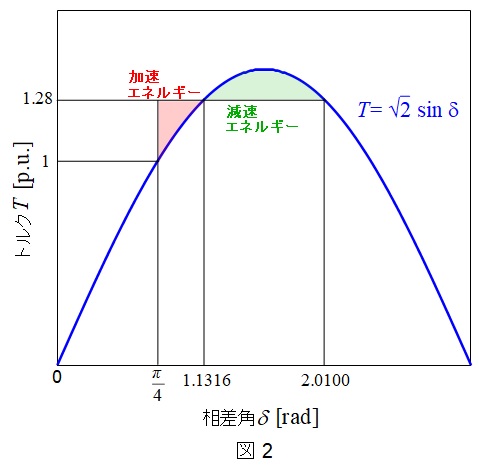
図2において赤塗した箇所が加速エネルギー,緑塗した箇所が最大の減速エネルギーとなるため,緑塗箇所より赤塗箇所の面積の方が大きければ脱調する。それぞれの面積を求めると,加速エネルギー\(W_{1}\)は,
\[
\begin{eqnarray}
W_{1} &=&\int _{\frac {\pi}{4}}^{1.1316} \left( 1.28-\sqrt {2}\sin \delta \right) \mathrm {d}\delta \\[ 5pt ]
&=&\left [ 1.28 \delta +\sqrt {2}\cos \delta \right] _{\frac {\pi}{4}}^{1.1316}\\[ 5pt ]
&=& 1.28 \times \left( 1.1316-\frac {\pi}{4}\right) +\sqrt {2}\left( \cos 1.1316 -\cos \frac {\pi}{4} \right)
\end{eqnarray}
\]
となる。ここで,
\[
\begin{eqnarray}
\cos \ 1.1316 &=&\sqrt {1- \sin ^{2} 1.1316} \\[ 5pt ]
&=&\sqrt {1- 0.90510^{2}} \\[ 5pt ]
&≒&0.42520
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
W_{1} &=&1.28 \times \left( 1.1316-\frac {\pi}{4}\right) +\sqrt {2}\left( \cos 1.1316 -\cos \frac {\pi}{4} \right) \\[ 5pt ]
&≒&1.28 \times \left( 1.1316-0.78540 \right) +\sqrt {2}\left( 0.42520 -\frac {1}{\sqrt {2}} \right) \\[ 5pt ]
&≒& 0.44314 -0.39868 \\[ 5pt ]
&≒& 0.04446
\end{eqnarray}
\]
となる。また,最大減速エネルギー\(W_{2}\)は,
\[
\begin{eqnarray}
W_{2} &=&\int _{1.1316}^{2.0100} \left( \sqrt {2}\sin \delta -1.28\right) d\delta \\[ 5pt ]
&=&\left [ -\sqrt {2}\cos \delta -1.28 \delta \right] _{1.1316}^{2.0100}\\[ 5pt ]
&=&\sqrt {2}\left( -\cos 2.0100 +\cos 1.1316 \right) -1.28 \times \left( 2.0100-1.1316\right) \\[ 5pt ]
&=&\sqrt {2}\left( 0.42520 +0.42520 \right) -1.28 \times \left( 2.0100-1.1316\right) \\[ 5pt ]
&≒&1.20265 -1.12435 \\[ 5pt ]
&≒&0.07830
\end{eqnarray}
\]
となり,\(W_{1} <W_{2}\)となるため,脱調しないことが分かる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん