【問題】
【難易度】★★★★☆(やや難しい)
三相ブリッジ接続のサイリスタ変換装置に関して,次の問に答えよ。
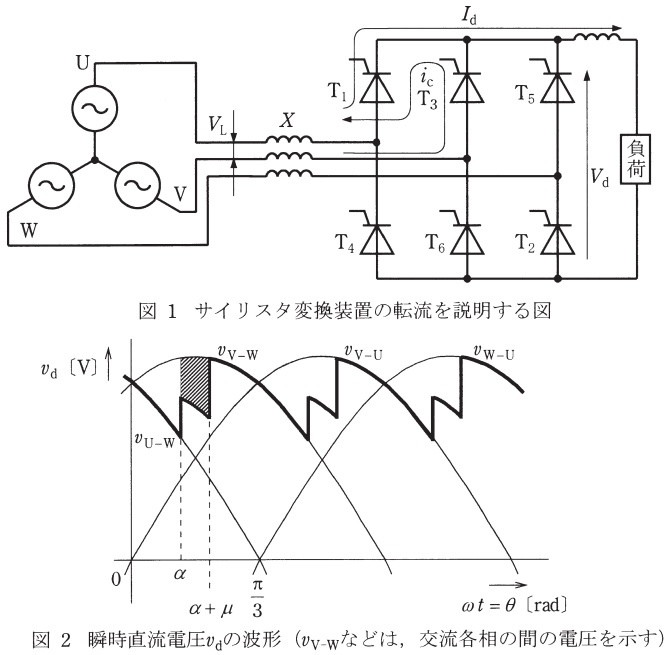
(1) 図1は,三相ブリッジ接続サイリスタ変換装置の転流を説明する図である。変換装置用変圧器の交流(一次)側は,直流(二次)側に換算している。交流電源電圧は\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)で,変換装置用変圧器の短絡リアクタンスは\( \ X \ \mathrm {[\Omega ]} \ \)である。交流回路にはそれ以外にインピーダンスがなく,サイリスタのオン電圧(電圧降下)は無視できる。直流回路にはインダクタンスが十分に大きな直流リアクトルが接続されており,直流電流は一定値\( \ I_{\mathrm {d}} \ \mathrm {[A]} \ \)で脈動が無視できる。
サイリスタ\( \ \mathrm {T}_{1} \ \)が通電しているときに制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)でサイリスタ\( \ \mathrm {T}_{3} \ \)がオンすると,重なり角\( \ \mu \ \mathrm {[rad]} \ \)の期間,図1に示すように転流電流\( \ i_{\mathrm {c}} \ \mathrm {[A]} \ \)が流れる。転流電圧が零のときを基準とした電気角\( \ \omega t =\theta \ \mathrm {[rad]} \ \)が\( \ \alpha \ \mathrm {[rad]} \ \)のときに\( \ i_{\mathrm {c}}=0 \ \mathrm {[A]} \ \)で転流が開始し,\( \ \alpha +\mu \ \mathrm {[rad]} \ \)のときに\( \ i_{\mathrm {c}}=I_{\mathrm {d}} \ \mathrm {[A]} \ \)となって転流が完了する。\( \ \cos \left( \alpha +\mu \right) \ \mathrm {[rad]} \ \)を\( \ V_{\mathrm {L}} \ \),\( \ I_{\mathrm {d}} \ \),\( \ \alpha \ \)及び\( \ X \ \)を用いて表せ。
(2) 瞬時直流電圧\( \ v_{\mathrm {d}} \ \mathrm {[V]} \ \)は,重なり角によって図2に示すハッチング部分が低下するため,制御遅れ角が\( \ \alpha \ \mathrm {[rad]} \ \)のときの直流電圧(平均値)\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は\( \ \displaystyle \frac {3\sqrt {2}}{\pi }V_{\mathrm {L}}\cos \alpha \ \mathrm {[V]} \ \)よりも低くなる。\( \ V_{\mathrm {d}} \ \)を\( \ V_{\mathrm {L}} \ \),\( \ I_{\mathrm {d}} \ \),\( \ \alpha \ \)及び\( \ X \ \)を用いて表せ。
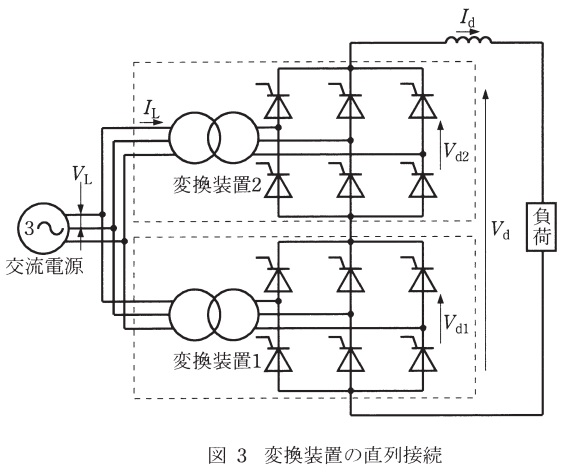
(3) 上記の変換装置\( \ 2 \ \)台を図3に示すように直列に接続した。変換装置用変圧器の交流側(一次)電圧と直流側(二次)電圧との電圧比は\( \ 2 \ \)台とも\( \ 1:1 \ \)であり,交流電源電圧は,\( \ \displaystyle V_{\mathrm {L}}=500\times \frac {\pi }{3\sqrt {2}} \ \mathrm {[V]} \ \)である。直流電流が\( \ I_{\mathrm {d}} \ \mathrm {[A]} \ \)のときのそれぞれの変換装置の交流電流基本波実効値は,\( \ \displaystyle I_{\mathrm {L}}=\frac {\sqrt {6}}{\pi }I_{\mathrm {d}} \ \mathrm {[A]} \ \)で求められるものとする。変換装置\( \ 1 \ \)の直流電圧\( \ V_{\mathrm {d1}} \ \)を\( \ 400 \ \mathrm {[V]} \ \),変換装置\( \ 2 \ \)の直流電圧\( \ V_{\mathrm {d2}} \ \mathrm {[V]} \ \)を\( \ -300 \ \mathrm {[V]} \ \)として,全体で直流電圧\( \ V_{\mathrm {d}}=100 \ \mathrm {[V]} \ \),直流電流\( \ I_{\mathrm {d}}=1000 \ \mathrm {[A]} \ \)を出力した。
a. 交流電源からみたそれぞれの変換装置の入力有効電力\( \ \mathrm {[kW]} \ \)及び基本波無効電力\( \ \mathrm {[kvar]} \ \),並びに,合計の入力有効電力\( \ \mathrm {[kW]} \ \)及び基本波無効電力\( \ \mathrm {[kvar]} \ \)を求めよ。
b. \( \ 2 \ \)台の変換装置全体での交流電源からみた基本波力率\( \ \cos \mathit {\phi }_{1} \ \)を求めよ。
【ワンポイント解説】
パワーエレクトロニクスの問題では一般的に転流を無視する問題が多いですが,今回の問題はその転流部分にフォーカスした問題となっています。比較的計算としては分かりやすい問題なので,1種の問題としては標準的と言えるかもしれません。
【関連する「電気の神髄」記事】
【解答】
(1)\( \ \cos \left( \alpha +\mu \right) \ \mathrm {[rad]} \ \)を\( \ V_{\mathrm {L}} \ \),\( \ I_{\mathrm {d}} \ \),\( \ \alpha \ \)及び\( \ X \ \)を用いて表す
\( \ \alpha < \theta < \alpha +\mu \ \)の時,\( \ i_{\mathrm {c}} \ \)の作る閉回路の回路方程式は,
\[
\begin{eqnarray}
v_{\mathrm {V – U}} &=&2L\frac {\mathrm {d}i_{\mathrm {c}}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
であり,図2より,\( \ v_{\mathrm {V – U}}=\sqrt {2}V_{\mathrm {L}}\sin \theta \ \)であるから,
\[
\begin{eqnarray}
2L\frac {\mathrm {d}i_{\mathrm {c}}}{\mathrm {d}t} &=&\sqrt {2}V_{\mathrm {L}}\sin \theta \\[ 5pt ]
\mathrm {d}i_{\mathrm {c}} &=&\frac {V_{\mathrm {L}}}{\sqrt {2}L}\sin \theta \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \theta =\omega t \ \)すなわち,
\[
\begin{eqnarray}
\frac {\mathrm {d}\theta }{\mathrm {d}t}&=&\omega \\[ 5pt ]
\mathrm {d}\theta &=&\omega \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\mathrm {d}i_{\mathrm {c}} &=&\frac {V_{\mathrm {L}}}{\sqrt {2}L}\sin \theta \mathrm {d}t \\[ 5pt ]
&=&\frac {V_{\mathrm {L}}}{\sqrt {2}\omega L}\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {V_{\mathrm {L}}}{\sqrt {2}X}\sin \theta \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,両辺積分すると,
\[
\begin{eqnarray}
\int _{0}^{I_{\mathrm {d}}}\mathrm {d}i_{\mathrm {c}} &=&\int _{\alpha }^{\alpha +\mu }\frac {V_{\mathrm {L}}}{\sqrt {2}X}\sin \theta \mathrm {d}\theta \\[ 5pt ]
\left[ i_{\mathrm {c}}\right] _{0}^{I_{\mathrm {d}}} &=&\frac {V_{\mathrm {L}}}{\sqrt {2}X}\left[ -\cos \theta \right] _{\alpha }^{\alpha +\mu } \\[ 5pt ]
I_{\mathrm {d}} &=&\frac {V_{\mathrm {L}}}{\sqrt {2}X}\left\{ \cos \alpha -\cos \left( \alpha +\mu \right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \cos \left( \alpha +\mu \right) \ \)について整理すると,
\[
\begin{eqnarray}
\cos \left( \alpha +\mu \right) &=&\cos \alpha -\frac {\sqrt {2}XI_{\mathrm {d}} }{V_{\mathrm {L}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ V_{\mathrm {d}} \ \)を\( \ V_{\mathrm {L}} \ \),\( \ I_{\mathrm {d}} \ \),\( \ \alpha \ \)及び\( \ X \ \)を用いて表す
題意より,転流が無視できる場合の\( \ V_{\mathrm {d}} \ \)は\( \ \displaystyle \frac {3\sqrt {2}}{\pi }V_{\mathrm {L}}\cos \alpha \ \mathrm {[V]} \ \)である。
転流による平均電圧降下\( \ \Delta V_{\mathrm {d}} \ \)は図2のハッチング部分を\( \ \displaystyle \frac {\pi }{3} \ \)で割ったものである。図2より転流時の電圧は,\( \ \displaystyle \frac {v_{\mathrm {V – W}}+v_{\mathrm {U – W}}}{2} \ \)であるから,
\[
\begin{eqnarray}
\Delta V_{\mathrm {d}} &=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\alpha }^{\alpha +\mu } \left( v_{\mathrm {V – W}}-\frac {v_{\mathrm {V – W}}+v_{\mathrm {U – W}}}{2}\right)\mathrm {d}\theta \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\alpha }^{\alpha +\mu } \left( \frac {v_{\mathrm {V – W}}-v_{\mathrm {U – W}}}{2}\right)\mathrm {d}\theta \\[ 5pt ]
&=&\frac {3}{\pi }\int _{\alpha }^{\alpha +\mu } \frac {v_{\mathrm {V – U}}}{2}\mathrm {d}\theta \\[ 5pt ]
&=&\frac {3}{2\pi }\int _{\alpha }^{\alpha +\mu }v_{\mathrm {V – U}}\mathrm {d}\theta \\[ 5pt ]
&=&\frac {3}{2\pi }\int _{\alpha }^{\alpha +\mu }\sqrt {2}V_{\mathrm {L}}\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{\mathrm {L}}}{2\pi }\left[ -\cos \theta\right] _{\alpha }^{\alpha +\mu } \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{\mathrm {L}}}{2\pi }\left\{ \cos \alpha -\cos \left( \alpha +\mu \right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となり,(1)の解答より,
\[
\begin{eqnarray}
\Delta V_{\mathrm {d}} &=&\frac {3\sqrt {2}V_{\mathrm {L}}}{2\pi }\left\{ \cos \alpha -\cos \left( \alpha +\mu \right) \right\} \\[ 5pt ]
&=&\frac {3\sqrt {2}V_{\mathrm {L}}}{2\pi }\cdot \frac {\sqrt {2}XI_{\mathrm {d}} }{V_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {3XI_{\mathrm {d}} }{\pi }\\[ 5pt ]
\end{eqnarray}
\]
となるので,転流を考慮した場合\( \ V_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {d}} &=&\frac {3\sqrt {2}}{\pi }V_{\mathrm {L}}\cos \alpha -\Delta V_{\mathrm {d}} \\[ 5pt ]
&=&\frac {3\sqrt {2}}{\pi }V_{\mathrm {L}}\cos \alpha -\frac {3XI_{\mathrm {d}} }{\pi } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)a.交流電源からみたそれぞれの変換装置の入力有効電力\( \ \mathrm {[kW]} \ \)及び基本波無効電力\( \ \mathrm {[kvar]} \ \),並びに,合計の入力有効電力\( \ \mathrm {[kW]} \ \)及び基本波無効電力\( \ \mathrm {[kvar]} \ \)
変換装置\( \ 1 \ \),\( \ 2 \ \)の入力有効電力\( \ P_{1} \ \),\( \ P_{2} \ \)は,変換装置\( \ 1 \ \),\( \ 2 \ \)からの出力電力と等しいので,
\[
\begin{eqnarray}
P_{1} &=&V_{\mathrm {d1}}I_{\mathrm {d}} \\[ 5pt ]
&=&400\times 1000 \\[ 5pt ]
&=&400000 \ \mathrm {[W]} → 400 \ \mathrm {[kW]} \\[ 5pt ]
P_{2} &=&V_{\mathrm {d2}}I_{\mathrm {d}} \\[ 5pt ]
&=&-300\times 1000 \\[ 5pt ]
&=&-300000 \ \mathrm {[W]} → -300 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,入力皮相電力\( \ S_{1} = S_{2} =S \ \)は,
\[
\begin{eqnarray}
S &=&\sqrt {3}V_{\mathrm {L}}I_{\mathrm {d}} \\[ 5pt ]
&=&\sqrt {3}\times 500\times \frac {\pi }{3\sqrt {2}}\times \frac {\sqrt {6}}{\pi }\times 1000 \\[ 5pt ]
&=&500000 \ \mathrm {[V\cdot A]} → 500 \ \mathrm {[kV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,それぞれの入力無効電力\( \ Q_{1} \ \),\( \ Q_{2} \ \)は,
\[
\begin{eqnarray}
Q_{1} &=&\sqrt {S^{2}-P_{1}^{2}} \\[ 5pt ]
&=&\sqrt {500^{2}-400^{2}} \\[ 5pt ]
&=&300 \ \mathrm {[kvar]} \\[ 5pt ]
Q_{2} &=&\sqrt {S^{2}-P_{2}^{2}} \\[ 5pt ]
&=&\sqrt {500^{2}-\left( -300\right) ^{2}} \\[ 5pt ]
&=&400 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,合計の入力有効電力\( \ P \ \)及び基本波無効電力\( \ Q \ \)は,
\[
\begin{eqnarray}
P &=&P_{1}+P_{2} \\[ 5pt ]
&=&400-300 \\[ 5pt ]
&=&100 \ \mathrm {[kW]} \\[ 5pt ]
Q &=&Q_{1}+Q_{2} \\[ 5pt ]
&=&300+400 \\[ 5pt ]
&=&700 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)b.\( \ 2 \ \)台の変換装置全体での交流電源からみた基本波力率\( \ \cos \mathit {\phi }_{1} \ \)
\( \ 2 \ \)台の変換装置全体での交流電源からみた基本波力率\( \ \cos \mathit {\phi }_{1} \ \)は,
\[
\begin{eqnarray}
\cos \mathit {\phi }_{1} &=&\frac {100}{\sqrt {100^{2}+700^{2}}} \\[ 5pt ]
&=&0.14142 → 0.141 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん