【問題】
【難易度】★★★★☆(やや難しい)
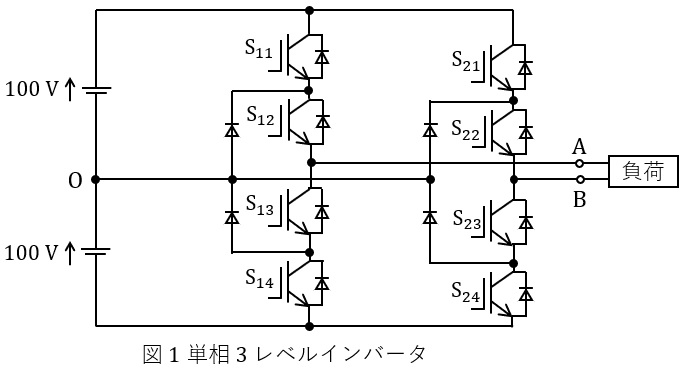
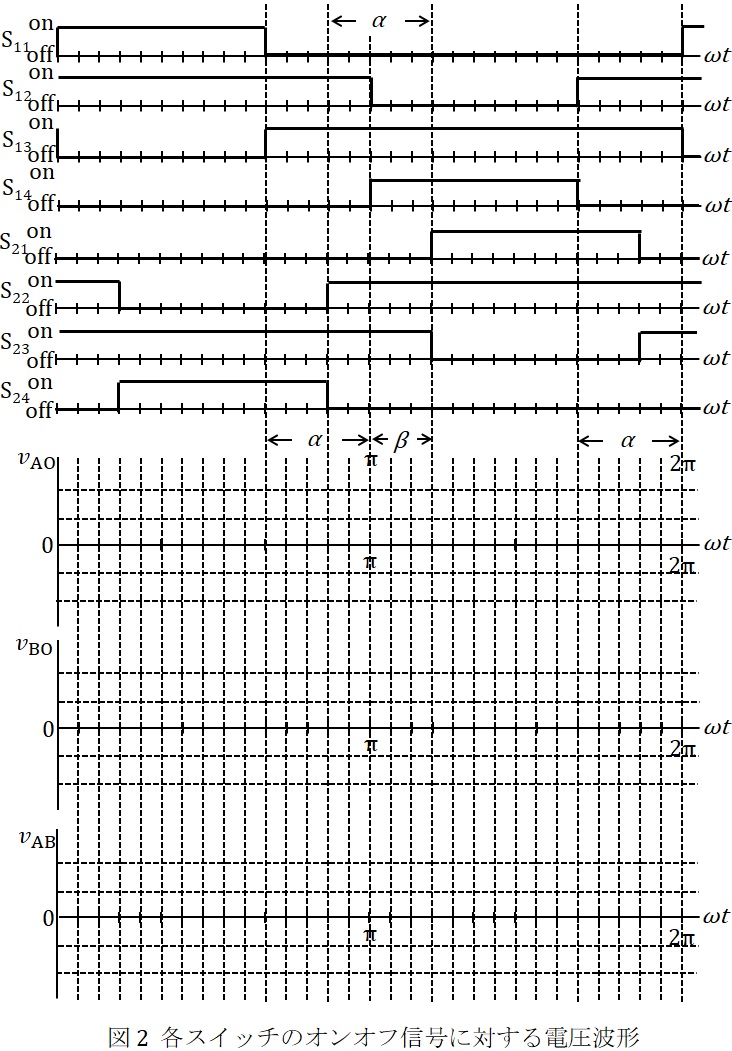
図1に示す単相\( \ 3 \ \)レベルインバータのスイッチ\( \ \mathrm {S_{11}} \ \)~\( \ \mathrm {S_{24}} \ \)を,図2に示すオンオフ信号で動作させた場合について,次の問に答えよ。なお,\( \ \displaystyle \sin \frac {2\pi }{5}=0.951 \ 06 \ \),\( \ \displaystyle \cos \frac {2\pi }{5}=0.309 \ 02 \ \)を必要に応じて用いてよい。
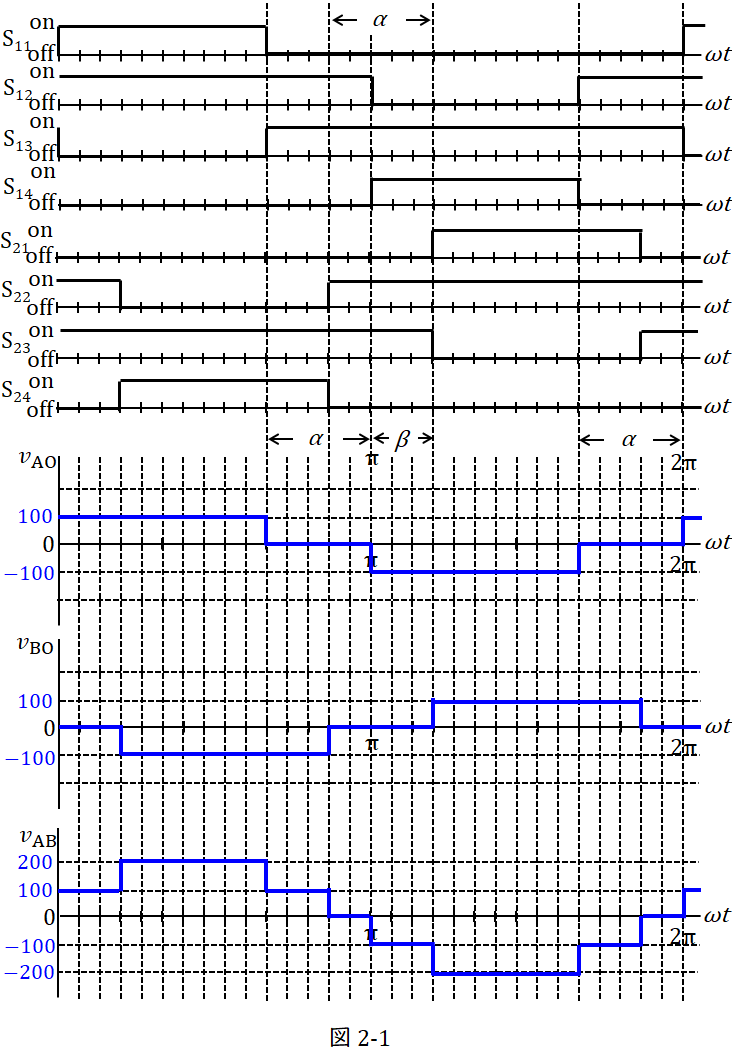
(1) 電源の中性点\( \ \mathrm {O} \ \)を基準としたときの端子\( \ \mathrm {A} \ \)及び端子\( \ \mathrm {B} \ \)の電圧\( \ v_{\mathrm {AO}} \ \),\( \ v_{\mathrm {BO}} \ \),端子\( \ \mathrm {B} \ \)を基準としたときの端子\( \ \mathrm {A} \ \)の電圧(出力電圧)\( \ v_{\mathrm {AB}} \ \)を,それぞれの波形を,波形の大きさとスイッチングの位相が明確に分かるように,答案用紙に印刷されている図2に示せ。
(2) 電圧\( \ v_{\mathrm {AO}} \ \),\( \ v_{\mathrm {BO}} \ \)をフーリエ級数展開した場合,偶数次調波成分は\( \ 0 \ \)になり,奇数\( \ k=\left( 2n-1\right) \ \)次調波成分\( \ \left( n=1,2\cdots \right) \ \)の振幅\( \ V_{k} \ \)は,次式で表される。
\[
\begin{eqnarray}
V_{k} &=&\frac {400}{k\pi }\cos \left( \frac {k\alpha }{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
\( \ \displaystyle \alpha =\frac {\pi }{3} \ \mathrm {rad} \ \)のとき,電圧\( \ v_{\mathrm {AO}} \ \)と\( \ v_{\mathrm {BO}} \ \)のそれぞれについて,基本波成分,第\( \ 3 \ \)次調波成分,第\( \ 5 \ \)次調波成分の実効値を求めよ。
(3) \( \ \displaystyle \alpha =\frac {\pi }{3} \ \mathrm {rad} \ \),\( \ \displaystyle \beta =\frac {\pi }{5} \ \mathrm {rad} \ \)のとき,出力電圧\( \ v_{\mathrm {AB}} \ \)の基本波成分,第\( \ 3 \ \)次調波成分,第\( \ 5 \ \)次調波成分の実効値を求めよ。
【ワンポイント解説】
単相\( \ 3 \ \)レベルインバータの動作と電圧の実効値を求める問題です。
(1)は比較的易しい問題ですが,(2)以降はその場での読解力が必要となり,(3)に関しては図2との対応や位相差の考え方に苦慮する問題であったかと思います。時間がないときの部分点狙いの問題としては良い問題と言えるでしょう。
1.単相\( \ 3 \ \)レベルインバータの動作
本問の単相\( \ 3 \ \)レベルインバータに関して,\( \ \mathrm {S_{11}} \ \)~\( \ \mathrm {S_{14}} \ \)及び\( \ \mathrm {S_{21}} \ \)~\( \ \mathrm {S_{24}} \ \)がそれぞれセットで同じように動作するため,ここでは\( \ \mathrm {S_{11}} \ \)~\( \ \mathrm {S_{14}} \ \)について考えます。取り得るパターンは以下の\( \ 3 \ \)パターンとなります。
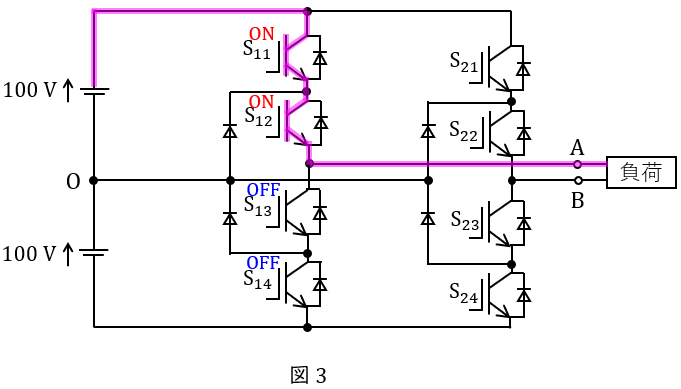
① \( \ \mathrm {S_{11}} \ \)と\( \ \mathrm {S_{12}} \ \)が\( \ \mathrm {ON} \ \),\( \ \mathrm {S_{13}} \ \)と\( \ \mathrm {S_{14}} \ \)が\( \ \mathrm {OFF} \ \)
図3のように導通するため,負荷の端子\( \ \mathrm {A} \ \)は正の電圧\( \ 100 \ \mathrm {V} \ \)が加わり,\( \ v_{\mathrm {AO}}=100 \ \mathrm {[V]} \ \)となります。
② \( \ \mathrm {S_{12}} \ \)と\( \ \mathrm {S_{13}} \ \)が\( \ \mathrm {ON} \ \),\( \ \mathrm {S_{11}} \ \)と\( \ \mathrm {S_{14}} \ \)が\( \ \mathrm {OFF} \ \)
図4のように導通するため,負荷の端子\( \ \mathrm {A} \ \)は\( \ 0 \ \mathrm {V} \ \)となり,\( \ v_{\mathrm {AO}}=0 \ \mathrm {[V]} \ \)となります。

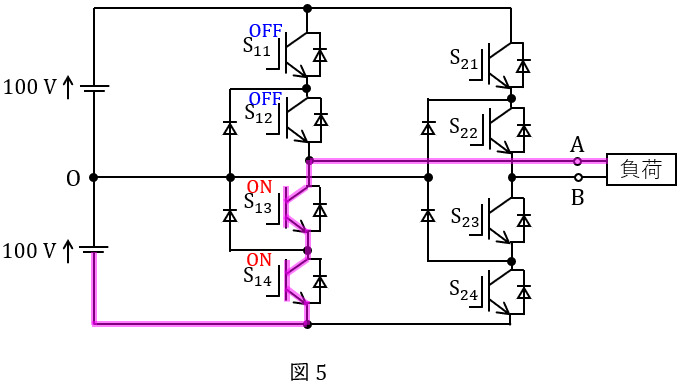
③ \( \ \mathrm {S_{13}} \ \)と\( \ \mathrm {S_{14}} \ \)が\( \ \mathrm {ON} \ \),\( \ \mathrm {S_{11}} \ \)と\( \ \mathrm {S_{12}} \ \)が\( \ \mathrm {OFF} \ \)
図5のように導通するため,負荷の端子\( \ \mathrm {A} \ \)は負の電圧\( \ -100 \ \mathrm {V} \ \)が加わり,\( \ v_{\mathrm {AO}}=-100 \ \mathrm {[V]} \ \)となります。
同様に\( \ \mathrm {S_{21}} \ \)~\( \ \mathrm {S_{24}} \ \)も動作するため,オンオフの組合せにより,線間電圧\( \ v_{\mathrm {AB}} \ \)が\( \ -200 \ \mathrm {V} \ \)から\( \ 200 \ \mathrm {V} \ \)まで,\( \ 100 \ \mathrm {V} \ \)刻みで現れることになります。
【解答】
(1)\( \ v_{\mathrm {AO}} \ \),\( \ v_{\mathrm {BO}} \ \),\( \ v_{\mathrm {AB}} \ \)の波形
ワンポイント解説「1.単相\( \ 3 \ \)レベルインバータの動作」の通り\( \ v_{\mathrm {AO}} \ \),\( \ v_{\mathrm {BO}} \ \)を考え,図の各位相において\( \ v_{\mathrm {AB}}=v_{\mathrm {AO}}-v_{\mathrm {BO}} \ \)を計算すると図2-1のようになる。
(2)\( \ \displaystyle \alpha =\frac {\pi }{3} \ \mathrm {rad} \ \)のとき,電圧\( \ v_{\mathrm {AO}} \ \)と\( \ v_{\mathrm {BO}} \ \)の基本波成分,第\( \ 3 \ \)次調波成分,第\( \ 5 \ \)次調波成分の実効値
与式に\( \ \displaystyle \alpha =\frac {\pi }{3} \ \mathrm {rad} \ \)を代入すると,
\[
\begin{eqnarray}
V_{k} &=&\frac {400}{k\pi }\cos \left( \frac {k\pi }{6}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ k=1,3,5 \ \)を代入すると,各成分の振幅\( \ V_{1} \ \mathrm {[V]} \ \),\( \ V_{3} \ \mathrm {[V]} \ \),\( \ V_{5} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{1} &=&\frac {400}{\pi }\cos \left( \frac {\pi }{6}\right) \\[ 5pt ]
&=&\frac {400}{\pi }\times \frac {\sqrt {3}}{2} \\[ 5pt ]
&≒&110.27 \ \mathrm {[V]} \\[ 5pt ]
V_{3} &=&\frac {400}{3\pi }\cos \left( \frac {3\pi }{6}\right) \\[ 5pt ]
&=&\frac {400}{3\pi }\times 0 \\[ 5pt ]
&=&0 \ \mathrm {[V]} \\[ 5pt ]
V_{5} &=&\frac {400}{5\pi }\cos \left( \frac {5\pi }{6}\right) \\[ 5pt ]
&=&\frac {400}{5\pi }\times \left( -\frac {\sqrt {3}}{2}\right) \\[ 5pt ]
&≒&-22.053 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,それぞれの実効値\( \ V_{\mathrm {AO1}} \ \),\( \ V_{\mathrm {AO3}} \ \),\( \ V_{\mathrm {AO5}} \ \),\( \ V_{\mathrm {BO1}} \ \),\( \ V_{\mathrm {BO3}} \ \),\( \ V_{\mathrm {BO5}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {AO1}}=V_{\mathrm {BO1}} &=&\frac {V_{1}}{\sqrt {2}} \\[ 5pt ]
&=&\frac {110.27}{\sqrt {2}} \\[ 5pt ]
&≒&77.973 → 78.0 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {AO3}}=V_{\mathrm {BO3}} &=&0 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {AO5}}=V_{\mathrm {BO5}} &=&\frac {V_{5}}{\sqrt {2}} \\[ 5pt ]
&=&\frac {22.053}{\sqrt {2}} \\[ 5pt ]
&≒&15.594 → 15.6 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \displaystyle \alpha =\frac {\pi }{3} \ \mathrm {rad} \ \),\( \ \displaystyle \beta =\frac {\pi }{5} \ \mathrm {rad} \ \)のとき,出力電圧\( \ v_{\mathrm {AB}} \ \)の基本波成分,第\( \ 3 \ \)次調波成分,第\( \ 5 \ \)次調波成分の実効値
①基本波成分
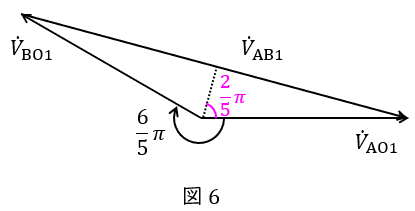
図2-1より,位相は\( \ 15 \ \)マスで\( \ \pi \ \mathrm {rad} \ \)変化しており,\( \ \displaystyle \alpha =\frac {\pi }{3} \ \mathrm {rad} \ \),\( \ \displaystyle \beta =\frac {\pi }{5} \ \mathrm {rad} \ \)のとき,\( \ v_{\mathrm {AO}} \ \)と\( \ v_{\mathrm {BO}} \ \)の基本波の位相差は\( \ 18 \ \)マス分,すなわち\( \ \displaystyle \frac {6}{5}\pi \ \mathrm {rad} \ \)異なることがわかる。
したがって,それぞれの基本波のベクトル図は図6のように描け,\( \ v_{\mathrm {AB}} \ \)の基本波成分実効値\( \ V_{\mathrm {AB1}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {AB1}} &=&2V_{\mathrm {AO1}}\sin \frac {2}{5}\pi \\[ 5pt ]
&=&2\times 77.973\times 0.951 \ 06 \\[ 5pt ]
&≒&148.31 → 148 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
②第\( \ 3 \ \)次調波成分
(2)より,\( \ \displaystyle \alpha =\frac {\pi }{3} \ \mathrm {rad} \ \)のとき,第\( \ 3 \ \)次調波成分の各実効値\( \ V_{\mathrm {AO3}}=V_{\mathrm {BO3}}=0 \ \)となるため,\( \ v_{\mathrm {AB}} \ \)の第\( \ 3 \ \)次調波成分実効値\( \ V_{\mathrm {AB3}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {AB3}} &=&V_{\mathrm {AO3}}-V_{\mathrm {BO3}} \\[ 5pt ]
&=&0 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
③第\( \ 5 \ \)次調波成分
基本波成分が\( \ \displaystyle \frac {6\pi }{5} \ \mathrm {rad} \ \)異なるため,第\( \ 5 \ \)次調波成分の位相差は,
\[
\begin{eqnarray}
\frac {6\pi }{5}\times 5 &=&6\pi \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ V_{\mathrm {AO5}} \ \)と\( \ V_{\mathrm {BO5}} \ \)が同相であることがわかる。よって,\( \ v_{\mathrm {AB}} \ \)の第\( \ 5 \ \)次調波成分実効値\( \ V_{\mathrm {AB5}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {AB5}} &=&V_{\mathrm {AO5}}-V_{\mathrm {BO5}} \\[ 5pt ]
&=&15.594-15.594 \\[ 5pt ]
&=&0 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん