【問題】
【難易度】★★☆☆☆(やや易しい)
三相円筒形同期電動機(星形結線)において,
\( \ \dot E \ \mathrm {[V]} \ \):無負荷誘導起電力(相電圧),
\( \ \dot V \ \mathrm {[V]} \ \):端子電圧(相電圧),
\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \):電機子電流,
\( \ X_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \):同期リアクタンス,
\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \):電機子巻線抵抗,
\( \ \phi \ \mathrm {[rad]} \ \):力率角(遅れ),
\( \ \delta \ \mathrm {[rad]} \ \):負荷角(内部相差角)
とする。また,\( \ \dot E \ \),\( \ \dot V \ \),\( \ {\dot I}_{\mathrm {a}} \ \)の実効値を\( \ E \ \),\( \ V \ \),\( \ I_{\mathrm {a}} \ \)とし,同期インピーダンスを\( \ Z_{\mathrm {s}}=\sqrt {{X_{\mathrm {s}}}^{2}+{R_{\mathrm {a}}}^{2}} \ \mathrm {[\Omega ]} \ \),その角を\( \ \displaystyle \alpha =\tan ^{-1} \left( \frac {X_{\mathrm {s}}}{R_{\mathrm {a}}} \right) \ \mathrm {[rad]} \ \)とする。ただし,鉄損,漂遊負荷損,機械損は無視する。
(1) 機械的出力\( \ P_{\mathrm {out1}} \ \mathrm {[W]} \ \)を\( \ E \ \),\( \ V \ \),\( \ X_{\mathrm {s}} \ \),\( \ \delta \ \)を用いて示せ。ただし,電機子巻線抵抗\( \ R_{\mathrm {a}} \ \)は無視する。
(2) 電動機の出力軸をある負荷に接続し,\( \ V=V_{0} \ \)で運転したとき,負荷角は\( \ \displaystyle \delta _{0} =\frac {\pi }{6} \ \mathrm {rad} \ \)であった。周波数を一定のまま,\( \ V \ \)を徐々に低下すると,\( \ V \lt V_{1} \ \)で脱調した。このときの\( \ V_{1} \ \)を示せ。ただし,励磁電流は一定とし,電機子巻線抵抗\( \ R_{\mathrm {a}} \ \)を無視する。
(3) 電機子巻線抵抗\( \ R_{\mathrm {a}} \ \)を考慮した場合に,この電動機を遅れ力率で運転しているときのフェーザ図を描いて,図中に\( \ \dot E \ \),\( \ \dot V \ \),\( \ {\dot I}_{\mathrm {a}} \ \),\( \ \mathrm {j}X_{\mathrm {s}}{\dot I}_{\mathrm {a}} \ \),\( \ R_{\mathrm {a}}{\dot I}_{\mathrm {a}} \ \),\( \ \phi \ \),\( \ \delta \ \)を示せ。
(4) 電機子巻線抵抗\( \ R_{\mathrm {a}} \ \)を考慮した場合に,電動機の機械的出力\( \ P_{\mathrm {out2}} \ \mathrm {[W]} \ \)を\( \ E \ \),\( \ V \ \),\( \ \delta \ \),\( \ Z_{\mathrm {s}} \ \),\( \ \alpha \ \)を用いて示せ。
(5) 小問(4)において,機械的出力\( \ P_{\mathrm {out2}} \ \)を最大とする\( \ \delta \ \)を示すとともに,その際の\( \ P_{\mathrm {out2}} \ \)を示せ。
【ワンポイント解説】
電機子巻線抵抗を考慮した三相円筒形同期電動機に関する問題です。
(4)の計算が幾分面倒ですが,\( \ 1 \ \)種の問題の計算量としては標準的かと思います。
ぜひ高い計算力を身につけて完答を目指すようにして下さい。
1.同期電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
同期電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ]
&=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ]
&=&\frac {4\pi f}{p} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.三相同期電動機の等価回路及びベクトル図
三相同期電動機の等価回路は,端子電圧\( \ \dot V \ \mathrm {[V]} \ \)(相電圧),誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)(相電圧),電機子電流\( \ \dot I \ \mathrm {[A]} \ \),同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)とすると,図1のようになります。ただし,電機子巻線抵抗は十分に小さいものとします。
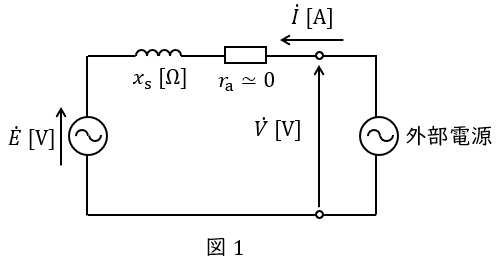
等価回路にキルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
\dot V &=& \dot E+\mathrm {j}x_{\mathrm {s}}\dot I \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
これより,\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot I \ \mathrm {[A]} \ \)の力率角を\( \ \theta \ \mathrm {[rad]} \ \),\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot E \ \mathrm {[V]} \ \)の負荷角を\( \ \delta \ \mathrm {[rad]} \ \)とすると,ベクトル図は図2のように描くことができます。
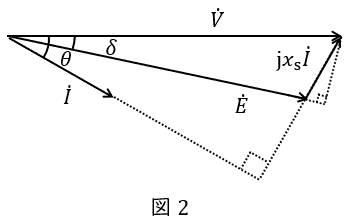
3.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)
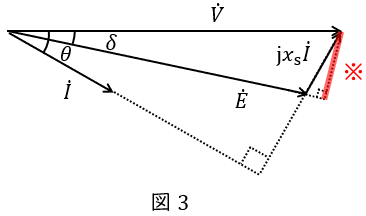
図3のベクトル図に示すように,端子電圧\( \ \dot V \ \mathrm {[V]} \ \)(相電圧),誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)(相電圧),電機子電流\( \ \dot I \ \mathrm {[A]} \ \),\( \ \dot E \ \)と\( \ \dot V \ \)の位相差(負荷角)を\( \ \delta \ \mathrm {[rad]} \ \),\( \ \dot V \ \)と\( \ \dot I \ \)の位相差(力率角)を\( \ \theta \ \mathrm {[rad]} \ \)とすると,出力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&3EI\cos \left( \theta -\delta \right) \\[ 5pt ]
\end{eqnarray}
\]
で求められ,図3の※線を求める式より,
\[
\begin{eqnarray}
x_{\mathrm {s}}I\cos \left( \theta -\delta \right) &=&V\sin \delta \\[ 5pt ]
I\cos \left( \theta -\delta \right) &=&\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
P &=&3EI\cos \left( \theta -\delta \right) \\[ 5pt ]
&=&3E\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ]
&=&\frac {3VE}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
と求められます。最後の式は公式として覚えておくと良いでしょう。
4.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係
同期電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係は,同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)とすると,
\[
\begin{eqnarray}
P &=&\omega _{\mathrm {s}} T \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)機械的出力\( \ P_{\mathrm {out1}} \ \mathrm {[W]} \ \)
ワンポイント解説「3.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)」の通り,機械的出力\( \ P_{\mathrm {out1}} \ \mathrm {[W]} \ \)を\( \ E \ \),\( \ V \ \),\( \ X_{\mathrm {s}} \ \),\( \ \delta \ \)を用いて表すと,
\[
\begin{eqnarray}
P_{\mathrm {out1}} &=&\frac {3VE}{X_{\mathrm {s}}}\sin \delta \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)同期電動機が脱調するときの\( \ V_{1} \ \)
(1)解答式の両辺を\( \ \delta \ \)で微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}P_{\mathrm {out1}}}{\mathrm {d}\delta } &=&\frac {3VE}{X_{\mathrm {s}}}\cos \delta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}P_{\mathrm {out1}}}{\mathrm {d}\delta } \lt 0 \ \)のとき,すなわち\( \ \displaystyle \delta \gt \frac {\pi }{2} \ \)となるとき脱調する。よって,\( \ V=V_{1} \ \)のとき\( \ \displaystyle \delta = \frac {\pi }{2} \ \)であることがわかる。電動機の角速度を\( \ \omega \ \mathrm {[rad]} \ \)とすると,このときのトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,ワンポイント解説「4.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係」の通り,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {out1}}}{\omega } \\[ 5pt ]
&=&\frac {3V_{1}E}{\omega X_{\mathrm {s}}}\sin \frac {\pi }{2} \\[ 5pt ]
&=&\frac {3V_{1}E}{\omega X_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,\( \ V=V_{0} \ \),\( \ \displaystyle \delta _{0} =\frac {\pi }{6} \ \mathrm {[rad]} \ \)のとき,角速度を\( \ \omega \ \mathrm {[rad]} \ \)とすると,負荷トルク\( \ T_{\mathrm {L}} \ \mathrm {[N\cdot m]} \ \)は,ワンポイント解説「4.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係」の通り,
\[
\begin{eqnarray}
T_{\mathrm {L}} &=&\frac {P_{\mathrm {out1}}}{\omega } \\[ 5pt ]
&=&\frac {3V_{0}E}{\omega X_{\mathrm {s}}}\sin \frac {\pi }{6} \\[ 5pt ]
&=&\frac {3V_{0}E}{2\omega X_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ T=T_{\mathrm {L}} \ \)から,
\[
\begin{eqnarray}
\frac {3V_{1}E}{\omega X_{\mathrm {s}}} &=&\frac {3V_{0}E}{2\omega X_{\mathrm {s}}} \\[ 5pt ]
V_{1}&=&\frac {V_{0}}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)電機子巻線抵抗\( \ R_{\mathrm {a}} \ \)を考慮した場合の遅れ力率で運転しているときのフェーザ図
電機子巻線抵抗\( \ R_{\mathrm {a}} \ \)を考慮した場合のフェーザ図は図4のようになる。
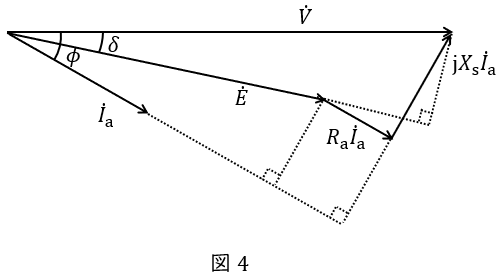
(4)電機子巻線抵抗\( \ R_{\mathrm {a}} \ \)を考慮した場合の電動機の機械的出力\( \ P_{\mathrm {out2}} \ \mathrm {[W]} \ \)
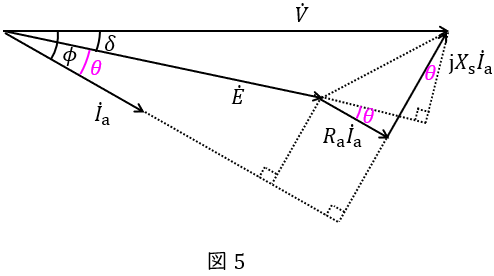
\( \ \theta =\phi -\delta \ \)とするとフェーザ図は図5のようになる。フェーザ図より,
\[
\begin{eqnarray}
V\sin \delta &=&X_{\mathrm {s}}I_{\mathrm {a}}\cos \theta -R_{\mathrm {a}}I_{\mathrm {a}}\sin \theta & ・・・・・・・・・・ ①& \\[ 5pt ]
V\cos \delta &=&E+R_{\mathrm {a}}I_{\mathrm {a}}\cos \theta +X_{\mathrm {s}}I_{\mathrm {a}}\sin \theta & ・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ①\times X_{\mathrm {s}}+②\times R_{\mathrm {a}} \ \)により\( \ \sin \theta \ \)を消去すると,
\[
\begin{eqnarray}
VX_{\mathrm {s}}\sin \delta +VR_{\mathrm {a}}\cos \delta &=&ER_{\mathrm {a}}+{R_{\mathrm {a}}}^{2}I_{\mathrm {a}}\cos \theta +{X_{\mathrm {s}}}^{2}I_{\mathrm {a}}\cos \theta \\[ 5pt ]
VR_{\mathrm {a}}\cos \delta +VX_{\mathrm {s}}\sin \delta -ER_{\mathrm {a}}&=&\left( {R_{\mathrm {a}}}^{2} +{X_{\mathrm {s}}}^{2}\right) I_{\mathrm {a}}\cos \theta \\[ 5pt ]
I_{\mathrm {a}}\cos \theta &=&\frac {VR_{\mathrm {a}}\cos \delta +VX_{\mathrm {s}}\sin \delta -ER_{\mathrm {a}}}{{R_{\mathrm {a}}}^{2} +{X_{\mathrm {s}}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,電動機の機械的出力\( \ P_{\mathrm {out2}} \ \mathrm {[W]} \ \)は,ワンポイント解説「3.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)」の通り,
\[
\begin{eqnarray}
P_{\mathrm {out2}} &=&3EI_{\mathrm {a}}\cos \theta \\[ 5pt ]
&=&3E\cdot \frac {VR_{\mathrm {a}}\cos \delta +VX_{\mathrm {s}}\sin \delta -ER_{\mathrm {a}}}{{R_{\mathrm {a}}}^{2} +{X_{\mathrm {s}}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ R_{\mathrm {a}}=Z_{\mathrm {s}}\cos \alpha \ \),\( \ X_{\mathrm {s}}=Z_{\mathrm {s}}\sin \alpha \ \),\( \ Z_{\mathrm {s}}=\sqrt {{R_{\mathrm {a}}}^{2} +{X_{\mathrm {s}}}^{2}} \ \)より,
\[
\begin{eqnarray}
P_{\mathrm {out2}} &=&3E\cdot \frac {VZ_{\mathrm {s}}\cos \alpha \cos \delta +VZ_{\mathrm {s}}\sin \alpha \sin \delta -EZ_{\mathrm {s}}\cos \alpha }{{Z_{\mathrm {s}}}^{2} } \\[ 5pt ]
&=&3E\cdot \frac {V\cos \alpha \cos \delta +V\sin \alpha \sin \delta -E\cos \alpha }{Z_{\mathrm {s}} } \\[ 5pt ]
&=&\frac {3E}{{Z_{\mathrm {s}} }}\left( V\cos \alpha \cos \delta +V\sin \alpha \sin \delta -E\cos \alpha \right) \\[ 5pt ]
&=&\frac {3E}{{Z_{\mathrm {s}} }}\left\{ V\cos \left( \alpha -\delta \right) -E\cos \alpha \right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)機械的出力\( \ P_{\mathrm {out2}} \ \)を最大とする\( \ \delta \ \)とその際の\( \ P_{\mathrm {out2}} \ \)
(4)解答式の両辺を\( \ \delta \ \)で微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}P_{\mathrm {out2}}}{\mathrm {d} \delta } &=&\frac {3E}{{Z_{\mathrm {s}} }}V\sin \left( \alpha -\delta \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ P_{\mathrm {out2}} \ \)が最大となるとき,\( \ \displaystyle \frac {\mathrm {d}P_{\mathrm {out2}}}{\mathrm {d} \delta }=0 \ \)であるから,
\[
\begin{eqnarray}
\frac {3E}{{Z_{\mathrm {s}} }}V\sin \left( \alpha -\delta \right) &=&0 \\[ 5pt ]
\sin \left( \alpha -\delta \right) &=&0 \\[ 5pt ]
\alpha -\delta &=&0 \\[ 5pt ]
\delta &=&\alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,このときの\( \ P_{\mathrm {out2}} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {out2}}&=&\frac {3E}{{Z_{\mathrm {s}} }}\left\{ V\cos \left( \alpha -\alpha \right) -E\cos \alpha \right\} \\[ 5pt ]
&=&\frac {3E}{{Z_{\mathrm {s}} }}\left( V -E\cos \alpha \right) \\[ 5pt ]
&=&\frac {3VE}{{Z_{\mathrm {s}} }}\left( 1 -\frac {E}{V}\cos \alpha \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。





















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん