【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,直流回路の消費電力に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
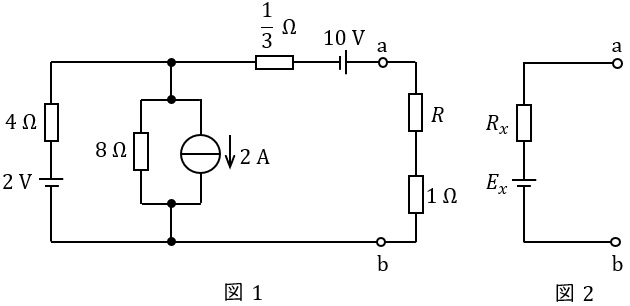
図1に示す回路において,抵抗\( \ R \ \)で消費される電力が最大になる条件とそのときに\( \ R \ \)で消費される電力を求めたい。
図1の回路の端子\( \ \mathrm {a-b} \ \)より左側の部分を図2に示す単一の抵抗\( \ R_{x} \ \)と単一の電圧源\( \ E_{x} \ \)からなる等価回路に変換する。このとき,\( \ R_{x}= \ \fbox { (1) } \ \mathrm {[\Omega ]} \ \),\( \ E_{x}= \ \fbox { (2) } \ \mathrm {[V]} \ \)となる。
次に,抵抗\( \ R \ \)と\( \ 1 \ \mathrm {[\Omega ]} \ \)の抵抗の直列回路を図2の端子\( \ \mathrm {a-b} \ \)間に接続した場合を考えれば,抵抗\( \ R \ \)で消費される電力\( \ P \ \)は\( \ \fbox { (3) } \ \mathrm {[W]} \ \)となり,これより\( \ P \ \)の最大値は\( \ \fbox { (4) } \ \mathrm {[W]} \ \),また,このときの\( \ R \ \)は\( \ \fbox { (5) } \ \mathrm {[\Omega ]} \ \)となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& 1 &(ロ)& \frac {25R}{\left( R+3\right) ^{2}} &(ハ)& 2.9 \\[ 5pt ]
&(ニ)& 4 &(ホ)& 1.8 &(ヘ)& 2.25 \\[ 5pt ]
&(ト)& 7 &(チ)& 8 &(リ)& \frac {16R}{\left( R+5\right) ^{2}} \\[ 5pt ]
&(ヌ)& \frac {36R}{\left( R+4\right) ^{2}} &(ル)& 4.5 &(ヲ)& 6 \\[ 5pt ]
&(ワ)& 2 &(カ)& 3 &(ヨ)& 5 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
直流回路の最大消費電力を求める問題です。
等価変換を用いずにキルヒホッフの法則とテブナンの定理を駆使して解くことも可能かと思いますが,本問の場合は等価変換を用いると最も効率的に解けるかと思います。
電圧源と電流源が組み合わされた問題は等価変換を用いることが可能かどうかをまず検討すると良いでしょう。
1.テブナンの定理
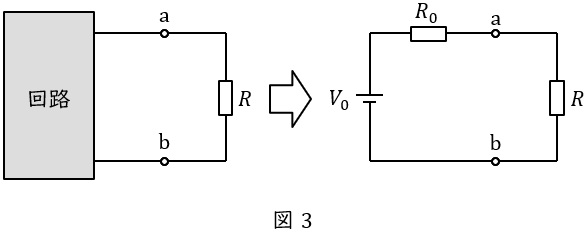
図3のように複雑な回路を電圧源\( \ V_{0} \ \mathrm {[V]} \ \)と抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)に置き換える方法です。
\( \ V_{0} \ \mathrm {[V]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)の開放電圧,\( \ R_{0} \ \mathrm {[\Omega ]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)から電源側回路を見た合成抵抗となります。
ただし,\( \ R_{0} \ \mathrm {[\Omega ]} \ \)を求める際,電圧源は短絡,電流源は開放します。
2.電圧源と電流源の等価変換
図4に示すように,電圧源と電流源は抵抗との直列接続と並列接続で等価変換をすることができます。
電圧源の電圧\( \ E \ \mathrm {[V]} \ \)と電流源の電流\( \ I \ \mathrm {[A]} \ \)には,
\[
\begin{eqnarray}
E &=&rI \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。

【解答】
(1)解答:カ
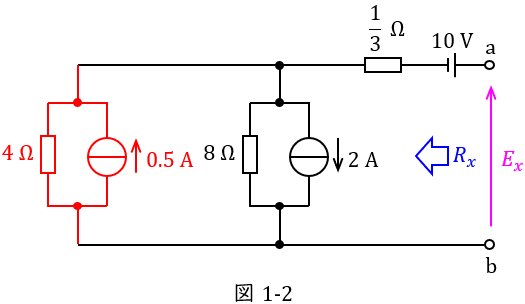
ワンポイント解説「1.テブナンの定理」の通り,求める図2の\( \ R_{x} \ \)と\( \ E_{x} \ \)は図1-1に示す値である。

ワンポイント解説「2.電圧源と電流源の等価変換」の通り,図1-1の\( \ 2 \ \mathrm {V} \ \)の電圧源と\( \ 4 \ \mathrm {\Omega } \ \)の抵抗を等価変換すると図1-2の通りとなる。ただし,電流源の大きさは\( \ \displaystyle \frac {2}{4}=0.5 \ \mathrm {[A]} \ \)(上向き)である。
次に,図1-2の電流源を一つにまとめ,合成抵抗を求めると図1-3の通りとなる。ただし,電流源の大きさは\( \ \displaystyle 2-0.5=1.5 \ \mathrm {[A]} \ \)(下向き),合成抵抗の大きさは\( \ \displaystyle \frac {8\times 4}{8+4}≒2.667 \ \mathrm {[\Omega ]} \ \)である。
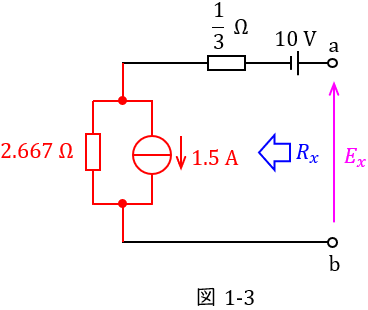
さらに,ワンポイント解説「2.電圧源と電流源の等価変換」の通り,図1-3の\( \ 1.5 \ \mathrm {[A]} \ \)の電流源と\( \ 2.667 \ \mathrm {\Omega } \ \)の抵抗を等価変換すると図1-4の通りとなる。ただし,電圧源の大きさは,\( \ \displaystyle 2.667\times 1.5≒4.00 \ \mathrm {[V]} \ \)である。
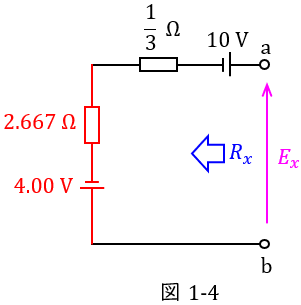
最後に,図1-4の電圧源と抵抗を一つにまとめると図1-5の通りとなる。ただし,電圧源の大きさは\( \ 10-4.00=6.00 \ \mathrm {[V]} \ \),\( \ \displaystyle 2.667+\frac {1}{3}≒3.00 \ \mathrm {[\Omega ]} \ \)である。
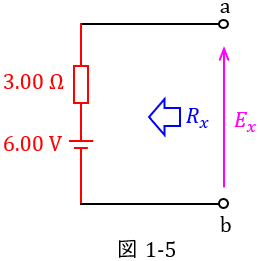
以上から,\( \ R_{x}=3 \ \mathrm {[\Omega ]} \ \)と求められる。
(2)解答:ヲ
図1-5より,\( \ E_{x}= 6 \ \mathrm {[V]} \ \)と求められる。
(3)解答:ヌ
(1)及び(2)より,図1の回路は図1-6のように書き換えることができる。このとき回路を流れる電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=&\frac {6.00}{3.00+R+1} \\[ 5pt ]
&=&\frac {6}{R+4} \\[ 5pt ]
\end{eqnarray}
\]
となるので,抵抗\( \ R \ \)で消費される電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ]
&=&R\left( \frac {6}{R+4}\right) ^{2} \\[ 5pt ]
&=&\frac {36R}{\left( R+4\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
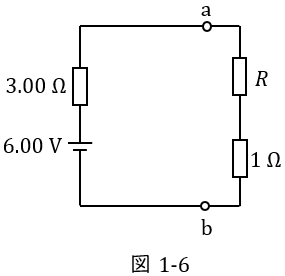
(4)解答:ヘ
(3)解答式を変形すると,
\[
\begin{eqnarray}
P &=&\frac {36R}{\left( R+4\right) ^{2}} \\[ 5pt ]
&=&\frac {36R}{R^{2}+8R+16} \\[ 5pt ]
&=&\frac {36}{\displaystyle R+8+\frac {16}{R}} \\[ 5pt ]
\end{eqnarray}
\]
となり,上式の分母が最小値となるとき\( \ P \ \)が最大値となることがわかる。よって,\( \ A=\displaystyle R+8+\frac {16}{R} \ \)と置けば,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}R} =1-\frac {16}{R^{2}}&=&0 \\[ 5pt ]
1&=&\frac {16}{R^{2}} \\[ 5pt ]
R^{2}&=&16 \\[ 5pt ]
R&=&4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
のとき,消費電力は最大値となる。よって,\( \ P \ \)の最大値\( \ P_{\mathrm {m}} \ \mathrm {[W]} \ \)は,(3)解答式に\( \ R=4 \ \mathrm {[\Omega ]} \ \)を代入すれば,
\[
\begin{eqnarray}
P_{\mathrm {m}} &=&\frac {36R}{\left( R+4\right) ^{2}} \\[ 5pt ]
&=&\frac {36\times 4}{\left( 4+4\right) ^{2}} \\[ 5pt ]
&=&2.25 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※ もちろん,\( \ 3 \ \)種で学習する最小定理で\( \ R=4 \ \mathrm {[\Omega ]} \ \)と求めても大丈夫です。
(5)解答:ニ
(4)より,\( \ R=4 \ \mathrm {[\Omega ]} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん