《理論》〈電気回路〉[H29:問6] 2端子対抵抗回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

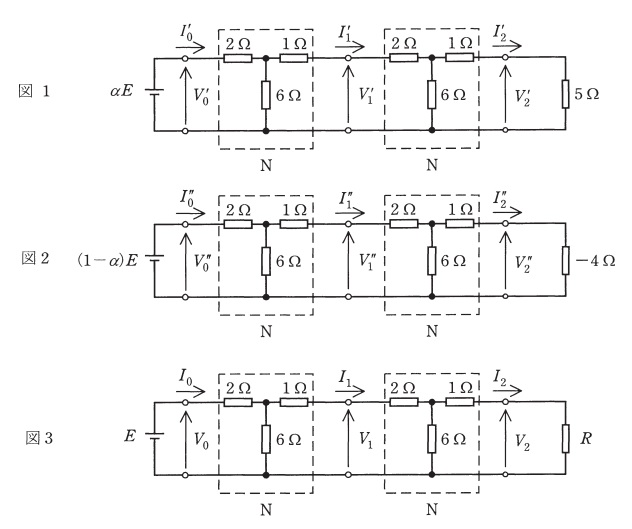
次の文章は，直流電源と$ \ 2 \ $端子対抵抗回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

図のように，$ \ 3 \ $種類の直流電圧源$ \ \alpha E \ $，$ \ (1-\alpha )E \ $，$ \ E \ $に同一の$ \ 2 \ $端子対回路$ \ N \ $を$ \ 2 \ $段接続し，それぞれ異なる抵抗で終端した。図1，図2の回路では，
\[
\frac {V^{\prime}_{0}}{I^{\prime}_{0}}=\frac {V^{\prime}_{1}}{I^{\prime}_{1}}=\frac {V^{\prime}_{2}}{I^{\prime}_{2}}=5 \ \Omega，　\frac {V^{\prime\prime}_{0}}{I^{\prime\prime}_{0}}=\frac {V^{\prime\prime}_{1}}{I^{\prime\prime}_{1}}=\frac {V^{\prime\prime}_{2}}{I^{\prime\prime}_{2}}=-4 \ \Omega　\ ・・・・・・・①
\] が成立する。更に，分圧比，分流比の計算から，定数$ \ \lambda \ $を用いて，①式の電圧，電流は，以下の等比数列で表すことができる。
\[
V^{\prime}_{k}=\lambda ^{-k}\alpha E，I^{\prime}_{k}=\lambda ^{-k}\frac {\alpha E}{5}，k=0，1，2　・・・・・・・・・・・・・・②
\] \[
V^{\prime\prime}_{k}=\lambda ^{k}(1-\alpha )E，I^{\prime\prime}_{k}=-\lambda ^{k}\frac {(1-\alpha )E}{4}，k=0，1，2　・・・・・・・・③
\] ここで，$ \ \lambda =\fbox {　（１）　} \ $であり，$ \ \lambda \ $とその逆数$ \ \lambda ^{-1} \ $は，図の$ \ 2 \ $端子対回路$ \ \mathrm {N} \ $の$ \ \fbox {　（２）　} \ $の固有値である。
次に，図3の回路を解析する。任意の抵抗$ \ R \ $に対し，図3の電圧$ \ V_{k} \ $は図1の電圧$ \ V^{\prime}_{k} \ $と図2の電圧$ \ V^{\prime\prime}_{k} \ $の和で，図3の電流$ \ I_{k} \ $は図1の電流$ \ I^{\prime }_{k} \ $と図2の電流$ \ I^{\prime\prime}_{k} \ $の和で，それぞれ表すことができる。
\[
V_{k}=V^{\prime}_{k}+V^{\prime\prime}_{k}，I_{k}=I^{\prime }_{k}+I^{\prime\prime}_{k}，k=0，1，2　・・・・・・・・・・・・・・④
\] ただし，$ \ \alpha \ $は，図3の終端で④式の$ \ V_{2} \ $と$ \ I_{2} \ $が$ \ \fbox {　（３）　} \ $の法則を満たす定数であり，$ \ \displaystyle \frac {V_{2}}{I_{2}}=\frac {V^{\prime}_{2}+V^{\prime\prime}_{2}}{I^{\prime }_{2}+I^{\prime\prime}_{2}}=R \ $の式から一意に決定できる。例えば，$ \ R=0 \ \Omega \ $(短絡)のときは，④式で$ \ V_{2}=V^{\prime}_{2}+V^{\prime\prime}_{2}=0 \ $となる。この式に$ \ \lambda =\fbox {　（１）　} \ $と，$ \ k=2 \ $のときの②式及び③式を代入すると，$ \ \alpha =\fbox {　（４）　} \ $を得る。これにより電流$ \ I_{0} \ $は，$ \ I_{0}=I^{\prime }_{0}+I^{\prime\prime}_{0}=\fbox {　（５）　} \ [\mathrm {A}] \ $となる。
なお，以上の解析法は，回路の段数が$ \ 3 \ $段以上の場合にも適用できる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {15}{13}　　　&（ロ）&　オーム　　　&（ハ）&　3 \\[ 5pt ] &（ニ）&　\mathrm {Z}行列　　　&（ホ）&　\frac {23}{100}E　　　&（ヘ）&　ジュール \\[ 5pt ] &（ト）&　4　　　&（チ）&　アンペール　　　　&（リ）&　\frac {16}{15} \\[ 5pt ] &（ヌ）&　-\frac {13}{16}　　　&（ル）&　\mathrm {F}行列　　　&（ヲ）&　\frac {19}{100}E \\[ 5pt ] &（ワ）&　\frac {21}{100}E　　　&（カ）&　\mathrm {S}行列　　　&（ヨ）&　2
\end{eqnarray}
\]

【ワンポイント解説】

近年出題が見られないような問題です。問題文をきちんと読解すれば，(1)，(4)，(5)は回路計算で解決できます。$\mathrm {Z}$行列と$\mathrm {F}$行列の定義を本問で理解しておきましょう。

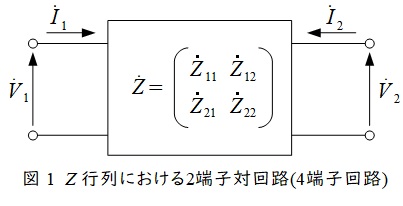
1.$ \ \mathrm {Z}$行列と$ \ \mathrm {F}$行列
$ \ 2 \ $端子対回路は以下のように定義されます。
a.$ \ \mathrm {Z} \ $行列
図1の回路において$ \ \mathrm {Z} \ $行列は，
\[
\begin{bmatrix} \dot V_{1} \\ \dot V_{2} \end{bmatrix}=\begin{bmatrix} {\dot Z}_{11} & {\dot Z}_{12} \\ {\dot Z}_{21} & {\dot Z}_{22} \end{bmatrix}\begin{bmatrix} \dot I_{1} \\ \dot I_{2} \end{bmatrix}
\] となり，各$ \ \mathrm {Z} \ $パラメータは，
\[
\begin{eqnarray}
{\dot Z}_{11} = {{\dot V}_{1} \abovewithdelims . | 0.5pt {\dot I}_{1}}_{{\dot I}_{2}=0} \\[ 5pt ] {\dot Z}_{12} = {{\dot V}_{1} \abovewithdelims . | 0.5pt {\dot I}_{2}}_{{\dot I}_{1}=0} \\[ 5pt ] {\dot Z}_{21} = {{\dot V}_{2} \abovewithdelims . | 0.5pt {\dot I}_{1}}_{{\dot I}_{2}=0} \\[ 5pt ] {\dot Z}_{22} = {{\dot V}_{2} \abovewithdelims . | 0.5pt {\dot I}_{2}}_{{\dot I}_{1}=0}
\end{eqnarray}
\] で求められます。

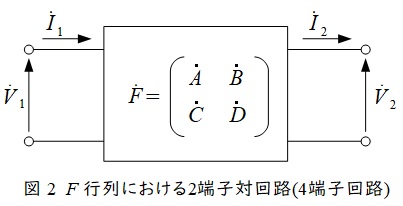
b.$ \ \mathrm {F} \ $行列
図2の回路において($ \ {\dot I}_{2} \ $の電流の向きに注意して下さい。)，$ \ \mathrm {F} \ $行列は，
\[
\begin{bmatrix} {\dot V}_{1} \\ {\dot I}_{1} \end{bmatrix}=\begin{bmatrix} \dot A & \dot B \\ \dot C & \dot D \end{bmatrix}\begin{bmatrix} {\dot V}_{2} \\ {\dot I}_{2} \end{bmatrix}
\] となり，各$ \ \mathrm {F} \ $パラメータは，
\[
\begin{eqnarray}
\dot A = {{\dot V}_{1} \abovewithdelims . | 0.5pt {\dot V}_{2}}_{{\dot I}_{2}=0} \\[ 5pt ] \dot B = {{\dot V}_{1} \abovewithdelims . | 0.5pt {\dot I}_{2}}_{{\dot V}_{2}=0} \\[ 5pt ] \dot C = {{\dot I}_{1} \abovewithdelims . | 0.5pt {\dot V}_{2}}_{{\dot I}_{2}=0} \\[ 5pt ] \dot D = {{\dot I}_{1} \abovewithdelims . | 0.5pt {\dot I}_{2}}_{{\dot V}_{2}=0}
\end{eqnarray}
\] で求められます。

2.$ \ \mathrm {F} \ $行列の固有値
$ \ \mathrm {F} \ $行列の固有値$ \ \lambda \ $は，$ \ \mathrm{ det }\left( \dot F-\lambda \dot E\right) =0 \ $で求められます。すなわち，
\[
\begin{eqnarray}
\mathrm{ det }\left( \dot F-\lambda \dot E\right) &=& 0 \\[ 5pt ] \mathrm{ det } \begin{pmatrix} A-\lambda & B \\ C & D-\lambda \end{pmatrix}&=& 0 \\[ 5pt ] (A-\lambda)(D-\lambda)-BC &=& 0
\end{eqnarray}
\] で求められる$ \ \lambda \ $が固有値となります。

【解答】

(1)解答：ヨ
図1の回路において，$ \ {V_{0}}^{\prime } \ $から右側，$ \ {V_{1}}^{\prime } \ $から右側の合成抵抗が$ \ 5 \ \Omega \ $であるから，
\[
{I_{0}}^{\prime }=2{I_{1}}^{\prime }=4{I_{2}}^{\prime }　・・・⑤
\] となる。また，$ \ {V_{1}}^{\prime } \ $は，
\[
{V_{1}}^{\prime }={V_{0}}^{\prime }-2{I_{0}}^{\prime }-{I_{1}}^{\prime }
\] であるから，①，⑤，$ \ {V_{0}}^{\prime }=\alpha E \ $を用いて整理すると，
\[
\begin{eqnarray}
{V_{1}}^{\prime } &=& {V_{0}}^{\prime }-2{I_{0}}^{\prime }-\frac {{I_{0}}^{\prime }}{2} \\[ 5pt ] &=& {V_{0}}^{\prime }-\frac {5}{2}{I_{0}}^{\prime } \\[ 5pt ] &=& {V_{0}}^{\prime }-\frac {1}{2}{V_{0}}^{\prime } \\[ 5pt ] &=& \frac {1}{2}{V_{0}}^{\prime }
\end{eqnarray}
\] となるので，$ \ \lambda =2 \ $と求められる。

※　他の回路も同様に求められます。以下参考として，図の回路の$ \ \mathrm {F} \ $行列を求めます。
回路図のNについて，
\[
\begin{bmatrix} {\dot V}_{1} \\ {\dot I}_{1} \end{bmatrix}=\begin{bmatrix} A & B \\ C & D \end{bmatrix}\begin{bmatrix} {\dot V}_{2} \\ {\dot I}_{2} \end{bmatrix}
\] とおくと，各$ \ \mathrm {F} \ $パラメータは，
\[
\begin{eqnarray}
\dot A &=& {{\dot V}_{1} \abovewithdelims . | 0.5pt {\dot V}_{2}}_{{\dot I}_{2}=0}=\frac {2+6}{6}=\frac {4}{3} \\[ 5pt ] \dot B &=& {{\dot V}_{1} \abovewithdelims . | 0.5pt {\dot I}_{2}}_{{\dot V}_{2}=0}=\frac {\displaystyle 2\times \frac {6+1}{6}{\dot I}_{2}+1\times {\dot I}_{2}}{{\dot I}_{2}}=\frac {10}{3} \ \mathrm {[\Omega ]} \\[ 5pt ] \dot C &=& {{\dot I}_{1} \abovewithdelims . | 0.5pt {\dot V}_{2}}_{{\dot I}_{2}=0}= \frac {{\dot I}_{1}}{6{\dot I}_{1}}=\frac {1}{6} \ \mathrm {[S]} \\[ 5pt ] \dot D &=& {{\dot I}_{1} \abovewithdelims . | 0.5pt {\dot I}_{2}}_{{\dot V}_{2}=0}=\frac{{\dot I}_{1}}{\displaystyle \frac {6}{6+1}{\dot I}_{1}}=\frac {7}{6}
\end{eqnarray}
\] と求められる。$ \ \mathrm {F} \ $行列の固有値$ \ \lambda \ $は，$ \ \mathrm{ det }\left( \dot F-\lambda \dot E\right) =0 \ $で求められるから，
\[
\begin{eqnarray}
\mathrm{ det }\left( \dot F-\lambda \dot E\right) &=& 0 \\[ 5pt ] \mathrm{ det } \begin{pmatrix} A-\lambda & B \\ C & D-\lambda \end{pmatrix} &=& 0 \\[ 5pt ] \mathrm{ det } \begin{pmatrix} \displaystyle \frac {4}{3}-\lambda & \displaystyle \frac {10}{3} \\ \displaystyle \frac {1}{6} & \displaystyle \frac {7}{6}-\lambda \end{pmatrix} &=& 0 \\[ 5pt ] \left( \frac {4}{3}-\lambda \right) \left( \frac {7}{6}-\lambda \right)-\frac {10}{3}\cdot \frac {1}{6} &=& 0 \\[ 5pt ] \lambda ^{2}-\frac {5}{2}\lambda +1 &=& 0 \\[ 5pt ] \lambda &=& 2, \frac {1}{2}
\end{eqnarray}
\] と求められる。

(2)解答：ル
(1)の通り，$ \ \lambda \ $と$ \ \lambda ^{-1} \ $は$ \ N \ $の$ \ \mathrm {F} \ $行列の固有値となります。

(3)解答：ロ
$ \ V_{2} \ $と$ \ I_{2} \ $の間に成り立つのはオームの法則です。電験一種だからもう少し難しい法則じゃないの！？といった問題です。(4点問題です。。。)

(4)解答：リ
$ \ V_{2}=V^{\prime}_{2}+V^{\prime\prime}_{2}=0 \ $に，$ \ \lambda =2 \ $と$ \ k=2 \ $のときの②，③式を代入すると，
\[
\begin{eqnarray}
V^{\prime}_{2}+V^{\prime\prime}_{2} &=& 0 \\[ 5pt ] 2^{-2}\alpha E+2^{2} (1-\alpha ) E &=& 0 \\[ 5pt ] \frac {1}{4}\alpha +4-4\alpha &=& 0 \\[ 5pt ] \alpha &=& \frac {16}{15}
\end{eqnarray}
\] と求められる。

(5)解答：ホ
②，③，$ \ \displaystyle \alpha =\frac {16}{15} \ $から，
\[
\begin{eqnarray}
I_{0} &=& I^{\prime }_{0}+I^{\prime\prime}_{0} \\[ 5pt ] &=& \lambda ^{-k}\frac {\alpha E}{5}-\lambda ^{k}\frac {(1-\alpha )E}{4} \\[ 5pt ] &=& 2 ^{-0}\frac {\frac {16}{15} E}{5}-2 ^{0}\frac {(1-\frac {16}{15} )E}{4} \\[ 5pt ] &=& \frac {16}{75}E+\frac {1}{60}E \\[ 5pt ] &=& \frac {23}{100}E
\end{eqnarray}
\] と求められる。