【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,ポインティングベクトルに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
誘電率,透磁率及び導電率がそれぞれ\( \ \varepsilon \ \),\( \ \mu \ \)及び\( \ \sigma \ \)で一様な微小領域\( \ V \ \)を想定する。\( \ V \ \)内において電界及び磁界は一様であり,時刻\( \ t \ \)における電界ベクトルが\( \ \vec{ E } \ \),磁界ベクトルが\( \ \vec{ H } \ \)であるとき,\( \ V \ \)内の単位体積当たりの電磁界エネルギー\( \ u \ \)は\( \ \fbox { (1) } \ \)と表される。
ここで,\( \ \sigma =0 \ \)のとき,\( \ u \ \)の単位時間当たりの変化量\( \ \displaystyle \frac{ \partial u }{ \partial t } \ \)は,単位面積当たりのエネルギーの流れ\( \ \vec{ S } \ \)を用いて\( \ \displaystyle \frac{ \partial u }{ \partial t }= \ \fbox { (2) } \ \)と表される。\( \ \vec{ S } \ \)はポインティングベクトルと呼ばれ,\( \ \vec{ S }=\ \fbox { (3) } \ \)と表される。\( \ \vec{ E } \ \)及び\( \ \vec{ H } \ \)が直交座標系\( \ \left( x,y,z \right) \ \)において,それぞれ\( \ \vec{ E }=\left( E_{x},0,0 \right) \ \),\( \ \vec{ H }=\left( 0,H_{y},0 \right) \ \)と表されるとき,\( \ \vec{ S } \ \)は\( \ \fbox { (4) } \ \)軸と平行である。
また,\( \ \sigma ≠0 \ \)のときは,\( \ \displaystyle \frac{ \partial u }{ \partial t }= \ \fbox { (2) } \ – \ \fbox { (5) } \ \)と表される。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \vec{ E }\cdot \vec{ H } &(ロ)& \vec{ H }\times \vec{ E } &(ハ)& \sigma \left| \vec{ E }\right| ^{2} \\[ 5pt ]
&(ニ)& -\nabla \cdot \vec{ S } &(ホ)& \vec{ E }\times \vec{ H } &(ヘ)& x \\[ 5pt ]
&(ト)& \sigma \vec{ E }\cdot \vec{ H } &(チ)& \nabla \cdot \vec{ S } &(リ)& \frac {1}{2}\sigma \left| \vec{ E }\right| ^{2}+\frac {1}{2}\mu \left| \vec{ H }\right| ^{2} \\[ 5pt ]
&(ヌ)& \frac {1}{2}\varepsilon \left| \vec{ E }\right| ^{2}+\frac {1}{2}\mu \left| \vec{ H }\right| ^{2} &(ル)& \frac {1}{2}\vec{ E }\cdot \vec{ H } &(ヲ)& y \\[ 5pt ]
&(ワ)& \nabla \times \vec{ S } &(カ)& \sigma \left| \vec{ E }\right| &(ヨ)& z \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
ポインティングベクトルの演算に関する問題です。
電磁気学の教科書には掲載されている内容ですが,\( \ 2 \ \)種までの電験のテキストにはまず掲載されていない内容なので,厳しい問題であったかと思います。
ポインティングベクトルは電磁波のエネルギーの流れのようなもので,この定義は理解しておくようにしましょう。
1.\( \ \mathrm {grad} \ \)(勾配)
数学における\( \ \mathrm {grad} \ \)(勾配)は,
\[
\begin{eqnarray}
\mathrm {grad} V&=&\nabla V
&=&\left( \frac { \partial V}{ \partial x },\frac { \partial V}{ \partial y },\frac { \partial V}{ \partial z }\right) \\[ 5pt ]
\end{eqnarray}
\]
で定義されます。\( \ \nabla \ \)は数学で\( \ \displaystyle \nabla =\frac { \partial }{ \partial x }\boldsymbol i+\frac { \partial }{ \partial y }\boldsymbol j+\frac { \partial }{ \partial z }\boldsymbol k \ \)で定義される演算子です。
(\( \ \boldsymbol i \ \),\( \ \boldsymbol j \ \),\( \ \boldsymbol k \ \)は\( \ x \ \)軸,\( \ y \ \)軸,\( \ z \ \)軸の単位ベクトルです)
2.\( \ \mathrm {div} \ \)(発散)
数学における\( \ \mathrm {div} \ \)(発散)は,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E&=&\frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y } +\frac { \partial E_{\mathrm {z}}}{ \partial z } \\[ 5pt ]
\end{eqnarray}
\]
で定義され,内積を用いて表すと,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E &=& \nabla \cdot \boldsymbol E \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.\( \ \mathrm {rot} \ \)(回転)
数学における\( \ \mathrm {rot} \ \)(回転)は,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol E&=&\left( \frac { \partial E_{\mathrm {z}}}{ \partial y }-\frac { \partial E_{\mathrm {y}}}{ \partial z },\frac { \partial E_{\mathrm {x}}}{ \partial z }-\frac { \partial E_{\mathrm {z}}}{ \partial x },\frac { \partial E_{\mathrm {y}}}{ \partial x }-\frac { \partial E_{\mathrm {x}}}{ \partial y }\right) \\[ 5pt ]
\end{eqnarray}
\]
で定義され,外積を用いて表すと,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol E &=& \nabla \times \boldsymbol E \\[ 5pt ]
&=& \begin{vmatrix} \boldsymbol i & \boldsymbol j & \boldsymbol k \\ \displaystyle \frac { \partial }{ \partial x } & \displaystyle \frac { \partial }{ \partial y } & \displaystyle \frac { \partial }{ \partial z } \\ E_{\mathrm {x}} & E_{\mathrm {y}} & E_{\mathrm {z}} \end{vmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.マクスウェル方程式(微分形)
電磁気における各性質を4つの式にまとめたものです。
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol D &=&\rho &⇔& \nabla \cdot \boldsymbol D &=&\rho \\[ 5pt ]
\mathrm {div} \boldsymbol B &=&0 &⇔& \nabla \cdot \boldsymbol B &=&0 \\[ 5pt ]
\mathrm {rot} \boldsymbol H &=&i+\displaystyle \frac { \partial \boldsymbol D}{ \partial t } &⇔& \nabla \times \boldsymbol H &=&i+\displaystyle \frac { \partial \boldsymbol D}{ \partial t } \\[ 5pt ]
\mathrm {rot} \boldsymbol E &=&-\displaystyle \frac { \partial \boldsymbol B}{ \partial t } &⇔& \nabla \times \boldsymbol E &=&-\displaystyle \frac { \partial \boldsymbol B}{ \partial t } \\[ 5pt ]
\end{eqnarray}
\]
5.ポインティングベクトル
ポインティングベクトルは電界\( \ \vec {E} \ \)及び磁界\( \ \vec {H} \ \)の外積で定義される物理量で,電磁エネルギーの流れの向きとなり,電界と磁界の向きが与えられているとすると,図1の通り,その両方の成分と直角の向きとなります。電界から磁界に向かって右ねじを回すとき,右ねじが進む向きがポインティングベクトルの向きとなります。
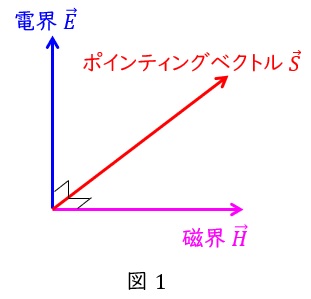
6.エネルギー密度\( \ w \ \)
一様電界中の電界の大きさが\( \ \boldsymbol E \ \mathrm {[V / m]} \ \),電束密度が\( \ \boldsymbol D \ \mathrm {[C / m^{2}]} \ \),誘電率が\( \ \varepsilon \ \mathrm {[F / m]} \ \)であるとき,静電エネルギー密度\( \ w_{\mathrm {e}} \ \mathrm {[J / m^{3}]} \ \)は,
\[
\begin{eqnarray}
w_{\mathrm {e}} &=&\frac {1}{2}\boldsymbol D\cdot \boldsymbol E \\[ 5pt ]
&=&\frac {1}{2}\varepsilon \left| \boldsymbol E\right| ^{2} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。また,一様磁界中の磁界の大きさ\( \ \boldsymbol H \ \mathrm {[A / m]} \ \),磁束密度が\( \ \boldsymbol B \ \mathrm {[T]} \ \),誘電率が\( \ \mu \ \mathrm {[H / m]} \ \)であるとき,磁気エネルギー密度\( \ w_{\mathrm {h}} \ \mathrm {[J / m^{3}]} \ \)は,
\[
\begin{eqnarray}
w_{\mathrm {h}} &=&\frac {1}{2}\boldsymbol H\cdot \boldsymbol B \\[ 5pt ]
&=&\frac {1}{2}\mu \left| \boldsymbol H\right| ^{2} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:ヌ
ワンポイント解説「6.エネルギー密度\( \ w \ \)」の通り,単位体積当たりの電磁界エネルギー\( \ u \ \)は,
\[
\begin{eqnarray}
u &=&\frac {1}{2}\varepsilon \left| \vec{ E }\right| ^{2}+\frac {1}{2}\mu \left| \vec{ H }\right| ^{2} \\[ 5pt ]
\end{eqnarray}
\]
で求められる。
(2)解答:ニ
(1)解答式より,一様な電界及び磁界においては,
\[
\begin{eqnarray}
\frac{ \partial u }{ \partial t } &=&\frac{ \partial }{ \partial t }\left( \frac {1}{2}\varepsilon \left| \vec{ E }\right| ^{2}+\frac {1}{2}\mu \left| \vec{ H }\right| ^{2} \right) \\[ 5pt ]
&=& \varepsilon \vec{ E }\cdot \frac{ \partial \vec{ E } }{ \partial t }+ \mu \vec{ H }\cdot \frac{ \partial \vec{ H } }{ \partial t } \\[ 5pt ]
&=& \vec{ E }\cdot \frac{ \partial \vec{ D } }{ \partial t }+ \vec{ H }\cdot \frac{ \partial \vec{ B } }{ \partial t } \\[ 5pt ]
\end{eqnarray}
\]
と変形でき,ワンポイント解説「4.マクスウェル方程式(微分形)」より,\( \ \sigma =0 \ \)においては\( \ i=0 \ \)となるので,
\[
\begin{eqnarray}
\frac{ \partial u }{ \partial t } &=&\vec{ E }\cdot \nabla \times \vec{ H }-\vec{ H }\cdot \nabla \times \vec{ E } \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,数学のベクトルの公式\( \ \nabla \left( \vec{ E }\times \vec{ H } \right) =\vec{ H }\cdot \nabla \times \vec{ E } -\vec{ E }\cdot \nabla \times \vec{ H } \ \)を用いると,
\[
\begin{eqnarray}
\frac{ \partial u }{ \partial t } &=&-\nabla \left( \vec{ E }\times \vec{ H } \right) \\[ 5pt ]
&=&-\nabla \vec{ S } \\[ 5pt ]
\end{eqnarray}
\]
となる。
※試験においては,本導出は不要で覚えておく内容となります。
(3)解答:ホ
ワンポイント解説「5.ポインティングベクトル」の通り,\( \ \vec{ S }=\vec{ E }\times \vec{ H } \ \)となる。
(4)解答:ヨ
ワンポイント解説「5.ポインティングベクトル」の通り,\( \ \vec{ E } \ \)が\( \ x \ \)軸方向及び\( \ \vec{ H } \ \)が\( \ y \ \)軸方向なので,\( \ \vec{ S } \ \)が\( \ z \ \)軸方向となる。
(5)解答:ハ
\( \ \sigma ≠0 \ \)のときは,電流密度\( \ \vec{ J }=\sigma \vec{ E } \ \)の関係があるので,\( \ u \ \)の単位時間当たりの変化量は,
\[
\begin{eqnarray}
\frac{ \partial u }{ \partial t } &=&-\nabla \vec{ S }-\vec{ J } \vec{ E } \\[ 5pt ]
&=&-\nabla \vec{ S }-\sigma \left| \vec{ E } \right| ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん