《理論》〈電磁気〉[H20:問5]円柱導体内部に蓄えられる磁気エネルギーに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，十分に長い円柱導体に一様に電流が流れているときの導体内部に蓄えられる磁気エネルギーに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式を解答群の中から選び，その記号を記述用紙の解答欄に記入しなさい。

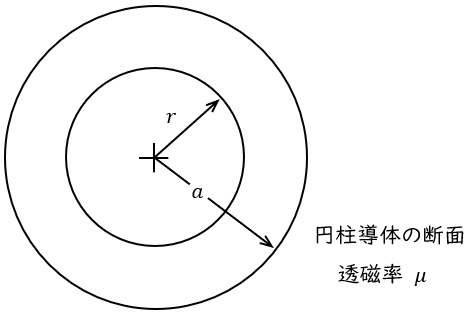
図のように，透磁率が$ \ \mu \ $の材料からなる半径$ \ a \ $の十分に長い円柱導体に，電流密度が一様な直流電流$ \ I \ $を流すことを考える。このとき，円柱導体の単位長さ当たりの磁気エネルギーを求めてみよう。

円柱の中心から半径$ \ r \ $の円内を通る電流は$ \ \fbox {　（１）　} \ $であるから，中心から$ \ r \ $の位置の磁界の強さは$ \ \fbox {　（２）　} \ $となる。したがって，そこでの単位体積当たりの磁気エネルギー$ \ W_{0} \ $は$ \ \fbox {　（３）　} \ $と計算される。これより，求める円柱導体の単位長さ当たりの磁気エネルギー$ \ W \ $は$ \ W_{0} \ $を$ \ \fbox {　（４）　} \ $式のように半径$ \ r \ $について$ \ 0 \ $から$ \ a \ $まで積分して，$ \ \fbox {　（５）　} \ $となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\mu a}{32\pi }I^{2}　　　　　&（ロ）&　\frac {r}{2\pi a^{2}}I　　　　　&（ハ）&　\int _{0}^{a} \pi r W_{0}\mathrm {d}r \\[ 5pt ] &（ニ）&　\frac {r}{a}I　　　　　　　&（ホ）&　\frac {\mu }{32\pi }I^{2}　　　　　&（ヘ）&　\frac {\mu I^{2}}{8\pi ^{2}a^{4}}r^{2} \\[ 5pt ] &（ト）&　\frac {r^{2}}{a^{2}}I　　　　　&（チ）&　\frac {\mu I^{4}}{8\pi ^{2}a^{4}}r^{2}　　　　　　　&（リ）&　\frac {\mu I^{2}}{8\pi ^{2}a^{2}}r^{2} \\[ 5pt ] &（ヌ）&　\int _{0}^{a} \pi r^{2} W_{0}\mathrm {d}r　　　　　&（ル）&　\int _{0}^{a} 2\pi r W_{0}\mathrm {d}r　　　　　&（ヲ）&　\frac {r^{2}}{a^{2}}I^{2} \\[ 5pt ] &（ワ）&　\frac {\mu }{16\pi }I^{2}　　　　　&（カ）&　\frac {r}{2\pi a^{2}}I^{2}　　　　　　&（ヨ）&　\frac {1}{2\pi a}I \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

導体中に電流が流れているときに蓄えられる磁気エネルギーを求める問題です。
内側に流れる電流やエネルギー密度等電磁気の積分の考え方を理解する上ではとても良い問題と言えると思います。
配点の高い問5としては比較的取り組みやすい問題なので，ぜひとも高得点を狙いたい問題です。

1.アンペア（アンペール）の周回積分の法則
空間上の磁界ベクトルを$ \ \boldsymbol H \ \mathrm {[A / m]} \ $，$ \ \mathrm {C} \ $を閉曲線，$ \ \mathrm {d}\boldsymbol l \ $を$ \ \mathrm {C} \ $上の微小区間ベクトル，$ \ I \ \mathrm {[A]} \ $を$ \ \mathrm {C} \ $と鎖交する電流の総量とすると，
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I　 \\[ 5pt ] \end{eqnarray}
\] の関係があり，これをアンペアの周回積分の法則といいます。
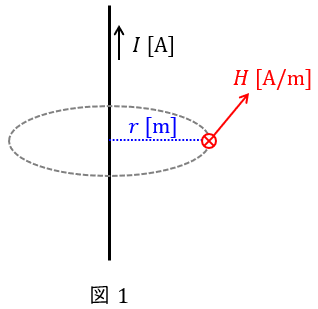
例えば，図1のように無限長直線電流$ \ I \ \mathrm {[A]} \ $が流れているとき，電線から距離$ \ r \ \mathrm {[m]} \ $の位置での磁界の強さ$ \ H \ \mathrm {[A / m]} \ $は，$ \ l=2\pi r \ $なので，
\[
\begin{eqnarray}
2\pi r H&=&I \\[ 5pt ] H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.エネルギー密度$ \ w \ $
一様電界中の電界の大きさが$ \ \boldsymbol E \ \mathrm {[V / m]} \ $，電束密度が$ \ \boldsymbol D \ \mathrm {[C / m^{2}]} \ $，誘電率が$ \ \varepsilon \ \mathrm {[F / m]} \ $であるとき，静電エネルギー密度$ \ w_{\mathrm {e}} \ \mathrm {[J / m^{3}]} \ $は，
\[
\begin{eqnarray}
w_{\mathrm {e}} &=&\frac {1}{2}\boldsymbol D\cdot \boldsymbol E \\[ 5pt ] &=&\frac {1}{2}\varepsilon \left| \boldsymbol E\right| ^{2} \\[ 5pt ] \end{eqnarray}
\] で求められます。また，一様磁界中の磁界の大きさ$ \ \boldsymbol H \ \mathrm {[A / m]} \ $，磁束密度が$ \ \boldsymbol B \ \mathrm {[T]} \ $，透磁率が$ \ \mu \ \mathrm {[H / m]} \ $であるとき，磁気エネルギー密度$ \ w_{\mathrm {h}} \ \mathrm {[J / m^{3}]} \ $は，
\[
\begin{eqnarray}
w_{\mathrm {h}} &=&\frac {1}{2}\boldsymbol H\cdot \boldsymbol B \\[ 5pt ] &=&\frac {1}{2}\mu \left| \boldsymbol H\right| ^{2} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)解答：ト
導体内を一様に電流が流れているので，半径$ \ r \ $の内側を流れる電流の大きさ$ \ I_{r} \ $は，
\[
\begin{eqnarray}
I_{r} &=&\frac {\pi r^{2}}{\pi a^{2}}I \\[ 5pt ] &=&\frac {r^{2}}{a^{2}}I \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ロ
(1)より，中心から$ \ r \ $の位置の磁界の強さ$ \ H_{r} \ $は，ワンポイント解説「1.アンペア（アンペール）の周回積分の法則」の通り，
\[
\begin{eqnarray}
H_{r}&=&\frac {I_{r}}{2\pi r} \\[ 5pt ] &=&\frac {\displaystyle \frac {r^{2}}{a^{2}}I}{2\pi r} \\[ 5pt ] &=&\frac {r}{2\pi a^{2}}I \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヘ
(2)より，単位体積当たりの磁気エネルギー$ \ W_{0} \ $は，ワンポイント解説「2.エネルギー密度$ \ w \ $」の通り，
\[
\begin{eqnarray}
W_{0} &=&\frac {1}{2}\mu H_{r} ^{2} \\[ 5pt ] &=&\frac {1}{2}\mu \left( \frac {r}{2\pi a^{2}}I\right) ^{2} \\[ 5pt ] &=&\frac {\mu I^{2}}{8\pi ^{2}a^{4}}r^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
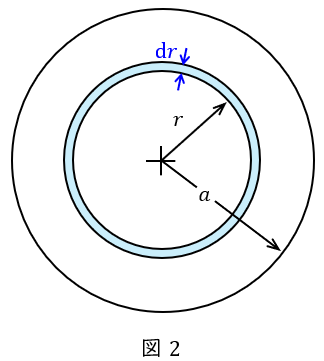
図2に示すように，中心からの距離$ \ r \ $から$ \ r+\mathrm {d}r \ $までの単位長さ当たりの体積$ \ \mathrm {d}V \ $は，
\[
\begin{eqnarray}
\mathrm {d}V &=&2\pi r\cdot \mathrm {d}r \cdot 1 \\[ 5pt ] &=&2\pi r \mathrm {d}r \\[ 5pt ] \end{eqnarray}
\] であるから，円柱導体の単位長さあたりの磁気エネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W &=&\int W_{0}\mathrm {d}V \\[ 5pt ] &=&\int _{0}^{a} W_{0} \cdot 2\pi r \mathrm {d}r \\[ 5pt ] &=&\int _{0}^{a} 2\pi r W_{0} \mathrm {d}r \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ワ
(4)解答式より，
\[
\begin{eqnarray}
W &=&\int _{0}^{a} 2\pi r \cdot \frac {\mu I^{2}}{8\pi ^{2}a^{4}}r^{2} \mathrm {d}r \\[ 5pt ] &=&\int _{0}^{a} \frac {\mu I^{2}}{4\pi a^{4}}r^{3} \mathrm {d}r \\[ 5pt ] &=&\frac {\mu I^{2}}{4\pi a^{4}}\int _{0}^{a} r^{3} \mathrm {d}r \\[ 5pt ] &=&\frac {\mu I^{2}}{4\pi a^{4}}\left[ \frac {r^{4}}{4}\right] _{0}^{a} \\[ 5pt ] &=&\frac {\mu I^{2}}{4\pi a^{4}}\cdot \frac {a^{4}}{4} \\[ 5pt ] &=&\frac {\mu }{16\pi }I^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。