【問題】
【難易度】★★★☆☆(普通)
次の文章は,直流回路の合成抵抗に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
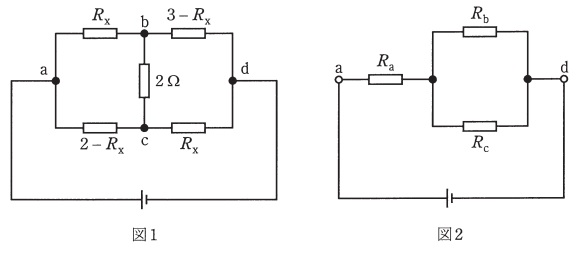
図1に示す回路の合成抵抗を求めたい。まず,節点\( \ \mathrm {a-b-c} \ \)からなる\( \ \mathrm {\Delta } \ \)接続部分に「\( \ \mathrm {\Delta – Y} \ \)変換」を施すと,図1の\( \ \mathrm {a-d} \ \)間の抵抗は図2のように表すことができる。
図2の\( \ R_{\mathrm {a}} \ \),\( \ R_{\mathrm {b}} \ \),\( \ R_{\mathrm {c}} \ \)は,\( \ R_{\mathrm {x}} \ \)を用いて\( \ R_{\mathrm {a}}= \ \fbox { (1) } \ [\Omega ] \ \),\( \ R_{\mathrm {b}}= \ \fbox { (2) } \ [\Omega ] \ \),\( \ R_{\mathrm {c}}= \ \fbox { (3) } \ [\Omega ] \ \)となる。
したがって,回路全体の合成抵抗\( \ R_{\mathrm {ad}} \ \)は,\( \ R_{\mathrm {ad}}= \ \fbox { (4) } \ [\Omega ] \ \)と表され,\( \ R_{\mathrm {x}}= \ \fbox { (5) } \ [\Omega ] \ \)において最大となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{\mathrm {x}}+6}{2} &(ロ)& \frac {R_{\mathrm {x}}+2}{2} &(ハ)& \frac {-R_{\mathrm {x}}^{2}+2R_{\mathrm {x}}}{4} \\[ 5pt ]
&(ニ)& \frac {-R_{\mathrm {x}}+2}{2} &(ホ)& 0.5 &(ヘ)& 1.2 \\[ 5pt ]
&(ト)& \frac {-R_{\mathrm {x}}+3}{4} &(チ)& \frac {R_{\mathrm {x}}^{2}}{2} &(リ)& 2 \\[ 5pt ]
&(ヌ)& \frac {-5R_{\mathrm {x}}^{2}+12R_{\mathrm {x}}+12}{16} &(ル)& \frac {R_{\mathrm {x}}+2}{4} &(ヲ)& \frac {R_{\mathrm {x}}^{2}}{R_{\mathrm {x}}+1} \\[ 5pt ]
&(ワ)& \frac {-R_{\mathrm {x}}+6}{2} &(カ)& \frac {11R_{\mathrm {x}}^{2}+44R_{\mathrm {x}}+12}{4} &(ヨ)& \frac {11R_{\mathrm {x}}^{2}+12R_{\mathrm {x}}+12}{4}
\end{eqnarray}
\]
【ワンポイント解説】
不平衡回路の\( \ \mathrm {\Delta – Y} \ \)変換は電験一種では毎年のように出題されます。なかなか覚えにくい公式ですが,電験一種試験前には確実にマスターしておいて下さい。本問の場合は\( \ \mathrm {\Delta – Y} \ \)変換を知っているかどうかで10点の差がついてしまいます。
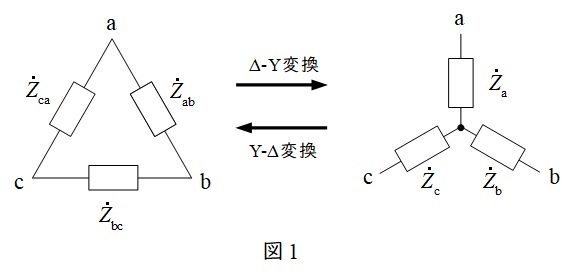
1.不平衡負荷の\( \ \mathrm {\Delta – Y} \ \)変換と\( \ \mathrm {Y – \Delta} \ \)変換
a.\( \ \mathrm {\Delta – Y} \ \)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}} &=& \frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}} &=& \frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}}
\end{eqnarray}
\]
b.\( \ \mathrm {Y – \Delta} \ \)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}}
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)解答:ハ
ワンポイント解説「1.不平衡負荷の\( \ \mathrm {\Delta – Y} \ \)変換と\( \ \mathrm {Y – \Delta} \ \)変換」より,回路\( \ \mathrm {a-b-c} \ \)に「\( \ \mathrm {\Delta – Y} \ \)変換」を適用すると,
\[
\begin{eqnarray}
{R}_{\mathrm {a}} &=& \frac {{R}_{\mathrm {x}}\left( 2-R_{\mathrm {x}}\right) }{{R}_{\mathrm {x}}+2+\left( 2-R_{\mathrm {x}}\right) } \\[ 5pt ]
&=& \frac {-R_{\mathrm {x}}^{2}+2R_{\mathrm {x}}}{4}
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
\( \ R_{\mathrm {b}} \ \)は,(1)と同様に「\( \ \mathrm {\Delta – Y} \ \)変換」をして,抵抗\( \ 3-R_{\mathrm {x}} \ \)を合成したものであるから,
\[
\begin{eqnarray}
{R}_{\mathrm {b}} &=& \frac {{R}_{\mathrm {x}}\cdot 2 }{{R}_{\mathrm {x}}+2+\left( 2-R_{\mathrm {x}}\right) }+3-R_{\mathrm {x}} \\[ 5pt ]
&=& \frac {R_{\mathrm {x}}}{2}+3-R_{\mathrm {x}} \\[ 5pt ]
&=& \frac {-R_{\mathrm {x}}+6}{2}
\end{eqnarray}
\]
と求められる。
(3)解答:ロ
\( \ R_{\mathrm {c}} \ \)は,(1),(2)と同様に「\( \ \mathrm {\Delta – Y} \ \)変換」をして,抵抗\( \ R_{\mathrm {x}} \ \)を合成したものであるから,
\[
\begin{eqnarray}
{R}_{\mathrm {c}} &=& \frac {2\left( 2-R_{\mathrm {x}}\right) }{{R}_{\mathrm {x}}+2+\left( 2-R_{\mathrm {x}}\right) }+R_{\mathrm {x}} \\[ 5pt ]
&=& \frac {-R_{\mathrm {x}}+2}{2}+R_{\mathrm {x}} \\[ 5pt ]
&=& \frac {R_{\mathrm {x}}+2}{2}
\end{eqnarray}
\]
と求められる。
(4)解答:ヌ
図2より,回路全体の合成抵抗\( \ R_{\mathrm {ad}} \ \)は,
\[
R_{\mathrm {ad}}=R_{\mathrm {a}}+\frac {R_{\mathrm {b}}R_{\mathrm {c}}}{R_{\mathrm {b}}+R_{\mathrm {c}}}
\]
であるから,(1)~(3)より\( \ R_{\mathrm {a}} \ \),\( \ R_{\mathrm {b}} \ \),\( \ R_{\mathrm {c}} \ \)にそれぞれ解答式を代入すると,
\[
\begin{eqnarray}
R_{\mathrm {ad}} &=& R_{\mathrm {a}}+\frac {R_{\mathrm {b}}R_{\mathrm {c}}}{R_{\mathrm {b}}+R_{\mathrm {c}}} \\[ 5pt ]
&=& \frac {-R_{\mathrm {x}}^{2}+2R_{\mathrm {x}}}{4}+\frac {\displaystyle \frac {-R_{\mathrm {x}}+6}{2}\cdot \frac {R_{\mathrm {x}}+2}{2}}{\displaystyle \frac {-R_{\mathrm {x}}+6}{2}+\frac {R_{\mathrm {x}}+2}{2}} \\[ 5pt ]
&=& \frac {-R_{\mathrm {x}}^{2}+2R_{\mathrm {x}}}{4}+\frac {-R_{\mathrm {x}}^{2}+4R_{\mathrm {x}}+12}{16} \\[ 5pt ]
&=& \frac {-5R_{\mathrm {x}}^{2}+12R_{\mathrm {x}}+12}{16}
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
\( \ R_{\mathrm {ad}} \ \)が最大値となるためには,\( \ \displaystyle \frac {\mathrm {d} R_{\mathrm {ad}}}{\mathrm {d} R_{\mathrm {x}}}=0 \ \)とならなければならない。よって,(4)の解答式の両辺を微分して,\( \ \displaystyle \frac {\mathrm {d} R_{\mathrm {ad}}}{\mathrm {d} R_{\mathrm {x}}}=0 \ \)となる\( \ R_{\mathrm {x}} \ \)を求めると,
\[
\begin{eqnarray}
\frac {\mathrm {d} R_{\mathrm {ad}}}{\mathrm {d} R_{\mathrm {x}}} = \frac {1}{16}\left( -10R_{\mathrm {x}}+12\right) &=& 0\\[ 5pt ]
∴ R_{\mathrm {x}}&=& 1.2
\end{eqnarray}
\]
と求められる。
※ブリッジの平衡条件と一致しています。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん