【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,直流電圧源に接続された\( \ 2 \ \)端子対抵抗回路に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。
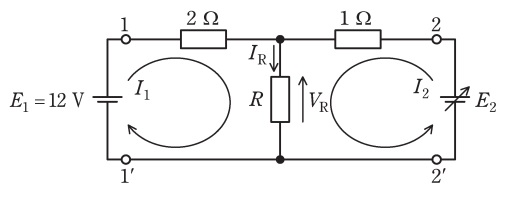
図のように未知抵抗\( \ R \ \)を含む\( \ 2 \ \)端子対抵抗回路の端子対\( \ 1-1^{\prime } \ \)に直流電圧源\( \ E_{1} \ \)を接続し,端子対\( \ 2-2^{\prime } \ \)に可変直流電圧源\( \ E_{2} \ \)を接続した。図の回路の抵抗で消費される電力を\( \ P \ \)とする。
図のように閉路電流\( \ I_{1} \ \),\( \ I_{2} \ \)を定めると,閉路方程式は,
\[
\begin{eqnarray}
\begin{bmatrix} E_{1} \\ E_{2} \end{bmatrix} &=& \fbox { (1) }\begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \fbox { (1) } \ \)の行列は図の\( \ 2 \ \)端子対抵抗回路の\( \ \mathrm {Z} \ \)行列と一致する。
\( \ E_{1}=12 \ \mathrm {V} \ \)とし,可変直流電圧源の電圧\( \ E_{2} \ \)を変化させると以下の結果が得られた。
(a) \( \ E_{2}=15 \ \mathrm {V} \ \)のとき,\( \ I_{1} \ \)は零となった。
(b) \( \ E_{2}=8 \ \mathrm {V} \ \)のとき,\( \ P \ \)は最小値\( \ 24 \ \mathrm {W} \ \)となった。
(c) \( \ E_{2} \ \)を\( \ 8 \ \mathrm {V} \ \)より小さなある値にすると,\( \ I_{\mathrm {R}}=1 \ \mathrm {A} \ \)となった。
(a)のときの電流\( \ I_{2} \ \)は,\( \ V_{\mathrm {R}}=E_{1} \ \)であるから\( \ I_{2}=\fbox { (2) } \ \mathrm {A} \ \)となる。また,未知抵抗\( \ R \ \)の値は\( \ R=\fbox { (3) } \ \mathrm {\Omega } \ \)となる。
(b)のときの電流\( \ I_{1} \ \),\( \ I_{2} \ \)は,閉路方程式と\( \ R=\fbox { (3) } \ \mathrm {\Omega } \ \)より,
\[
\begin{eqnarray}
\begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} &=& \fbox { (4) } \ \mathrm {A} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(c)のときの\( \ E_{2} \ \)は,\( \ V_{\mathrm {R}} \ \),\( \ I_{1} \ \)及び\( \ I_{2} \ \)を計算すると,\( \ E_{2}=\fbox { (5) } \ \mathrm {V} \ \)となる。このときの消費電力\( \ P \ \)を計算すると,(a)と同じ値になることが分かる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 2 &(ロ)& \begin{bmatrix} 2+R & R \\ -R & 1+R \end{bmatrix} &(ハ)& \begin{bmatrix} 3 \\ -1.5 \end{bmatrix} \\[ 5pt ]
&(ニ)& \begin{bmatrix} 1 \\ 1.5 \end{bmatrix} &(ホ)& -3 &(ヘ)& \begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix} \\[ 5pt ]
&(ト)& 4 &(チ)& 6 &(リ)& 1 \\[ 5pt ]
&(ヌ)& 5 &(ル)& \begin{bmatrix} 2 \\ 0 \end{bmatrix} &(ヲ)& \begin{bmatrix} 2+R & -R \\ -R & 1+R \end{bmatrix} \\[ 5pt ]
&(ワ)& 3 &(カ)& -2 &(ヨ)& -1 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
例年三相の不平衡回路が出題されやすい問5ですが,昨年の反動なのかB問題としてはかなり易しい問題が出題されました。\( \ \mathrm {Z} \ \)行列の定義と逆行列の計算ができれば,あとは特に難しい数学は使用しません。配点が大きいので,計算ミスには十分に注意しましょう。
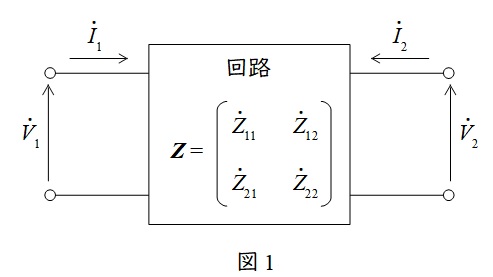
1.\( \ \mathrm {Z} \ \)行列(インピーダンス行列)
図1に示すような2端子対回路があり,各電流電圧を図のように定めた時,
\[
\begin{eqnarray}
\begin{bmatrix} V_{1} \\ V_{2} \end{bmatrix} &=& \begin{bmatrix} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
で表される行列\( \ \displaystyle \boldsymbol Z =\begin{bmatrix} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{bmatrix} \ \)を\( \ \mathrm {Z} \ \)行列と言います。各値は以下のようにして求められます。
\[
\begin{eqnarray}
Z_{11} &=& \left. \frac {V_{1}}{I_{1}}\right| _{I_{2}=0} \\[ 5pt ]
Z_{12} &=& \left. \frac {V_{1}}{I_{2}}\right| _{I_{1}=0} \\[ 5pt ]
Z_{21} &=& \left. \frac {V_{2}}{I_{1}}\right| _{I_{2}=0} \\[ 5pt ]
Z_{22} &=& \left. \frac {V_{2}}{I_{2}}\right| _{I_{1}=0} \\[ 5pt ]
\end{eqnarray}
\]
2.逆行列\( \ \boldsymbol A^{-1} \ \)
ある行列\( \ \displaystyle \boldsymbol A =\begin{bmatrix} a & b \\ c & d \end{bmatrix} \ \)が与えられているとき,\( \ \boldsymbol A \ \)の逆行列\( \ \boldsymbol A^{-1} \ \)は
\[
\begin{eqnarray}
\boldsymbol A^{-1} &=& \frac {1}{ad-bc}\begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。逆行列の特徴として,
\[
\begin{eqnarray}
\boldsymbol A^{-1}\cdot \boldsymbol A &=& \frac {1}{ad-bc}\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix} \\[ 5pt ]
&=& \frac {1}{ad-bc}\begin{bmatrix} ad-bc & 0 \\ 0 & ad-bc \end{bmatrix} \\[ 5pt ]
&=& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\boldsymbol A\cdot \boldsymbol A^{-1} &=& \begin{bmatrix} a & b \\ c & d \end{bmatrix}\frac {1}{ad-bc}\begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \\[ 5pt ]
&=& \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} \displaystyle \frac {d}{ad-bc} & \displaystyle -\frac {b}{ad-bc} \\ \displaystyle -\frac {c}{ad-bc} & \displaystyle \frac {a}{ad-bc} \end{bmatrix} \\[ 5pt ]
&=& \begin{bmatrix} \displaystyle \frac {ad-bc}{ad-bc} & \displaystyle \frac {-ab+ab}{ad-bc} \\ \displaystyle \frac {cd-cd}{ad-bc} & \displaystyle \frac {-bc+ad}{ad-bc} \end{bmatrix} \\[ 5pt ] \\[ 5pt ]
&=& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,逆行列を掛けることで単位行列となる特徴があります。
【解答】
(1)解答:ヘ
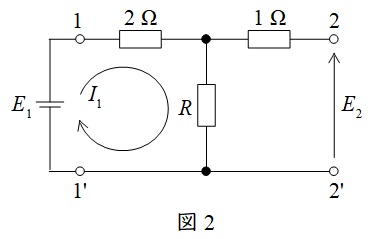
ワンポイント解説「1.\( \ \mathrm {Z} \ \)行列(インピーダンス行列)」より,\( \ Z_{11} \ \)は図2のように開放し,\( \ I_{2}=0 \ \)としたような回路により求めれば良いので,
\[
\begin{eqnarray}
Z_{11} &=& \left. \frac {E_{1}}{I_{1}}\right| _{I_{2}=0} \\[ 5pt ]
&=& \frac {\left( 2+R\right) I_{1}}{I_{1}} \\[ 5pt ]
&=& 2+R \\[ 5pt ]
\end{eqnarray}
\]
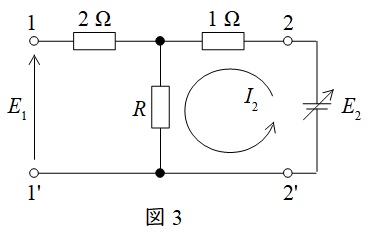
と求められる。\( \ Z_{12} \ \)は図3のように開放し,\( \ I_{1}=0 \ \)としたような回路により求めれば良いので,
\[
\begin{eqnarray}
Z_{12} &=& \left. \frac {E_{1}}{I_{2}}\right| _{I_{1}=0} \\[ 5pt ]
&=& \frac {RI_{2}}{I_{2}} \\[ 5pt ]
&=& R \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\( \ Z_{21} \ \)は図2のように開放し,\( \ I_{2}=0 \ \)としたような回路により求めれば良いので,
\[
\begin{eqnarray}
Z_{21} &=& \left. \frac {E_{2}}{I_{1}}\right| _{I_{2}=0} \\[ 5pt ]
&=& \frac {RI_{1}}{I_{1}} \\[ 5pt ]
&=& R \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\( \ Z_{22} \ \)は図3のように開放し,\( \ I_{1}=0 \ \)としたような回路により求めれば良いので,
\[
\begin{eqnarray}
Z_{22} &=& \left. \frac {E_{2}}{I_{2}}\right| _{I_{1}=0} \\[ 5pt ]
&=& \frac {\left( 1+R\right) I_{2}}{I_{2}} \\[ 5pt ]
&=& 1+R \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,\( \ \mathrm {Z} \ \)行列は,
\[
\begin{eqnarray}
\boldsymbol Z &=& \begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
(3)解答:ト
(a)の条件の時,各値を代入すると,
\[
\begin{eqnarray}
\begin{bmatrix} 12 \\ 15 \end{bmatrix} &=& \begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix}\begin{bmatrix} 0 \\ I_{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
12 = RI_{2} \\[ 5pt ]
15 = \left( 1+R \right) I_{2} \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
と連立方程式を立てることができ,これを解くと
\[
\begin{eqnarray}
I_{2} &=& 3 \ \mathrm {[A]} \\[ 5pt ]
R &=& 4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
(b)の条件の時,各値を代入すると,
\[
\begin{eqnarray}
\begin{bmatrix} 12 \\ 8 \end{bmatrix} &=& \begin{bmatrix} 6 & 4 \\ 4 & 5 \end{bmatrix}\begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「2.逆行列\( \ \boldsymbol A^{-1} \ \)」により,両辺の左側から逆行列を掛けると,
\[
\begin{eqnarray}
\begin{bmatrix} 6 & 4 \\ 4 & 5 \end{bmatrix}^{-1}\begin{bmatrix} 12 \\ 8 \end{bmatrix} &=& \begin{bmatrix} 6 & 4 \\ 4 & 5 \end{bmatrix}^{-1}\begin{bmatrix} 6 & 4 \\ 4 & 5 \end{bmatrix}\begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} \\[ 5pt ]
\frac {1}{6\times 5-4\times 4}\begin{bmatrix} 5 & -4 \\ -4 & 6 \end{bmatrix}\begin{bmatrix} 12 \\ 8 \end{bmatrix} &=& \begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} \\[ 5pt ]
\begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} &=& \frac {1}{14}\begin{bmatrix} 28 \\ 0 \end{bmatrix} \\[ 5pt ]
&=& \begin{bmatrix} 2 \\ 0 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:リ
(c)の条件の時,各値を代入すると,
\[
\begin{eqnarray}
\begin{bmatrix} 12 \\ E_{2} \end{bmatrix} &=& \begin{bmatrix} 6 & 4 \\ 4 & 5 \end{bmatrix}\begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
すなわち,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
12 &=& 6I_{1}+4I_{2} &・・・・・・・①& \\[ 5pt ]
E_{2} &=& 4I_{1}+5I_{2} &・・・・・・・②& \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
となり,題意より\( \ I_{1}+I_{2}=1 ・・・・・・・③ \ \)となるので,①,③を解くと,
\[
\begin{eqnarray}
I_{1} &=& 4 \ \mathrm {[A]} \\[ 5pt ]
I_{2} &=& -3 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを②に代入すると,
\[
\begin{eqnarray}
E_{2} &=& 4I_{1}+5I_{2} \\[ 5pt ]
&=& 4\times 4+5\times (-3) \\[ 5pt ]
&=& 1 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん