【問題】
【難易度】★★★☆☆(普通)
次の文章は,分布定数回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は図を解答群の中から選びなさい。
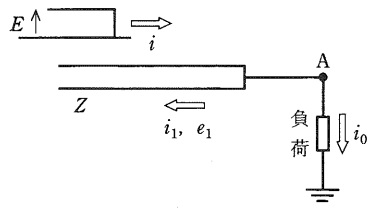
図のように特性インピーダンスが\( \ Z \ \)の半無限長無損失線路の終端\( \ \mathrm {A} \ \)に負荷が接続されている。
波頭が階段状で波高値\( \ E \ \)の電圧波\( \ e \ \)が\( \ Z \ \)側から終端\( \ \mathrm {A} \ \)に向かって入射し,それに伴い波頭が階段状で波高値\( \ I \ \)の電流\( \ i \ \)が流れた。入射波は時刻\( \ t=0 \ \)のとき終端\( \ \mathrm {A} \ \)に達した。このときの終端\( \ \mathrm {A} \ \)での電流\( \ i \ \)と反射による電流\( \ i_{1} \ \)及び負荷に流れる電流\( \ i_{0} \ \)との関係を求めたい。電流\( \ i_{1} \ \),電流\( \ i_{0} \ \)及び終端\( \ \mathrm {A} \ \)での反射により生じる電圧\( \ e_{1} \ \)を図のようにとる。電流は入射波が終端\( \ \mathrm {A} \ \)に向かって進行する方向を正とする。
負荷が静電容量\( \ C \ \)のときについて考える。\( \ C \ \)の電荷を\( \ q \ \)とする。ただし,時刻\( \ t=0 \ \)において\( \ q=0 \ \)とする。
入射波到達後において,終端\( \ \mathrm {A} \ \)での電圧,電流の関係は次式で表される。
\[
\begin{eqnarray}
&\left.
\begin{array}{l}
E+e_{1}=ZI+\left( -Zi_{1}\right) = \ \fbox { (1) } \ \\[ 5pt ]
I+i_{1}=i_{0} \\[ 5pt ]
\displaystyle i_{0}=\frac {\mathrm {d}q}{\mathrm {d}t}
\end{array}
\right\} \ ・・・・・・・・・・ ①
\end{eqnarray}
\]
これらの式より,\( \ q \ \)の時間変化を表す微分方程式が得られる。この式を初期値を考慮して解くと,
\[
\begin{eqnarray}
q&=& \ \fbox { (2) } \ \ ・・・・・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ i_{1} \ \)を\( \ I \ \)を用いて表すと次式となる。
\[
\begin{eqnarray}
i_{1}&=& \ \fbox { (3) } \ ・・・・・・・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
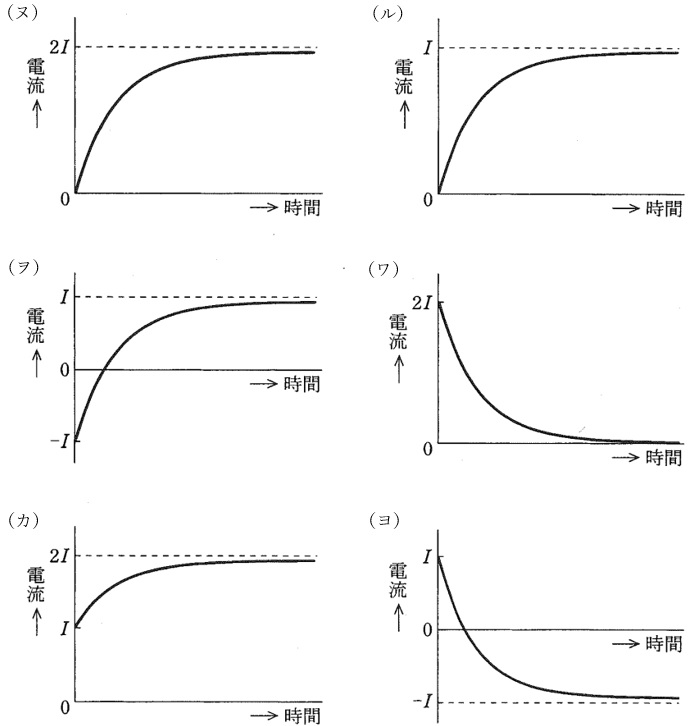
このときの\( \ i_{1} \ \)の時間的変化を表す図は\( \ \fbox { (4) } \ \)である。また,負荷に流れる電流\( \ i_{0} \ \)の時間的変化を表す図は\( \ \fbox { (5) } \ \)である。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& ZIC\left( 1-\mathrm {e}^{-\frac {1}{ZC}t}\right) &(ロ)& \frac {q}{C} &(ハ)& \left( 1-\mathrm {e}^{-\frac {1}{ZC}t}\right) I \\[ 5pt ]
&(ニ)& \frac {1}{C}\int q\mathrm {d}t &(ホ)& \left( \mathrm {e}^{-\frac {1}{ZC}t}-1\right) I &(ヘ)& 2ZIC\left( 1-\mathrm {e}^{-\frac {1}{ZC}t}\right) \\[ 5pt ]
&(ト)& \left( 2\mathrm {e}^{-\frac {1}{ZC}t}-1\right) I &(チ)& ZIC\left( \mathrm {e}^{-\frac {1}{ZC}t}-1\right) &(リ)& C\frac {\mathrm {d}q}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
分布定数回路における過渡現象を検討する問題です。
どちらかというと電力科目で出題されやすい分布定数回路と過渡現象を組み合わせた\( \ 1 \ \)種らしい問題と言えます。
\( \ 2 \ \)種のバックグラウンドがあり過渡現象の基本に忠実に解けば,十分に完答を目指せる問題かと思います。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ V_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ V_{\mathrm{L}} \ \),コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left ( \ln {x} \right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
4.分布定数回路における接続点での関係式
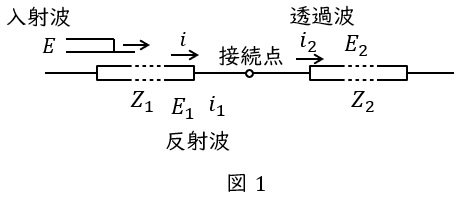
図1のような,特性インピーダンスが\( \ Z_{1} \ \)及び\( \ Z_{2} \ \)の非常に長い無損失線路が接続されているときの接続点での関係式を考えます。
図の左側から波高値\( \ E \ \)の電圧波が進入すると,接続点で一部の電圧が反射し,残りの電圧が透過します。このとき,入射波による電流を\( \ i \ \),反射波により生じる電圧及び電流を\( \ E_{1} \ \)及び\( \ i_{1} \ \),透過波により生じる電圧及び電流を\( \ E_{2} \ \)及び\( \ i_{2} \ \)とし,いずれの電流も右向きに流れる電流を正とすると,以下の電圧と電流の関係式が成り立ちます。
\[
\begin{eqnarray}
E +E_{1}&=&E_{2} \\[ 5pt ]
i +i_{1}&=&i_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,各電圧と電流には,
\[
\begin{eqnarray}
E&=&Z_{1}i \\[ 5pt ]
E_{1}&=&-Z_{1}i_{1} \\[ 5pt ]
E_{2}&=&Z_{2}i_{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立します。
※ 右向きを正とするので,電流\( \ i_{1} \ \)が負の値になることに注意しましょう。
【解答】
(1)解答:ロ
負荷の電圧を\( \ e_{2} \ \)とすると,終端\( \ \mathrm {A} \ \)での電圧の関係は,ワンポイント解説「4.分布定数回路における接続点での関係式」の通り,
\[
\begin{eqnarray}
E+e_{1}&=&ZI+\left( -Zi_{1}\right) = e_{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,負荷が静電容量\( \ C \ \)であるため,
\[
\begin{eqnarray}
e_{2}&=&\frac {q}{C} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヘ
(1)解答式より,
\[
\begin{eqnarray}
ZI+\left( -Zi_{1}\right) &=&\frac {q}{C} \\[ 5pt ]
I-i_{1}&=&\frac {q}{ZC} \\[ 5pt ]
i_{1}&=&I-\frac {q}{ZC} \\[ 5pt ]
\end{eqnarray}
\]
であり,これと①式の\( \ \displaystyle i_{0}=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)を①式の\( \ I+i_{1}=i_{0} \ \)に代入すると,
\[
\begin{eqnarray}
I+I-\frac {q}{ZC} &=&\frac {\mathrm {d}q}{\mathrm {d}t} \\[ 5pt ]
\frac {\mathrm {d}q}{\mathrm {d}t}+\frac {q}{ZC}&=&2I \\[ 5pt ]
\end{eqnarray}
\]
と\( \ q \ \)の微分方程式が導かれる。この微分方程式の定常解を\( \ q_{\mathrm {s}} \ \)とすると,ワンポイント解説「2.過渡現象における定常解と過渡解」の通り\( \ \displaystyle \frac {\mathrm {d}q}{\mathrm {d}t}=0 \ \)とすれば,
\[
\begin{eqnarray}
\frac {q_{\mathrm {s}}}{ZC}&=&2I \\[ 5pt ]
q_{\mathrm {s}}&=&2ZIC \\[ 5pt ]
\end{eqnarray}
\]
となり,過渡解を\( \ q_{\mathrm {t}} \ \)とすると,ワンポイント解説「2.過渡現象における定常解と過渡解」の通り微分方程式の右辺を零とすれば,
\[
\begin{eqnarray}
\frac {\mathrm {d}q_{\mathrm {t}}}{\mathrm {d}t}+\frac {q_{\mathrm {t}}}{ZC}&=&0 \\[ 5pt ]
\frac {\mathrm {d}q_{\mathrm {t}}}{\mathrm {d}t}&=&-\frac {q_{\mathrm {t}}}{ZC} \\[ 5pt ]
\frac {1}{q_{\mathrm {t}}}\mathrm {d}q_{\mathrm {t}}&=&-\frac {1}{ZC}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺積分すれば,
\[
\begin{eqnarray}
\int \frac {1}{q_{\mathrm {t}}}\mathrm {d}q_{\mathrm {t}}&=&\int -\frac {1}{ZC}\mathrm {d}t \\[ 5pt ]
\ln q_{\mathrm {t}}&=&-\frac {1}{ZC}t+C \left( C \ は積分定数\right) \\[ 5pt ]
q_{\mathrm {t}}&=&A\mathrm {e}^{-\frac {1}{ZC}t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,一般解\( \ q \ \)は,
\[
\begin{eqnarray}
q&=&q_{\mathrm {s}}+q_{\mathrm {t}} \\[ 5pt ]
&=&2ZIC+A\mathrm {e}^{-\frac {1}{ZC}t} \\[ 5pt ]
\end{eqnarray}
\]
となる。時刻\( \ t=0 \ \)における\( \ q=0 \ \)の関係より,
\[
\begin{eqnarray}
0&=&2ZIC+A \\[ 5pt ]
A&=&-2ZIC \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
q&=&2ZIC-2ZIC\mathrm {e}^{-\frac {1}{ZC}t} \\[ 5pt ]
&=&2ZIC\left( 1-\mathrm {e}^{-\frac {1}{ZC}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
①式の\( \ \displaystyle i_{0}=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)に(2)解答式を代入すると,
\[
\begin{eqnarray}
i_{0}&=&\frac {\mathrm {d}}{\mathrm {d}t}\left\{ 2ZIC\left( 1-\mathrm {e}^{-\frac {1}{ZC}t}\right)\right\} \\[ 5pt ]
&=&2ZIC\frac {\mathrm {d}}{\mathrm {d}t} \left( 1-\mathrm {e}^{-\frac {1}{ZC}t}\right) \\[ 5pt ]
&=&2ZIC\left\{ 0 -\left( -\frac {1}{ZC}\right)\mathrm {e}^{-\frac {1}{ZC}t}\right\} \\[ 5pt ]
&=&2I\mathrm {e}^{-\frac {1}{ZC}t} ・・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
となり,これを①式の\( \ I+i_{1}=i_{0} \ \)に代入すると,
\[
\begin{eqnarray}
I+i_{1}&=&2I\mathrm {e}^{-\frac {1}{ZC}t} \\[ 5pt ]
i_{1}&=&2I\mathrm {e}^{-\frac {1}{ZC}t}-I \\[ 5pt ]
&=&\left( 2\mathrm {e}^{-\frac {1}{ZC}t}-1\right) I \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
(3)解答式において,
\[
\begin{eqnarray}
i_{1}\left( 0\right) &=&\left( 2\mathrm {e}^{-\frac {1}{ZC}\times 0}-1\right) I \\[ 5pt ]
&=&I \\[ 5pt ]
i_{1}\left( \infty \right) &=&\left( 2\mathrm {e}^{-\frac {1}{ZC}\times \infty }-1\right) I \\[ 5pt ]
&=&-I \\[ 5pt ]
\end{eqnarray}
\]
であるから,条件を満たす図は(ヨ)と求められる。
(5)解答:ワ
④式において,
\[
\begin{eqnarray}
i_{0}\left( 0\right) &=&2I\mathrm {e}^{-\frac {1}{ZC}\times 0} \\[ 5pt ]
&=&2I \\[ 5pt ]
i_{0}\left( \infty \right) &=&2I\mathrm {e}^{-\frac {1}{ZC}\times \infty } \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
であるから,条件を満たす図は(ワ)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん