【問題】
【難易度】★★★☆☆(普通)
次の文章は,相互インダクタンスに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
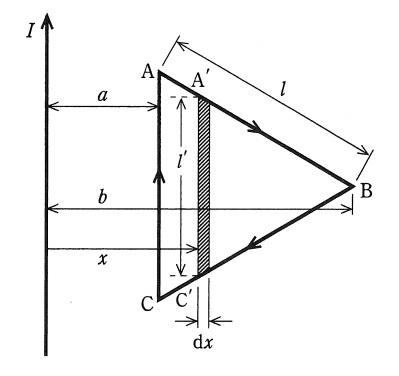
図のような,直線状の無限長導体に流れる電流と正三角形状の導体\( \ \mathrm {ABC} \ \)に流れる電流を考える。ここで,辺\( \ \mathrm {AC} \ \)は無限長導体と平行で,無限長導体との距離を\( \ a \ \),頂点\( \ \mathrm {B} \ \)の無限長導体との距離を\( \ b \ \),正三角形の一辺の長さを\( \ l \ \)とする。このとき,二つの導体間の相互インダクタンスを求めたい。なお,無限長導体と正三角形状の導体\( \ \mathrm {ABC} \ \)は同一平面上に存在し,導体の太さは無視できるものとする。
三角形\( \ \mathrm {ABC} \ \)は正三角形で,辺\( \ \mathrm {AC} \ \)は無限長導体と平行であるから,\( \ b \ \)を\( \ a \ \)及び\( \ l \ \)で表すと,次式となる。
\[
\begin{eqnarray}
b &=& \ \fbox { (1) } \ \\[ 5pt ]
\end{eqnarray}
\]
また,辺\( \ \mathrm {AB} \ \)及び辺\( \ \mathrm {BC} \ \)上に,無限長導体から距離\( \ x \ \)(\( \ a≦x≦b \ \))の位置の点\( \ \mathrm {A^{\prime }} \ \)及び\( \ \mathrm {C^{\prime }} \ \)を考えると,線分\( \ \mathrm {A^{\prime }C^{\prime }} \ \)の長さ\( \ l^{\prime } \ \)は,次式で表される。
\[
\begin{eqnarray}
l^{\prime } &=& \ \fbox { (2) } \ \\[ 5pt ]
\end{eqnarray}
\]
これより,無限長導体に流れる電流\( \ I \ \)による磁束のうち,図中の斜線部分(長さ\( \ l^{\prime } \ \), 幅\( \ \mathrm {d}x \ \))に鎖交する磁束\( \ \mathrm {d}\mathit {\Phi} \ \)は次式で表される。ここで,空間の透磁率を\( \ {\mu _{0}} \ \)とする。
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi} &=&\frac {\mu _{0}I}{2\pi }\left( \fbox { (3) } \right) \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
これを\( \ x \ \)について\( \ a \ \)から\( \ b \ \)まで積分することで,無限長導体に流れる電流がつくる磁束のうち,正三角形\( \ \mathrm {ABC} \ \)の内部に鎖交する磁束\( \ \mathit {\Phi} \ \)は次式で与えられる。
\[
\begin{eqnarray}
\mathit {\Phi} =\int ^{b}_{a}\frac {\mu _{0}I}{2\pi }\left( \fbox { (3) } \right) \mathrm {d}x=\frac {\mu _{0}I}{2\pi }\left( \fbox { (4) } \right) \\[ 5pt ]
\end{eqnarray}
\]
相互インダクタンス\( \ M \ \)は,\( \ \mathit {\Phi} \ \)と\( \ I \ \)を用いた定義式
\[
\begin{eqnarray}
M &=& \fbox { (5) } \\[ 5pt ]
\end{eqnarray}
\]
より,求めることができる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \left( l+\frac {2}{\sqrt {3}}a\right) \ln \left( 1+\frac {\sqrt {3}l}{2a}\right) -l &(ロ)& \frac {2}{\sqrt {3}}-\frac {2a}{\sqrt {3}x} &(ハ)& \frac {1}{x^{2}}\left( l-\frac {2}{\sqrt {3}}x+\frac {2}{\sqrt {3}}a\right) \\[ 5pt ]
&(ニ)& \frac {\sqrt {3}l}{2}\left( l+\frac {2}{\sqrt {3}}a-\frac {2}{\sqrt {3}}x\right) &(ホ)& a+\frac {\sqrt {3}}{2}l &(ヘ)& \frac {1}{x}\left( l+\frac {2}{\sqrt {3}}a\right) -\frac {2}{\sqrt {3}} \\[ 5pt ]
&(ト)& \frac {1}{2}\mathit {\Phi} I^{2} &(チ)& \frac {2}{\sqrt {3}}a+l &(リ)& \mathit {\Phi} I \\[ 5pt ]
&(ヌ)& l-\frac {2}{\sqrt {3}}\left( x-a\right) &(ル)& \frac {2}{\sqrt {3}}\left( x-a\right) &(ヲ)& a+\frac {1}{2}l \\[ 5pt ]
&(ワ)& \left( l+\frac {2}{\sqrt {3}}a\right) \ln \left( 1+\frac {\sqrt {3}l}{2a}\right) -\frac {l}{\sqrt {3}} &(カ)& \frac {\mathit {\Phi} }{I} &(ヨ)& \frac {al}{x}
\end{eqnarray}
\]
【ワンポイント解説】
アンペールの周回積分の法則,インダクタンス等電磁気学と自然対数の積分等数学の基本公式を組み合わせた問題です。
回路が正三角形であることで若干計算が複雑にはなりますが,類題も多いため一種の問題としては確実に得点しておきたい問題となります。
1.アンペア(アンペール)の周回積分の法則
空間上の磁界ベクトルを\( \ \boldsymbol H \ \),\( \ \mathrm {C} \ \)を閉曲線,\( \ \mathrm {d}\boldsymbol l \ \)を\( \ \mathrm {C} \ \)上の微小区間ベクトル,\( \ I \ \)を\( \ \mathrm {C} \ \)と鎖交する電流の総量とすると,
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,これをアンペアの周回積分の法則といいます。
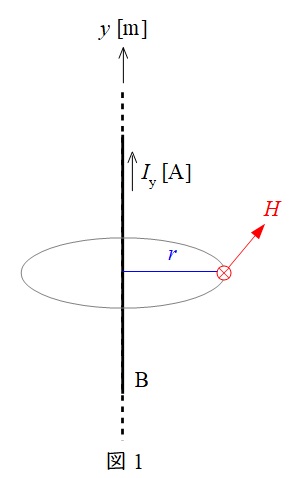
例えば,図1のように無限長直線電流\( \ I_{\mathrm {y}} \ \)が流れているとき,電線から距離\( \ r \ \)の位置での磁界の強さ\( \ H \ \)は,\( \ l=2\pi r \ \)なので,
\[
\begin{eqnarray}
2\pi r H&=&I_{\mathrm {y}} \\[ 5pt ]
H&=&\frac {I_{\mathrm {y}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ホ
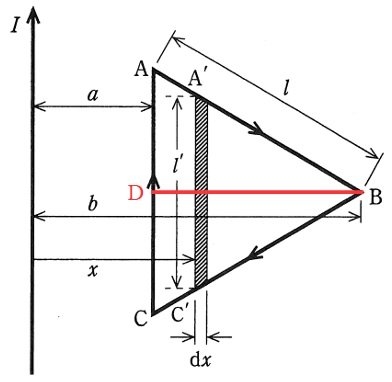
下図に示す通り、辺\( \ \mathrm {AC} \ \)に垂直に頂点\( \ \mathrm {B} \ \)から補助線\( \ \mathrm {BD} \ \)を引く。これより,
\[
\begin{eqnarray}
\mathrm {BD}&=&\frac {\sqrt {3}}{2}\mathrm {AB} \\[ 5pt ]
&=&\frac {\sqrt {3}}{2}l \\[ 5pt ]
\end{eqnarray}
\]
であるから、
\[
\begin{eqnarray}
b&=&a+\mathrm {BD} \\[ 5pt ]
&=&a+\frac {\sqrt {3}}{2}l \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヌ
下図に示す通り、\( \ \mathrm {BD} \ \)と\( \ \mathrm {A^{\prime }C^{\prime }} \ \)の交点を\( \ \mathrm {D^{\prime }} \ \)とする。
三角形の相似の関係から、
\[
\begin{eqnarray}
\frac {\mathrm {A^{\prime }C^{\prime }}}{\mathrm {AC}}&=&\frac {\mathrm {BD^{\prime }}}{\mathrm {BD}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\frac {l^{\prime }}{l}&=&\frac {b-x}{b-a} \\[ 5pt ]
&=&\frac {\displaystyle a+\frac {\sqrt {3}}{2}l-x}{\displaystyle a+\frac {\sqrt {3}}{2}l-a} \\[ 5pt ]
&=&\frac {\displaystyle a+\frac {\sqrt {3}}{2}l-x}{\displaystyle \frac {\sqrt {3}}{2}l} \\[ 5pt ]
\end{eqnarray}
\]
となる。これを\( \ l^{\prime } \ \)について整理すると,
\[
\begin{eqnarray}
l^{\prime }&=&\frac {\displaystyle a+\frac {\sqrt {3}}{2}l-x}{\displaystyle \frac {\sqrt {3}}{2}l}\cdot l \\[ 5pt ]
&=&\frac {2}{\sqrt {3}}\left( a+\frac {\sqrt {3}}{2}l-x \right) \\[ 5pt ]
&=&l+\frac {2}{\sqrt {3}}\left( a-x\right) \\[ 5pt ]
&=&l-\frac {2}{\sqrt {3}}\left( x-a\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(3)解答:ヘ
\( \ \mathrm {A^{\prime }C^{\prime }} \ \)上の磁界の強さ\( \ H \ \)は,ワンポイント解説「1.アンペア(アンペール)の周回積分の法則」から,
\[
\begin{eqnarray}
H&=&\frac {I}{2\pi x} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ \mathrm {A^{\prime }C^{\prime }} \ \)上の磁束密度\( \ B \ \)の大きさは,
\[
\begin{eqnarray}
B&=&\mu _{0}H \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi x} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって、微小区間\( \ \mathrm {d}S \ \)を鎖交する磁束\( \ \mathrm {d}\mathit {\Phi} \ \)は,
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi} &=&B\mathrm {d}S \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi x}l^{\prime }\mathrm {d}x \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi x}\left\{ l-\frac {2}{\sqrt {3}}\left( x-a\right) \right\} \mathrm {d}x \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi }\left\{ \frac {1}{x}\left( l+\frac {2}{\sqrt {3}}a\right) -\frac {2}{\sqrt {3}}\right\} \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※微小区間\( \ \mathrm {d}S \ \)は長さ\( \ l^{\prime } \ \)と\( \ \mathrm {d}x \ \)の長方形として近似します。
(4)解答:イ
(3)の解答式の両辺を積分すると,
\[
\begin{eqnarray}
\int ^{b}_{a}\frac {\mu _{0}I}{2\pi }\left\{ \frac {1}{x}\left( l+\frac {2}{\sqrt {3}}a\right) -\frac {2}{\sqrt {3}}\right\} \mathrm {d}x&=&\frac {\mu _{0}I}{2\pi }\left[ \left( l+\frac {2}{\sqrt {3}}a\right) \ln x-\frac {2}{\sqrt {3}}x\right] ^{b}_{a} \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi }\left\{ \left( l+\frac {2}{\sqrt {3}}a\right) \ln b-\frac {2}{\sqrt {3}}b\right\} -\left\{ \left( l+\frac {2}{\sqrt {3}}a\right) \ln a-\frac {2}{\sqrt {3}}a\right\} \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi }\left\{ \left( l+\frac {2}{\sqrt {3}}a\right) \ln \frac {b}{a}-\frac {2}{\sqrt {3}}\left( b-a\right) \right\} \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi }\left\{ \left( l+\frac {2}{\sqrt {3}}a\right) \ln \frac {a+\displaystyle \frac {\sqrt {3}}{2}l}{a}-\frac {2}{\sqrt {3}}\left( a+\frac {\sqrt {3}}{2}l-a\right) \right\} \\[ 5pt ]
&=&\frac {\mu _{0}I}{2\pi }\left\{ \left( l+\frac {2}{\sqrt {3}}a\right) \ln \left( 1+\frac {\sqrt {3}l}{2a}\right) -l\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
相互インダクタンスの定義より,
\[
\begin{eqnarray}
N\mathit {\Phi} &=&MI \\[ 5pt ]
\end{eqnarray}
\]
であり、\( \ N=1 \ \)であるから、
\[
\begin{eqnarray}
M&=&\frac {\mathit {\Phi}}{I} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん