【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,ベクトルポテンシャル,磁界及び電流に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
なお,ベクトルポテンシャルとは磁束密度\( \ \boldsymbol B \ \)に対して\( \ \boldsymbol B=\Delta \times \boldsymbol A \ \)を満たすベクトル\( \ \boldsymbol A \ \)のことであり,円筒座標系では,
\[
\begin{pmatrix} B_{\mathrm {r}} \\ B_{\theta } \\ B_{\mathrm {z}} \end{pmatrix}=\Delta \times \begin{pmatrix} A_{\mathrm {r}} \\ A_{\theta } \\ A_{\mathrm {z}} \end{pmatrix}=\begin{pmatrix} \displaystyle \frac {1}{r}\frac {\partial A_{z\mathrm {z}}}{\partial \theta }-\frac {\partial A_{\theta }}{\partial z } \\ \displaystyle \frac {\partial A_{\mathrm {r}}}{\partial z }-\frac {\partial A_{\mathrm {z}}}{\partial r } \\ \displaystyle \frac {1}{r}\frac {\partial \left( rA_{\theta }\right) }{\partial r }-\frac {1}{r}\frac {\partial A_{\mathrm {r}}}{\partial \theta } \end{pmatrix}
\]
と与えられる。
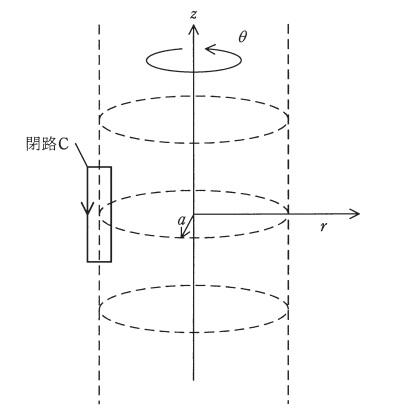
図のような円筒座標系において,以下の①式及び②式のように半径\(r\)の関数として定義されたベクトルポテンシャル\( \ \boldsymbol A \ \)を考える。なお,\( \ k \ \)は定数であり,\( \ \mu _{0} \ \)は真空の透磁率である。
\[
\begin{eqnarray}
A_{\mathrm {r}}\left( r,\theta , z \right) &=&A_{\mathrm {z}}\left( r,\theta , z \right) =0 &・・・・・・・・・・・・・・・①& \\[ 5pt ]
A_{\theta }\left( r,\theta , z \right)
&=&
\begin{cases}
\displaystyle kr & ( r ≦ a ) \\
\displaystyle \frac {ka^{2}}{r} & ( r > a )
\end{cases}
&・・・・・・・・・・・・・・・②&
\end{eqnarray}
\]
\( \ r < a \ \)における磁束密度は,
\[
B_{\mathrm {r}}=0,B_{\theta }=\fbox { (1) },B_{\mathrm {z}}=\fbox { (2) }
\]
\( \ r > a \ \)における磁束密度は,
\[
B_{\mathrm {r}}=0,B_{\theta }=\fbox { (1) },B_{\mathrm {z}}=\fbox { (1) }
\]
となる。
次に,このような磁界分布を形成する電流を考える。図中の閉路\( \ \mathrm {C} \ \)についてアンペールの法則を適用すると,電流は\( \ r=a \ \)の円筒面を\( \ \fbox { (3) } \ \)方向に流れていることになり,上記の分布は\( \ \fbox { (4) } \ \)に流れる電流が作り出す磁界を表していることが分かる。
\( \ z \ \)方向単位長さ当たりの電流密度が\( \ J \ \)である\( \ \fbox { (4) } \ \)に流れる電流の内部には磁束密度\( \ \mu _{0} J \ \)の一様な磁界が形成されることから,ベクトルポテンシャル\( \ \boldsymbol A \ \)は\( \ z \ \)方向単位長さ当たりの電流密度\( \ \fbox { (5) } \ \)の\( \ \fbox { (3) } \ \)方向電流によって形成されていることが分かる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {1}{k} &(ロ)& \theta &(ハ)& \frac {2k}{\mu _{0}} \\[ 5pt ]
&(ニ)& 直線状 &(ホ)& \mu _{0} k &(ヘ)& r \\[ 5pt ]
&(ト)& 2k &(チ)& k &(リ)& \frac {k}{r} \\[ 5pt ]
&(ヌ)& \frac {k}{r^{2}} &(ル)& 無限長直線状ソレノイド &(ヲ)& \frac {k}{2\pi \mu _{0}} \\[ 5pt ]
&(ワ)& 0 &(カ)& 円環状ソレノイド &(ヨ)& z
\end{eqnarray}
\]
【ワンポイント解説】
一見するとベクトルポテンシャルの難しい問題のようですが,中身は偏微分方程式への代入と,アンペールの法則の内容を問う問題で,特別難しい公式等は使用しません。
【解答】
(1)解答:ワ
(2)解答:ト
\( \ r ≦ a \ \)における磁束密度は,
\[
\begin{eqnarray}
B_{\mathrm {r}} &=& \frac {1}{r}\frac {\partial A_{\mathrm {z}}}{\partial \theta }-\frac {\partial A_{\theta }}{\partial z } \\[ 5pt ]
&=& 0-0 \\[ 5pt ]
&=& 0 \\[ 5pt ]
B_{\theta } &=& \frac {\partial A_{\mathrm {r}}}{\partial z }-\frac {\partial A_{\mathrm {z}}}{\partial r } \\[ 5pt ]
&=& 0-0 \\[ 5pt ]
&=& 0 \\[ 5pt ]
B_{\mathrm {z}} &=& \frac {1}{r}\frac {\partial \left( rA_{\theta }\right) }{\partial r }-\frac {1}{r}\frac {\partial A_{\mathrm {r}}}{\partial \theta } \\[ 5pt ]
&=& \frac {1}{r}\frac {\partial }{\partial r }\left( kr^{2}\right) -0 \\[ 5pt ]
&=& \frac {1}{r}\left( 2kr\right) \\[ 5pt ]
&=& 2k
\end{eqnarray}
\]
となり,\( \ r > a \ \)における磁束密度は,
\[
\begin{eqnarray}
B_{\mathrm {r}} &=& \frac {1}{r}\frac {\partial A_{\mathrm {z}}}{\partial \theta }-\frac {\partial A_{\theta }}{\partial z } \\[ 5pt ]
&=& 0-0 \\[ 5pt ]
&=& 0 \\[ 5pt ]
B_{\theta } &=& \frac {\partial A_{\mathrm {r}}}{\partial z }-\frac {\partial A_{\mathrm {z}}}{\partial r } \\[ 5pt ]
&=& 0-0 \\[ 5pt ]
&=& 0 \\[ 5pt ]
B_{\mathrm {z}} &=& \frac {1}{r}\frac {\partial \left( rA_{\theta }\right) }{\partial r }-\frac {1}{r}\frac {\partial A_{\mathrm {r}}}{\partial \theta } \\[ 5pt ]
&=& \frac {1}{r}\frac {\partial }{\partial r }\left( ka^{2}\right) -0 \\[ 5pt ]
&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
となる。
(3)解答:ロ
(4)解答:ル
(1),(2)より磁界は\( \ r < a \ \)の\( \ z \ \)方向のみに発生している。これは,円形コイルの電流により発生する中心磁界と同じである。よって,電流は図の\( \ \theta \ \)方向であり,この分布は無限長直線状ソレノイドに流れる電流が作り出す磁界を表している。
(5)解答:ハ
題意より\( \ B_{\mathrm {z}}=\mu _{0} J \ \)かつ(2)より\( \ B_{\mathrm {z}}=2k \ \)であるから,
\[
J=\frac {2k}{\mu _{0}}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん