《理論》〈電磁気〉[H24:問6]環状鉄心の磁気回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【用語の解説】
4 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，磁気回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

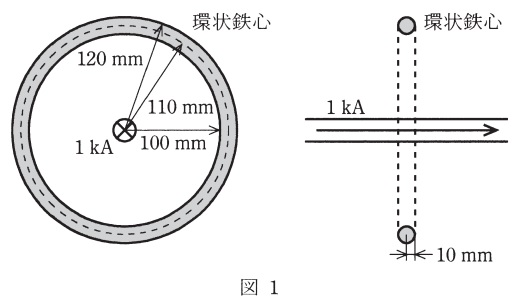
図1に示すように，断面が半径$ \ 10 \ \mathrm {[mm]} \ $の円形で，内半径が$ \ 100 \ \mathrm {[mm]} \ $，外半径が$ \ 120 \ \mathrm {[mm]} \ $の環状鉄心があり，中心に$ \ 1 \ \mathrm {[kA]} \ $の電流が流れているとする。真空の透磁率を$ \ \mu _{0}=4\pi \times 10^{-7} \ \mathrm {[H/m]} \ $，鉄の比透磁率を$ \ 800 \ $とするとき，環状鉄心中の磁束を求める。

環状鉄心の磁路長として，半径$ \ 110 \ \mathrm {[mm]} \ $の位置の円周の長さを考えると，環状鉄心の磁気抵抗$ \ R_{\mathrm {m}} \ $は$ \ \fbox {　（１）　} \ \mathrm {[A/Wb]} \ $である。よって，環状鉄心中の磁束$ \ \mathit {\Phi } \ $は$ \ \fbox {　（２）　} \ \mathrm {[Wb]} \ $と求まる。

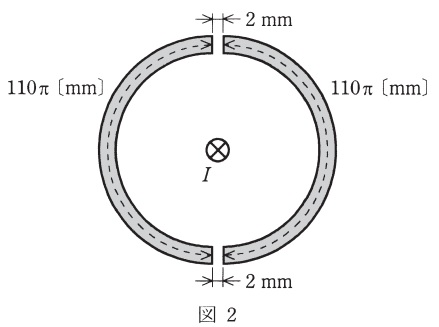
次に，図2に示すようにこの環状鉄心を平均磁路長が$ \ 110\pi \ \mathrm {[mm]} \ $の二つの鉄心に分割し，$ \ 2 \ \mathrm {[mm]} \ $の空げきを$ \ 2 \ $箇所設ける。空げきの磁路も，半径$ \ 10 \ \mathrm {[mm]} \ $の円形の断面を想定し，磁束の膨らみや漏れは考慮しない。これにより，中心を流れる電流が$ \ 1 \ \mathrm {[kA]} \ $のときの環状鉄心中の磁束密度$ \ B \ $は$ \ \fbox {　（３）　} \ \mathrm {[T]} \ $と求まる。

中心に流れる電流が増していくと，環状鉄心中の磁束密度はそれに比例して増加し，いずれ飽和する。環状鉄心の飽和磁束密度を$ \ 1.50 \ \mathrm {[T]} \ $とし，飽和磁束密度に達するまでは環状鉄心中の磁界は電流値に比例して増加していくとすると，中心を流れる電流$ \ I \ $が$ \ \fbox {　（４）　} \ \mathrm {[A]} \ $のときに環状鉄心中の磁束密度は飽和磁束密度に達する。

このような鉄心の空げき部に磁界を測定するセンサを配置することで電流を測定する方法が広く用いられている。例えば磁界センサとしては，$ \ \ \fbox {　（５）　} \ $効果により磁界を測定するものなどが実用化されている。

鉄心を用いず空心コイルを電流の周りに配置し，交流電流の電磁誘導による誘起電圧から電流波形を計測する$ \ \ \fbox {　（６）　} \ $コイルなども，磁界から電流を測定する方法として普及している。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　5.81\times 10^{3}　　　　　&（ロ）&　2.28\times 10^{-4}　　　　　&（ハ）&　2.75 \\[ 5pt ] &（ニ）&　2.58\times 10^{-1}　　　　　&（ホ）&　3.14\times 10^{-1}　　　　　&（ヘ）&　ペテルゼン \\[ 5pt ] &（ト）&　ペルチェ　　　　　&（チ）&　1.16\times 10^{4}　　　　　&（リ）&　4.52\times 10^{2} \\[ 5pt ] &（ヌ）&　ホール　　　　　&（ル）&　2.21　　　　　&（ヲ）&　ポッケルス \\[ 5pt ] &（ワ）&　1.45　　　　　&（カ）&　ヘルムホルツ　　　　　&（ヨ）&　2.19\times 10^{6} \\[ 5pt ] &（タ）&　4.77\times 10^{3}　　　　　&（レ）&　ロゴウスキー　　　　　&（ソ）&　4.57\times 10^{-4} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

磁気回路に関する問題と電気電子計測の問題を組み合わせたような問題です。
前半の(4)までは計算問題，(5)以降は知識確認の問題となっていますが，(6)以外の内容は比較的基本となる内容となっています。
計算間違いに注意して，確実に得点できるようにしましょう。

1.アンペールの周回積分の法則
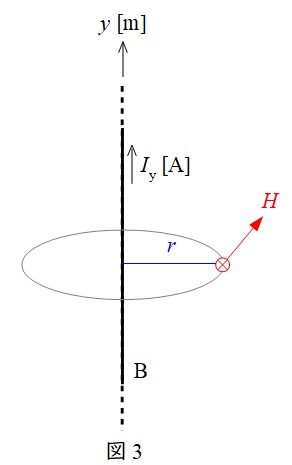
図3のように無限長直線電流$ \ I_{\mathrm {y}} \ $が流れているとき，電線から距離$ \ r \ $の位置での磁界の強さ$ \ H \ $は，
\[
\begin{eqnarray}
H&=&\frac {I_{\mathrm {y}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.磁気回路のオームの法則
中心長さ$ \ l \ $の環状鉄心に巻き数$ \ N \ $のコイルが巻かれ，そこに電流$ \ I \ $が流れている時，鉄心内の磁界の強さ$ \ H \ $は，アンペールの周回積分の法則より，
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ] H&=&\frac {NI}{l} \\[ 5pt ] \end{eqnarray}
\] であるから，鉄心内の磁束密度$ \ B \ $は，鉄心内の透磁率$ \ \mu \ $とすると，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] &=&\frac {\mu NI}{l} \\[ 5pt ] \end{eqnarray}
\] となります。鉄心内の磁束$ \ \phi \ $は，鉄心の断面積$ \ S \ $とすると，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ] \end{eqnarray}
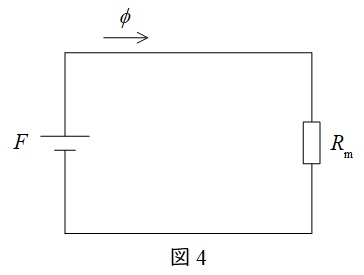
\] となり，起磁力$ \ F=NI \ $，磁気抵抗$ \ R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S} \ $とすると，
\[
\begin{eqnarray}
\phi &=&\frac {F}{R_{\mathrm {m}}} \\[ 5pt ] \end{eqnarray}
\] となり，磁気回路のオームの法則が成立します。

【用語の解説】

（ヘ）ペテルゼン
硝酸を利用して硫酸を製造する装置をペテルゼン硫酸製造装置といいます。

（ト）ペルチェ
異なる金属や半導体を接合して，電圧をかけると，吸熱もしくは発熱を発生する現象をペルチェ効果といいます。

（ヌ）ホール
半導体に電流を流し，電流に直角の磁界をかけたとき，電流と磁界に直角の方向に電圧が生じる現象をホール効果といいます。

（ヲ）ポッケルス
物質に電界をかけると，電界の強さに比例して屈折率が変化するという現象をポッケルス効果といいます。

（カ）ヘルムホルツ
空間に均一な磁界を発生させる装置をヘルムホルツコイルといいます。

（レ）ロゴウスキー　
導体を流れる電流を非接触で測定することが可能な鉄心を持たないコイルをロゴウスキーコイルといいます。

【解答】

(1)解答：ヨ
鉄心の磁路長$ \ l \ \mathrm {[m]} \ $は，鉄心の半径$ \ R=110\times 10^{-3} \ \mathrm {[m]} \ $であるから，
\[
\begin{eqnarray}
l &=&2\pi R \\[ 5pt ] &=&2\pi \times 110\times 10^{-3} \\[ 5pt ] &≒&0.69115 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] となり，断面積$ \ S \ \mathrm {[m^{2}]} \ $は半径$ \ r=10\times 10^{-3} \ \mathrm {[m]} \ $の円の断面であるから，
\[
\begin{eqnarray}
S &=&\pi r^{2} \\[ 5pt ] &=&\pi \times \left( 10\times 10^{-3}\right) ^{2} \\[ 5pt ] &≒&3.1416\times 10^{-4} \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] となる。真空の透磁率が$ \ \mu _{0}=4\pi \times 10^{-7} \ \mathrm {[H/m]} \ $，鉄の比透磁率が$ \ \mu _{\mathrm {r}}=800 \ $であるので，環状鉄心の磁気抵抗$ \ R_{\mathrm {m}} \ \mathrm {[A/Wb]} \ $は，
\[
\begin{eqnarray}
R_{\mathrm {m}} &=&\frac {l}{\mu _{\mathrm {r}}\mu_{0} S} \\[ 5pt ] &=&\frac {0.69115}{800\times 4\pi \times 10^{-7}\times 3.1416\times 10^{-4}} \\[ 5pt ] &≒&2.1884 \times 10^{6}　→　2.19 \times 10^{6} \ \mathrm {[A/Wb]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ソ
起磁力$ \ F \ \mathrm {[A]} \ $は巻き数$ \ 1 \ $と考えればよいので，
\[
\begin{eqnarray}
F &=&I \\[ 5pt ] &=&1.0 \times 10^{3} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるから，ワンポイント解説「2.磁気回路のオームの法則」の通り，環状鉄心中の磁束$ \ \mathit {\Phi } \ \mathrm {[Wb]} \ $は，
\[
\begin{eqnarray}
\mathit {\Phi } &=&\frac {F}{R_{\mathrm {m}}} \\[ 5pt ] &=&\frac {1.0 \times 10^{3}}{2.1884 \times 10^{6}} \\[ 5pt ] &≒&4.5695 \times 10^{-4}　→　4.57 \times 10^{-4} \ \mathrm {[Wb]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ニ
空げきの幅は$ \ \delta =2\times 10^{-3} \ \mathrm {[m]} \ $であるので，二つの空げき部の磁気抵抗の大きさ$ \ R_{\mathrm {m}}^{\prime } \ \mathrm {[A/Wb]} \ $は，
\[
\begin{eqnarray}
R_{\mathrm {m}}^{\prime } &=&\frac {2\delta }{\mu_{0} S} \\[ 5pt ] &=&\frac {2\times 2\times 10^{-3}}{4\pi \times 10^{-7}\times 3.1416\times 10^{-4}} \\[ 5pt ] &≒&1.0132 \times 10^{7}　\ \mathrm {[A/Wb]} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「2.磁気回路のオームの法則」の通り，環状鉄心中の磁束$ \ \mathit {\Phi }^{\prime } \ \mathrm {[Wb]} \ $は，
\[
\begin{eqnarray}
\mathit {\Phi }^{\prime } &=&\frac {F}{R_{\mathrm {m}}+R_{\mathrm {m}}^{\prime }} \\[ 5pt ] &=&\frac {1.0 \times 10^{3}}{2.1884 \times 10^{6}+1.0132 \times 10^{7}} \\[ 5pt ] &≒&8.1166\times 10^{-5} \ \mathrm {[Wb]} \\[ 5pt ] \end{eqnarray}
\] となり，磁束密度$ \ B \ \mathrm {[T]} \ $は，
\[
\begin{eqnarray}
B &=&\frac {\mathit {\Phi }^{\prime }}{S} \\[ 5pt ] &=&\frac {8.1166\times 10^{-5}}{3.1416\times 10^{-4}} \\[ 5pt ] &≒&0.25836　→　2.58 \times 10^{-1} \ \mathrm {[T]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：イ
題意より，電流と環状鉄心中の磁束密度は比例するので，飽和磁束密度$ \ B^{\prime }=1.50 \ \mathrm {[T]} \ $のときの電流を$ \ I^{\prime } \ \mathrm {[A]} \ $とすると，
\[
\begin{eqnarray}
\frac {I^{\prime }}{I} &=&\frac {B^{\prime }}{B} \\[ 5pt ] \frac {I^{\prime }}{1.0\times 10^{3}} &=&\frac {1.50}{0.25836} \\[ 5pt ] I^{\prime } &=&\frac {1.50}{0.25836}\times 1.0\times 10^{3} \\[ 5pt ] &≒&5.8058\times 10^{3}　→　5.81 \times 10^{3} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
用語の解説より，磁界を測定するための方法として最も適切なのはホール効果となります。

(6)解答：レ
用語の解説より，空心コイルを電流の周りに配置し，交流電流の電磁誘導による誘起電圧から電流波形を計測する方法として最も適切なのはロゴウスキーコイルとなります。
もう少し詳しく知りたい方はこちらを参照して下さい。