【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,誘電体が挿入された平行平板コンデンサに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
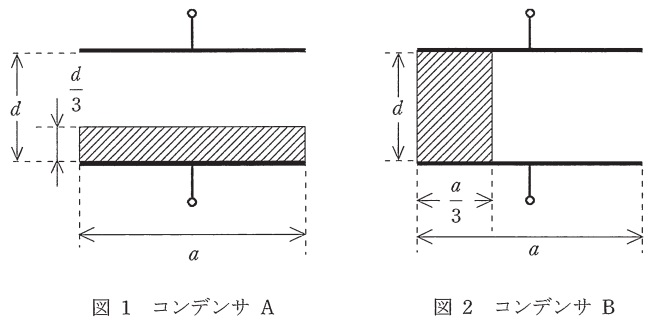
空気中に平行平板コンデンサがある。極板は一辺の長さが\( \ a \ \)の十分薄い正方形の導体平板であり,その極板間の距離は\( \ d \ \)である。なお,空気の誘電率を真空と同じ\( \ \varepsilon _{0} \ \)とし,端効果はないものとする。
このコンデンサに,図1のように,各辺が\( \ a \ \),\( \ a \ \),\( \ \displaystyle \frac {d}{3} \ \)の直方体で比誘電率が\( \ 4 \ \)の誘電体を,極板からはみ出さないように挿入したものをコンデンサ\( \ \mathrm {A} \ \)とする。
また,図2のように,コンデンサ\( \ \mathrm {A} \ \)の誘電体と同体積かつ同種の誘電体を使って,各辺が\( \ a \ \),\( \ \displaystyle \frac {a}{3} \ \),\( \ d \ \)の直方体の誘電体を極板からはみ出さないように挿入したものをコンデンサ\( \ \mathrm {B} \ \)とする。ただし,図1,2とも横から見た図である。
コンデンサ\( \ \mathrm {A} \ \)に電荷を与えたとき,誘電体中と空気中において\( \ \fbox { (1) } \ \)が等しくなる。また,コンデンサ\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)の静電容量は,それぞれ\( \ \fbox { (2) } \ \)と\( \ \fbox { (3) } \ \)である。
ここで,電界強度が\( \ E \ \)を超えると,使用した誘電体では絶縁破壊が起きるが,空気では絶縁破壊が起きないものとする。このとき,コンデンサ\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)の中の誘電体が絶縁破壊を起こさずに端子間に印加できる最大電圧は,それぞれ\( \ \fbox { (4) } \ \)と\( \ Ed \ \)である。したがって,各コンデンサに最大電圧を与えた際に蓄えられる静電エネルギーは,\( \ \fbox { (5) } \ \)。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {4\varepsilon _{0}a^{2}}{d} &(ロ)& \frac {4\varepsilon _{0}a^{2}}{3d} &(ハ)& \mathrm {B}の方が大きい \\[ 5pt ]
&(ニ)& Ed &(ホ)& 分 極 &(ヘ)& 電束密度 \\[ 5pt ]
&(ト)& 3Ed &(チ)& 同じである &(リ)& \frac {3\varepsilon _{0}a^{2}}{d} \\[ 5pt ]
&(ヌ)& \frac {2\varepsilon _{0}a^{2}}{d} &(ル)& \frac {6\varepsilon _{0}a^{2}}{5d} &(ヲ)& 4Ed \\[ 5pt ]
&(ワ)& 電 界 &(カ)& \frac {3\varepsilon _{0}a^{2}}{2d} &(ヨ)& \mathrm {A}の方が大きい
\end{eqnarray}
\]
【ワンポイント解説】
この問1は二種~三種レベルの問題となっているため,電験一種受験者にとってはかなり易しい問題と言えると思います。じっくりと考え,計算ミスがないようにしましょう。
1.電束密度\( \ \boldsymbol D \ \)と電界\( \ \boldsymbol E \ \)の関係
電束密度を\( \ \boldsymbol D \ \),誘電率を\( \ \varepsilon \ \),電界を\( \ \boldsymbol E \ \)とすると,
\[
\begin{eqnarray}
\boldsymbol D &=& \varepsilon \boldsymbol E \\[ 5pt ]
\end{eqnarray}
\]
となります。ただし,比誘電率を\( \ \varepsilon _{\mathrm {r}} \ \),真空の誘電率を\( \ \varepsilon _{0} \ \)とすると,
\[
\begin{eqnarray}
\varepsilon &=& \varepsilon _{\mathrm {r}}\varepsilon _{0} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間隔\( \ d \ \)とすると,
\[
\begin{eqnarray}
E &=& \frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.平行平板コンデンサの静電容量\( \ C \ \)
比誘電率\( \ \varepsilon _{\mathrm {r}} \ \),真空の誘電率\( \ \varepsilon _{0} \ \),極板間隔\( \ d \ \),極板面積\( \ S \ \)とすると,静電容量\( \ C \ \)は,
\[
\begin{eqnarray}
C &=& \frac {\varepsilon _{\mathrm {r}}\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.コンデンサの合成静電容量
静電容量\( \ C_{1} \ \)と\( \ C_{2} \ \)のコンデンサの合成静電容量\( \ C_{0} \ \)は,
並列接続時
\[
\begin{eqnarray}
C_{0} &=& C_{1}+C_{2} \\[ 5pt ]
\end{eqnarray}
\]
直列接続時
\[
\begin{eqnarray}
\frac {1}{C_{0}} &=& \frac {1}{C_{1}}+\frac {1}{C_{2}} ⇔ C_{0}=\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
5.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電容量を\( \ C \ \),コンデンサへの印加電圧\( \ V \ \)とすると,コンデンサに蓄えられる静電エネルギー\( \ W \ \)は,
\[
\begin{eqnarray}
W &=& \frac {1}{2}CV^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ヘ
コンデンサ\( \ \mathrm {A} \ \)において,端効果がないコンデンサにおいては,極板から出た電束はすべて反対側の極板へ吸収される。したがって,誘電体中も空気中も電束密度は等しくなる。
(2)解答:ロ
コンデンサ\( \ \mathrm {A} \ \)の空気中の静電容量\( \ C_{\mathrm {A1}} \ \)と誘電体の静電容量\( \ C_{\mathrm {A2}} \ \)は,ワンポイント解説「3.平行平板コンデンサの静電容量\( \ C \ \)」より,
\[
\begin{eqnarray}
C_{\mathrm {A1}} &=& \frac {\varepsilon _{0}a^{2}}{\displaystyle \frac {2}{3}d} \\[ 5pt ]
&=& \frac {3\varepsilon _{0}a^{2}}{2d} \\[ 5pt ]
C_{\mathrm {A2}} &=& \frac {\varepsilon _{\mathrm {r}}\varepsilon _{0}a^{2}}{\displaystyle \frac {d}{3}} \\[ 5pt ]
&=& \frac {4\varepsilon _{0}a^{2}}{\displaystyle \frac {d}{3}} \\[ 5pt ]
&=& \frac {12\varepsilon _{0}a^{2}}{d} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「4.コンデンサの合成静電容量」より,直列合成静電容量\( \ C_{\mathrm {A}} \ \)は,
\[
\begin{eqnarray}
C_{\mathrm {A}} &=& \frac {C_{\mathrm {A1}}C_{\mathrm {A2}}}{C_{\mathrm {A1}}+C_{\mathrm {A2}}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {3\varepsilon _{0}a^{2}}{2d}\cdot \frac {12\varepsilon _{0}a^{2}}{d}}{\displaystyle \frac {3\varepsilon _{0}a^{2}}{2d}+\frac {12\varepsilon _{0}a^{2}}{d}} \\[ 5pt ]
&=& \frac {4\varepsilon _{0}a^{2}}{3d} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヌ
(2)と同様に,コンデンサ\( \ \mathrm {B} \ \)の空気中の静電容量\( \ C_{\mathrm {B1}} \ \)と誘電体の静電容量\( \ C_{\mathrm {B2}} \ \)は,ワンポイント解説「3.平行平板コンデンサの静電容量\( \ C \ \)」より,
\[
\begin{eqnarray}
C_{\mathrm {B1}} &=& \frac {\displaystyle \varepsilon _{0}\frac {2}{3}a^{2}}{d} \\[ 5pt ]
&=& \frac {2\varepsilon _{0}a^{2}}{3d} \\[ 5pt ]
C_{\mathrm {B2}} &=& \frac {\displaystyle \varepsilon _{\mathrm {r}}\varepsilon _{0}\frac {a^{2}}{3}}{d} \\[ 5pt ]
&=& \frac {\displaystyle 4\varepsilon _{0}\frac {a^{2}}{3}}{d} \\[ 5pt ]
&=& \frac {4\varepsilon _{0}a^{2}}{3d} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「4.コンデンサの合成静電容量」より,並列合成静電容量\( \ C_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
C_{\mathrm {B}} &=& C_{\mathrm {B1}}+C_{\mathrm {B2}} \\[ 5pt ]
&=& \frac {2\varepsilon _{0}a^{2}}{3d}+\frac {4\varepsilon _{0}a^{2}}{3d} \\[ 5pt ]
&=& \frac {2\varepsilon _{0}a^{2}}{d} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ト
題意より,空気中では絶縁破壊が起きないので,コンデンサ\( \ \mathrm {A} \ \)が絶縁破壊を起こさずに印加できる電界強度の上限は,誘電体中の電界強度が\( \ E \ \)の時となる。コンデンサ中の電束密度\( \ D \ \)は等しいので,空気中の電界強度\( \ E_{1} \ \)と誘電体中の電界強度\( \ E_{2} \ \)は
\[
\begin{eqnarray}
E_{1} &=& \frac {D}{\varepsilon _{0}} \\[ 5pt ]
E_{2} &=& \frac {D}{\varepsilon _{\mathrm {r}}\varepsilon _{0}} \\[ 5pt ]
&=& \frac {D}{4\varepsilon _{0}}=E \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ E_{1}=4E_{2}=4E \ \)となる。
よって,コンデンサ\( \ \mathrm {A} \ \)が絶縁破壊を起こさずに端子間に印加できる最大電圧\( \ V_{\mathrm {A}} \ \)は,ワンポイント解説「2.電界\( \ E \ \)と電圧\( \ V \ \)の関係」より,
\[
\begin{eqnarray}
V_{\mathrm {A}} &=& E_{1}\cdot \frac {2}{3}d+E_{2}\cdot \frac {d}{3} \\[ 5pt ]
&=& 4E\cdot \frac {2}{3}d+E\cdot \frac {d}{3} \\[ 5pt ]
&=& 3Ed \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
それぞれのコンデンサに蓄えられる静電エネルギー\( \ W_{\mathrm {A}} \ \)及び\( \ W_{\mathrm {B}} \ \)は,ワンポイント解説「5.コンデンサの静電エネルギー\( \ W \ \)」より,
\[
\begin{eqnarray}
W_{\mathrm {A}} &=& \frac {1}{2}C_{\mathrm {A}}V_{\mathrm {A}}^{2} \\[ 5pt ]
&=& \frac {1}{2}\frac {4\varepsilon _{0}a^{2}}{3d}\left( 3Ed\right) ^{2} \\[ 5pt ]
&=& 6\varepsilon _{0}E^{2}a^{2}d \\[ 5pt ]
W_{\mathrm {B}} &=& \frac {1}{2}C_{\mathrm {B}}V_{\mathrm {B}}^{2} \\[ 5pt ]
&=& \frac {1}{2}\frac {2\varepsilon _{0}a^{2}}{d}\left( Ed\right) ^{2} \\[ 5pt ]
&=& \varepsilon _{0}E^{2}a^{2}d \\[ 5pt ]
\end{eqnarray}
\]
となり,蓄えられる静電エネルギーは,コンデンサ\( \ \mathrm {A} \ \)の方が大きくなる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん