《理論》〈電子理論〉[H29:問4] 半導体の電気伝導に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，半導体に光を照射した際に生じる電気伝導に関する記述である。文中の$\ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

長さ$\ L \ $の真性半導体試料に，上方から光を均一に照射したところ，場所によらず均一に，単位時間，単位体積当たり$\ g \ $個の電子－正孔対が生成した。ここで試料の厚さは十分薄く，光吸収に伴う厚さ方向の電子－正孔対密度の変化は無視できるものとする。
いま，熱平衡状態における試料の電子密度を$\ n_{0} \ $，正孔密度を$\ p_{0} \ $とし，光照射により生成した電子密度の増加分を$\ \Delta n \ $，正孔密度の増加分を$\ \Delta p \ $とするとき，$\ \Delta n \ $と$\ \Delta p \ $の大きさの関係を式で表すと，$\ \fbox {　 （１） 　} \ $である。光照射により，生成した電子のうち，単位時間，単位体積当たり$\ \displaystyle \frac {\Delta n}{\tau } \ $個が正孔と再結合して消滅する場合を考える。この$\ \tau \ $は再結合までの時間の目安であり，$\ \fbox {　 （２） 　} \ $と呼ばれる。定常状態では電子－正孔対の生成と消滅の割合は釣り合うことから，$\ \Delta n=\fbox {　 （３） 　} \ $となる。
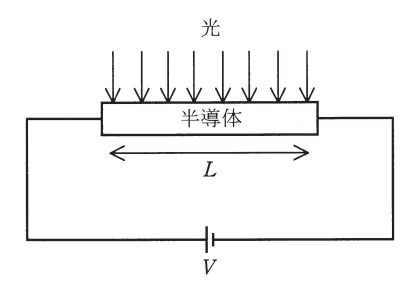
ここで図のように半導体試料の両端に電極を取り付け，電圧$\ V \ $を印加する。このとき，試料中には長さ方向に一様な電界$\ E=\fbox {　 （４） 　} \ $が発生し，電子と正孔は電界$\ E \ $からの力を受けて定常状態に達すると，$\ E \ $に比例したそれぞれ一定の平均速度で運動する。この比例定数を電子，正孔についてそれぞれ$\ \mu _{\mathrm {e}} \ $，$\ \mu _{\mathrm {h}} \ $とし，正孔の電荷量を$\ q \ $とすると，この運動による電流密度を計算することができる。光照射時の電流密度から，光を照射していないときの電流密度を差し引いて，光生成キャリアのみによる電流密度の大きさを求めると，$\ \fbox {　 （５） 　} \ $となる。これは，太陽電池や光検出器の基本原理として広く応用されている。

〔問4の解答群〕

$$\begin{eqnarray} &（イ）&　\frac {q\tau gV(\mu _{\mathrm {h}}-\mu _{\mathrm {e}})}{L}　　　&（ロ）&　キャリア寿命　　　&（ハ）&　\frac {g}{\tau } \\[ 5pt ] &（ニ）&　\Delta n\Delta p =n_{0}p_{0} 　　　&（ホ）&　\frac {V}{2L}　　　&（ヘ）&　\frac {V}{L} \\[ 5pt ] &（ト）&　緩和時間　　　&（チ）&　\Delta n\Delta p = (n_{0}+p_{0})\sqrt {n_{0}p_{0}}　　　&（リ）&　\frac {1}{\tau g} \\[ 5pt ] &（ヌ）&　\frac {2V}{L}　　　&（ル）&　\frac {q\tau gV(\mu _{\mathrm {h}}+\mu _{\mathrm {e}})}{L}　　　&（ヲ）&　回復時間 \\[ 5pt ] &（ワ）&　\Delta n =\Delta p　　　&（カ）&　\tau g　　　&（ヨ）&　\frac {q\tau gV(\mu _{\mathrm {h}}-\mu _{\mathrm {e}})}{2L} \end{eqnarray}$$

【ワンポイント解説】

問題自体はそれほど難解ではないのですが，あまり一種では出題されて来なかった分野なので，苦戦を強いられた受験生も多かったと思います。ただし，二種では過去に類題が出題されていたことがありますので，二種の過去問もカバーしていれば解ける問題かと思います。

1.電気伝導に関する公式
電界$\ E \ $が加わっている電界中に正孔と電子があるとすると，正孔は電界と同方向に，電子は電界と反対方向に動きます。その時の正孔と電子の速度を$\ v_{\mathrm {h}} \ $，$\ v_{\mathrm {e}} \ $，正孔と電子の移動度を$\ \mu _{\mathrm {h}} \ $，$\ \mu_{\mathrm {e}} \ $とすると，

$$\begin{eqnarray} v_{\mathrm {h}}&=&\mu _{\mathrm {h}}E \\[ 5pt ] v_{\mathrm {e}}&=&\mu _{\mathrm {e}}E \\[ 5pt ] \end{eqnarray}$$ となります。ここで，正孔の電荷量が$\ q \ $，電子の電荷量が$\ -q \ $で，正孔と電子の密度が$\ p \ $，$\ n \ $であるとすると，正孔と電子の電流密度$\ J_{\mathrm {h}} \ $，$J_{\mathrm {e}} \ $は，
$$\begin{eqnarray} J_{\mathrm {h}}&=&qpv_{\mathrm {h}}&=&qp\mu _{\mathrm {h}}E \\[ 5pt ] J_{\mathrm {e}}&=&-qnv_{\mathrm {e}}&=&-qn\mu _{\mathrm {e}}E \\[ 5pt ] \end{eqnarray}$$ となります。

【解答】

(1)解答：ワ
熱平衡状態における電子密度と正孔密度の増加分は等しいので，

$$\begin{eqnarray} \Delta n &=&\Delta p \\[ 5pt ] \end{eqnarray}$$ となる。

(2)解答：ロ
$\ \tau \ $は再結合までの時間の目安で，キャリア寿命を言います。

(3)解答：カ
定常状態において，電子－正孔対の生成量$\ g \ $と消滅量$\ \displaystyle \frac {\Delta n}{\tau} \ $は等しいので，

$$\begin{eqnarray} g&=&\frac {\Delta n}{\tau} \\[ 5pt ] \end{eqnarray}$$ となるから，
$$\begin{eqnarray} \Delta n &=&\tau g \\[ 5pt ] \end{eqnarray}$$ と求められる。

(4)解答：ヘ
長さ$\ L \ $の試料にて電圧$\ V \ $を印加した時の電界$\ E \ $は，

$$\begin{eqnarray} E&=&\frac {V}{L} \\[ 5pt ] \end{eqnarray}$$ となる。

(5)解答：ル
正孔と電子の光生成キャリアのみによる電流密度の大きさを$\ \Delta J_{\mathrm {h}} \ $，$\ \Delta J_{\mathrm {e}} \ $とすると，ワンポイント解説「1.電気伝導に関する公式」より，

$$\begin{eqnarray} \Delta J_{\mathrm {h}} &=& q\Delta p v_{\mathrm {h}} \\[ 5pt ] &=& q\Delta n\mu _{\mathrm {h}}E \\[ 5pt ] &=& q\tau g\mu _{\mathrm {h}}\frac {V}{L} \end{eqnarray}$$ $$\begin{eqnarray} \Delta J_{\mathrm {e}} &=& -q\Delta n v_{\mathrm {e}} \\[ 5pt ] &=& -q\tau g\mu _{\mathrm {e}}\frac {V}{L} \end{eqnarray}$$ となる。よって，電流密度の大きさ$\ \Delta J \ $は，
$$\begin{eqnarray} \Delta J &=& \Delta J_{\mathrm {h}}-\Delta J_{\mathrm {e}} \\[ 5pt ] &=& q\tau g\mu _{\mathrm {h}}\frac {V}{L}+q\tau g\mu _{\mathrm {e}}\frac {V}{L} \\[ 5pt ] &=& \frac {q\tau gV(\mu _{\mathrm {h}}+\mu _{\mathrm {e}})}{L} \\[ 5pt ] \end{eqnarray}$$ と求められる。