【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,円電流が作り出す磁束密度に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。なお,\( \ \mu _{0} \ \)は真空の透磁率である。
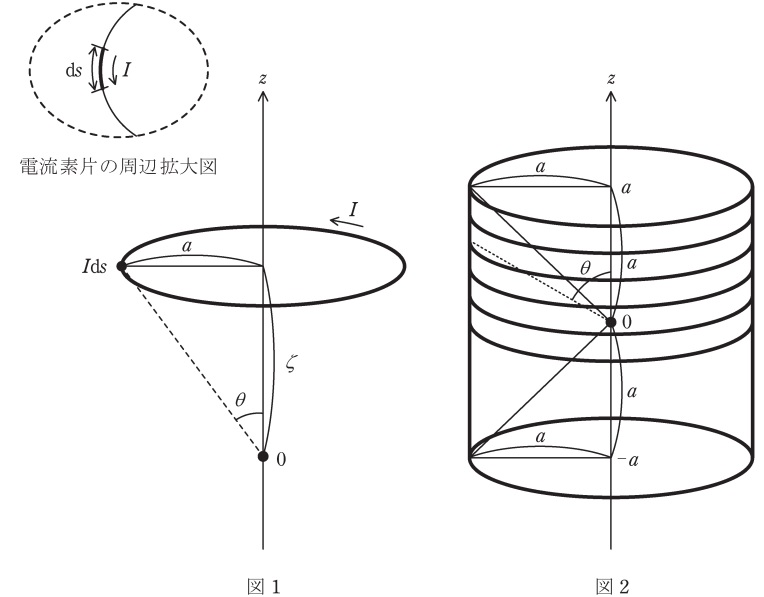
図1に示すように\( \ z \ \)軸を中心軸とし,\( \ z=\zeta \ \)の位置に中心を持つ半径\( \ a \ \)の円電流\( \ I \ \)が原点(\( \ z \ \)軸上の\( \ z=0 \ \)の点)に作る磁束密度をビオ・サバールの法則を用いて求める。円電流上の電流素片\( \ I\mathrm {d}s \ \)(\( \ \mathrm {d}s \ \)は円電流に沿った微小区間の長さ)と原点を結んだ直線と\( \ z \ \)軸とのなす角度を\( \ \theta \ \)とすると,\( \ \displaystyle \sin \theta =\frac {a}{\sqrt {a^{2}+\zeta ^{2}}} \ \)が成立することから,電流素片が原点に作る磁束密度の\( \ z \ \)方向の成分は\( \ \theta \ \)を用いて,
\[
\begin{eqnarray}
\mathrm {d}B_{\mathrm {z}} &=& \frac {\mu _{0}I}{4\pi }\frac {\sin ^{3}\theta }{a^{2}}\mathrm {d}s \\[ 5pt ]
\end{eqnarray}
\]
と表される。これを円周方向に線積分すると,円電流\( \ I \ \)が原点に作る磁束密度の\( \ z \ \)方向成分は,
\[
\begin{eqnarray}
B_{\mathrm {z}}(\theta ) &=& \fbox { (1) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。一方,原点における磁束密度の\( \ z \ \)軸に直交する成分は,対称性から
\[
\begin{eqnarray}
B_{\mathrm {⊥}}(\theta ) &=& \fbox { (2) } \\[ 5pt ]
\end{eqnarray}
\]
となる。
次に,図2に示すように\( \ z \ \)軸を中心軸とし,原点を中心とする半径\( \ a \ \),長さ\( \ 2a \ \)の有限長ソレノイドを考える。\( \ z=\zeta \ \)の位置に中心をもつ円電流\( \ I \ \)が原点に作る磁束密度の\( \ z \ \)方向成分を\( \ B_{\mathrm {z}}(\zeta ) \ \)と置くと,単位長さ当たりの巻き数\( \ n \ \)が十分に大きい場合には,ソレノイドに流れる電流\( \ I \ \)がソレノイドの中心に作る磁束密度は,
\[
\begin{eqnarray}
B_{1} &=&\int _{-a}^{a} nB_{\mathrm {z}}(\zeta ) \mathrm {d}\zeta \\[ 5pt ]
\end{eqnarray}
\]
と表される。いま,ソレノイド上の電流素片と原点を結んだ直線と\( \ z \ \)軸とのなす角度を\( \ \theta \ \)とすると,\( \ \displaystyle \zeta =\frac {a}{\tan \theta }\)の関係が成り立つので,\( \ \displaystyle \mathrm {d}\zeta =-\frac {a}{\sin ^{2}\theta }\mathrm {d}\theta \ \)を利用して変数変換すると,
\[
\begin{eqnarray}
B_{1} &=&\int _{3\pi /4}^{\pi /4} \fbox { (3) } \mathrm {d}\theta =\fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
となる。
同様に,無限長ソレノイドの軸上の磁束密度は,
\[
\begin{eqnarray}
B_{2} &=&\fbox { (5) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \mu _{0}I &(ロ)& \frac {\mu _{0}I}{2 }\frac {\sin ^{3}\theta }{a} &(ハ)& \frac {\mu _{0}nI}{2} \\[ 5pt ]
&(ニ)& 2\mu _{0}nI &(ホ)& \mu _{0}nI &(ヘ)& -\frac {\mu _{0}nI}{2}\sin \theta \\[ 5pt ]
&(ト)& \frac {\mu _{0}nI}{\sqrt {2}} &(チ)& -\frac {\mu _{0}nI}{2} &(リ)& 4\mu _{0}nI \\[ 5pt ]
&(ヌ)& \sqrt {2}\mu _{0}nI &(ル)& \frac {\mu _{0}I}{2 }\frac {\sin ^{2}\theta }{a} &(ヲ)& \frac {\mu _{0}I}{2a} \\[ 5pt ]
&(ワ)& 0 &(カ)& -\mu _{0}nI\frac {a}{\sin \theta } &(ヨ)& \mu _{0}I\sin \theta
\end{eqnarray}
\]
【ワンポイント解説】
電磁気の問題というよりも,積分の計算問題に近いような問題です。線積分を使用し,変数変換の積分を行うので,やや高度な数学を使用しますが,計算はそれほど複雑ではありませんので,一種受験生にとってはやや易しい問題であると思います。最終的に(5)の結果がアンペールの法則と一致することを確認できれば理想です。
1.ビオ・サバールの法則
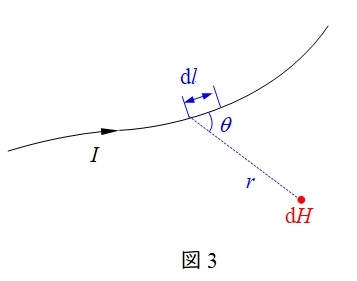
図3に示すように,微小な長さ\( \ \mathrm {d}l \ \)に流れる電流\( \ I \ \)が,距離\( \ r \ \)離れた場所に作る磁界\( \ \mathrm {d} H \ \)は,
\[
\begin{eqnarray}
\mathrm {d} H&=&\frac {I \mathrm {d}l}{4\pi r^{2}}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.磁束密度\( \ B \ \)と磁界\( \ H \ \)の関係
真空の透磁率を\( \ \mu _{0} \ \)とすると,磁束密度\( \ B \ \)と磁界\( \ H \ \)には,
\[
\begin{eqnarray}
B &=& \mu _{0}H \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(1)解答:ロ
円電流上の電流素片\( \ I\mathrm {d}s \ \)が原点に作る磁界の大きさ\( \ \mathrm {d}H \ \)は,ワンポイント解説「1.ビオ・サバールの法則」より,
\[
\begin{eqnarray}
\mathrm {d} H&=&\frac {I \mathrm {d}s}{4\pi \left( a^{2}+\zeta ^{2}\right) } \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \displaystyle \sin \theta =\frac {a}{\sqrt {a^{2}+\zeta ^{2}}} \ \)すなわち\( \ \displaystyle \sqrt {a^{2}+\zeta ^{2}}=\frac {a}{\sin \theta } \ \)であるから,
\[
\begin{eqnarray}
\mathrm {d} H&=&\frac {I \mathrm {d}s}{4\pi \left( a^{2}+\zeta ^{2}\right) } \\[ 5pt ]
&=&\frac {I \mathrm {d}s}{4\pi \left( \displaystyle \frac {a}{\sin \theta }\right) ^{2}} \\[ 5pt ]
&=& \frac {I}{4\pi }\frac {\sin ^{2}\theta }{a^{2}}\mathrm {d}s \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ワンポイント解説「2.磁束密度\( \ B \ \)と磁界\( \ H \ \)の関係」より,磁束密度\( \ \mathrm {d}B \ \)は,
\[
\begin{eqnarray}
\mathrm {d} B&=& \mu _{0}\mathrm {d} H \\[ 5pt ]
&=& \frac { \mu _{0}I}{4\pi }\frac {\sin ^{2}\theta }{a^{2}}\mathrm {d}s \\[ 5pt ]
\end{eqnarray}
\]
となり,その\( \ z \ \)方向の成分\( \ \mathrm {d}B_{\mathrm {z}} \ \)は,
\[
\begin{eqnarray}
\mathrm {d}B_{\mathrm {z}}&=&\mathrm {d} B\sin \theta \\[ 5pt ]
&=& \frac { \mu _{0}I}{4\pi }\frac {\sin ^{3}\theta }{a^{2}}\mathrm {d}s \\[ 5pt ]
\end{eqnarray}
\]
と求められる。これを円周方向に線積分すると,円周のすべての電流素片について同じ大きさの磁束密度となるので,
\[
\begin{eqnarray}
B_{\mathrm {z}}(\theta ) &=& \int _{0}^{2\pi a} \frac { \mu _{0}I}{4\pi }\frac {\sin ^{3}\theta }{a^{2}}\mathrm {d}s \\[ 5pt ]
&=& \frac { \mu _{0}I}{4\pi }\frac {\sin ^{3}\theta }{a^{2}} \int _{0}^{2\pi a} 1 \ \mathrm {d}s \\[ 5pt ]
&=& \frac { \mu _{0}I}{4\pi }\frac {\sin ^{3}\theta }{a^{2}} \times 2\pi a \\[ 5pt ]
&=& \frac {\mu _{0}I}{2 }\frac {\sin ^{3}\theta }{a} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
原点における磁束密度の\( \ z \ \)軸に直交する成分は,対称性により打ち消し合うので,
\[
\begin{eqnarray}
B_{\mathrm {⊥}}(\theta ) &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
となる。
(3)解答:ヘ
有限長ソレノイドについて,微小長さ\( \ \mathrm {d}\zeta \ \)の円電流が原点に作る磁束密度の大きさ\( \ \mathrm {d}B_{1} \ \)の\( \ z \ \)成分は,
\[
\begin{eqnarray}
\mathrm {d}B_{1} &=& nB_{\mathrm {z}}\mathrm {d}\zeta \\[ 5pt ]
\end{eqnarray}
\]
であり,有限長ソレノイドが\( \ -a \ \)から\( \ a \ \)までであるから,両辺積分すると,
\[
\begin{eqnarray}
B_{1} &=&\int _{-a}^{a} nB_{\mathrm {z}}(\zeta ) \mathrm {d}\zeta \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \displaystyle \zeta =\frac {a}{\tan \theta }\)の関係が成り立ち,\( \ \zeta =-a \ \)の時\( \ \displaystyle \theta = \frac {3\pi }{4} \ \),\( \ \zeta =a \ \)の時\( \ \displaystyle \theta = \frac {\pi }{4} \ \)である。\( \ \displaystyle \mathrm {d}\zeta =-\frac {a}{\sin ^{2}\theta }\mathrm {d}\theta \ \)を利用して変数変換すると,
\[
\begin{eqnarray}
B_{1} &=&\int _{-a}^{a} nB_{\mathrm {z}}(\zeta ) \mathrm {d}\zeta \\[ 5pt ]
&=&\int _{\frac {3\pi }{4}}^{\frac {\pi }{4}} nB_{\mathrm {z}}(\theta ) \times \left( -\frac {a}{\sin ^{2}\theta }\right) \mathrm {d}\theta \\[ 5pt ]
&=&\int _{\frac {3\pi }{4}}^{\frac {\pi }{4}} \frac {\mu _{0}nI}{2 }\frac {\sin ^{3}\theta }{a} \times \left( -\frac {a}{\sin ^{2}\theta }\right) \mathrm {d}\theta \\[ 5pt ]
&=&\int _{\frac {3\pi }{4}}^{\frac {\pi }{4}} -\frac {\mu _{0}nI}{2}\sin \theta \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ト
(3)の解答式を計算すると,
\[
\begin{eqnarray}
B_{1} &=&\int _{\frac {3\pi }{4}}^{\frac {\pi }{4}} -\frac {\mu _{0}nI}{2}\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\int _{\frac {3\pi }{4}}^{\frac {\pi }{4}} \sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\left[ -\cos \theta \right] _{\frac {3\pi }{4}}^{\frac {\pi }{4}} \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\left[ -\frac {1}{\sqrt {2}}-\frac {1}{\sqrt {2}} \right] \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\times \left( -\sqrt {2} \right) \\[ 5pt ]
&=&\frac {\mu _{0}nI}{\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ホ
無限長ソレノイドの磁束密度は(4)で\( \ \theta \ \)を\( \ \theta =\pi \ \)から\( \ \theta =0 \ \)まで積分したものであるから,
\[
\begin{eqnarray}
B_{1} &=&\int _{\pi }^{0} -\frac {\mu _{0}nI}{2}\sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\int _{\pi }^{0} \sin \theta \mathrm {d}\theta \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\left[ -\cos \theta \right] _{\pi }^{0} \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\left[ -1-1 \right] \\[ 5pt ]
&=&-\frac {\mu _{0}nI}{2}\times \left( -2 \right) \\[ 5pt ]
&=&\mu _{0}nI \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん