《理論》〈電磁気〉[H27:問2]直流遮断器の開放機構などに応用される磁気回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，直流遮断器の開放機構などに応用される磁気回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

図1は固定された鉄心$ \ \mathrm {B} \ $に鉄心$ \ \mathrm {A} \ $が吸着されている電磁石を示している。鉄心$ \ \mathrm {B} \ $には巻線$ \ 1 \ $及び巻線$ \ 2 \ $が巻かれており，直流電流$ \ I_{1} \ $及び$ \ I_{2} \ $で励磁されている。鉄心$ \ \mathrm {A} \ $にはばねの力が図の左方向に作用しており，電磁石の吸着力がばねのけん引力よりも弱まると，鉄心$ \ \mathrm {A} \ $が鉄心$ \ \mathrm {B} \ $から離れる仕組みとなっている。

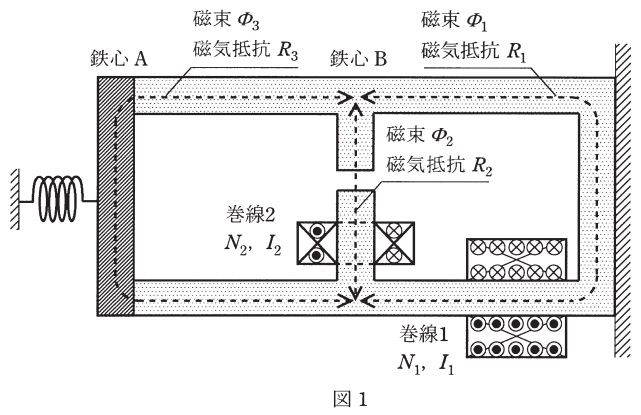
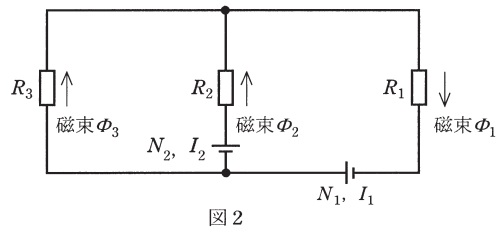
図1の電磁石を磁気回路で示したのが図2である。磁気抵抗$ \ R_{1} \ $は，鉄心$ \ \mathrm {B} \ $の右側部分の磁路の磁気抵抗で，断面積$ \ S \ $，長さ$ \ L \ $とすると，$ \ R_{1}= \ \fbox {　（１）　} \ $と表される。磁気抵抗$ \ R_{2} \ $は，鉄心$ \ \mathrm {B} \ $の中央部分の磁路の磁気抵抗で，断面積$ \ S \ $，長さ$ \ l \ $(空隙部分を含む)，空隙部分の長さを$ \ g \ $($ \ g ≪ l \ $)とすると，$ \ R_{2}= \ \fbox {　（２）　} \ $と表される。このとき，鉄心$ \ \mathrm {A} \ $，$ \ \mathrm {B} \ $の比透磁率を$ \ \mu _{\mathrm {r}} \ $，空気の透磁率を$ \ \mu _{0} \ $とする。

鉄心$ \ \mathrm {B} \ $の左側と鉄心$ \ \mathrm {A} \ $からなる部分のの磁路の磁気抵抗を$ \ R_{3} \ $とし，図2で示すように各部の磁束を$ \ \mathit {\Phi}_{1} \ $，$ \ \mathit {\Phi}_{2} \ $，$ \ \mathit {\Phi}_{3} \ $とするとき，以下の磁気回路の方程式が得られる。
\[
\begin{eqnarray}
\mathit {\Phi}_{1} &=& \mathit {\Phi}_{2}+\mathit {\Phi}_{3} &　・・・・・・・　①&\\[ 5pt ] N_{1}I_{1}&=& \fbox {　（３）　} &　・・・・・・・　②&\\[ 5pt ] N_{1}I_{1}+N_{2}I_{2}&=& R_{1}\mathit {\Phi}_{1} +R_{2}\mathit {\Phi}_{2}&　・・・・・・・　③&
\end{eqnarray}
\] このとき，①式～③式を用いて磁束$ \ \mathit {\Phi}_{3} \ $を求めると，磁気抵抗$ \ R_{1} \ $，$ \ R_{2} \ $，$ \ R_{3} \ $及び$ \ N_{1} \ $，$ \ N_{2} \ $，$ \ I_{1} \ $，$ \ I_{2} \ $を用いて磁束$ \ \mathit {\Phi}_{3} \ $は次式で表され，主回路電流$ \ I_{2} \ $が増すと磁束$ \ \mathit {\Phi}_{3} \ $が減少することが分かる。
\[
\mathit {\Phi}_{3}=\fbox {　（４）　}
\] 磁気抵抗$ \ R_{1} \ $，$ \ R_{2} \ $，$ \ R_{3} \ $をそれぞれ，$ \ R_{1}=R_{3}=2.0\times 10^{5} \ \mathrm {A/Wb} \ $，$ \ R_{2}=1.0\times 10^{7} \ \mathrm {A/Wb} \ $，巻線$ \ 1 \ $の巻数を$ \ N_{1}=500 \ $，電流を$ \ I_{1}=0.9 \ \mathrm {A} \ $，巻線$ \ 2 \ $の巻数を$ \ N_{2}=2 \ $とする。また，鉄心$ \ \mathrm {A} \ $の部分の磁束$ \ \mathit {\Phi}_{3} \ $が$ \ 0.5 \ \mathrm {mWb} \ $まで減少したとき，鉄心$ \ \mathrm {A} \ $が鉄心$ \ \mathrm {B} \ $から離れることとする。このとき，巻線$ \ 2 \ $を流れる主回路電流$ \ I_{2} \ $が$ \ \fbox {　（５）　} \ \mathrm {kA} \ $に達したときに直流遮断器を自動的に開放させる機構として，この電磁石を利用することができる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {R_{1}N_{1}I_{1}-R_{2}N_{2}I_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}　　　　　&（ロ）&　R_{1}\mathit {\Phi}_{1}+R_{2}\mathit {\Phi}_{2}　　　　　&（ハ）&　\frac {L}{\mu _{\mathrm {r}}\mu _{0}S} \\[ 5pt ] &（ニ）&　\frac {\mu _{\mathrm {r}}\mu _{0}S}{L}　　　　　&（ホ）&　\frac {R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_{2}N_{2}I_{2}-R_{1}N_{1}I_{1}}　　　　　&（ヘ）&　0.23 \\[ 5pt ] &（ト）&　\frac {\mu _{\mathrm {r}}\mu _{0}(l-g)}{S}+\frac {\mu _{0}g}{S}　　　　　&（チ）&　\frac {R_{2}N_{1}I_{1}-R_{1}N_{2}I_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}　　　　　&（リ）&　\frac {\mu _{\mathrm {r}}\mu _{0}L}{S} \\[ 5pt ] &（ヌ）&　\frac {l-g}{\mu _{\mathrm {r}}\mu _{0}S}+\frac {g}{\mu _{0}S}　　　　　&（ル）&　R_{1}\mathit {\Phi}_{1}+R_{3}\mathit {\Phi}_{3}　　　　　&（ヲ）&　6.2 \\[ 5pt ] &（ワ）&　\frac {g(l-g)}{\mu _{0}S(l-g)+\mu _{\mathrm {r}}\mu _{0}Sg}　　　　　&（カ）&　1.5　　　　　&（ヨ）&　R_{2}\mathit {\Phi}_{2}+R_{3}\mathit {\Phi}_{3}
\end{eqnarray}
\]

【ワンポイント解説】

磁気回路の問題で，基本的な公式を理解していれば難なく解けると思います。電験一種受験者であれば完答したい問題です。

1.磁気抵抗$ \ R_{\mathrm {m}} \ $
透磁率$ \ \mu \ $の回路において，断面積$ \ S \ $，長さ$ \ l \ $とすると，
\[
R_{\mathrm {m}}=\frac {l}{\mu S}
\] となります。

2.磁気回路のオームの法則
電気回路における起電力$ \ V \ $を起磁力$ \ NI \ $，電流$ \ I \ $を磁束$ \ \mathit {\Phi} \ $，抵抗$ \ R \ $を磁気抵抗$ \ R_{\mathrm {m}} \ $と置き換えれば，
\[
NI=R_{\mathrm {m}}\mathit {\Phi}
\] の関係が成立します。

【解答】

(1)解答：ハ
磁気回路内の透磁率$ \ \mu \ $は，
\[
\mu =\mu _{\mathrm {r}}\mu _{0}
\] であるから，ワンポイント解説「1.磁気抵抗$ \ R_{\mathrm {m}} \ $」より，右側部分の磁気抵抗$ \ R_{1} \ $は，
\[
\begin{eqnarray}
R_{1}&=&\frac {L}{\mu S} \\[ 5pt ] &=&\frac {L}{\mu _{\mathrm {r}}\mu _{0} S} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヌ
中央部分の鉄心の長さは$ \ l-g \ $であるから，磁気抵抗$ \ R_{2} \ $は，
\[
R_{2}=\frac {l-g}{\mu _{\mathrm {r}}\mu _{0} S}+\frac {g}{\mu _{0} S}
\] と求められる。

(3)解答：ル
左側と右側の磁気回路における回路方程式は，ワンポイント解説「2.磁気回路のオームの法則」より，
\[
N_{1}I_{1}=R_{1}\mathit {\Phi}_{1}+R_{3}\mathit {\Phi}_{3}
\] と求められる。

(4)解答：チ
①より，
\[
\mathit {\Phi}_{2} = \mathit {\Phi}_{1}-\mathit {\Phi}_{3} 　・・・・・・・　①^{\prime }
\] となるから，これを③に代入すると，
\[
\begin{eqnarray}
N_{1}I_{1}+N_{2}I_{2}&=& R_{1}\mathit {\Phi}_{1} +R_{2}\mathit {\Phi}_{2} \\[ 5pt ] N_{1}I_{1}+N_{2}I_{2}&=& R_{1}\mathit {\Phi}_{1} +R_{2}( \mathit {\Phi}_{1}-\mathit {\Phi}_{3} ) \\[ 5pt ] N_{1}I_{1}+N_{2}I_{2}&=& (R_{1} +R_{2}) \mathit {\Phi}_{1}-R_{2}\mathit {\Phi}_{3} \\[ 5pt ] (R_{1} +R_{2}) \mathit {\Phi}_{1}&=& N_{1}I_{1}+N_{2}I_{2}+R_{2}\mathit {\Phi}_{3} \\[ 5pt ] \mathit {\Phi}_{1}&=& \frac {1}{R_{1} +R_{2}}(N_{1}I_{1}+N_{2}I_{2}+R_{2}\mathit {\Phi}_{3}) \\[ 5pt ] \end{eqnarray}
\] となるので，これを②に代入すると，
\[
\begin{eqnarray}
N_{1}I_{1}&=& R_{1}\mathit {\Phi}_{1}+R_{3}\mathit {\Phi}_{3} \\[ 5pt ] N_{1}I_{1}&=& \frac {R_{1}}{R_{1} +R_{2}}(N_{1}I_{1}+N_{2}I_{2}+R_{2}\mathit {\Phi}_{3})+R_{3}\mathit {\Phi}_{3} \\[ 5pt ] \frac {R_{2}}{R_{1} +R_{2}}N_{1}I_{1}-\frac {R_{1}}{R_{1} +R_{2}}N_{2}I_{2}&=& \frac {R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_{1} +R_{2}}\mathit {\Phi}_{3} \\[ 5pt ] R_{2}N_{1}I_{1}-R_{1}N_{2}I_{2}&=& (R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1})\mathit {\Phi}_{3} \\[ 5pt ] \mathit {\Phi}_{3}&=&\frac {R_{2}N_{1}I_{1}-R_{1}N_{2}I_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
(4)の解答式に各値を代入すると，
\[
\begin{eqnarray}
\mathit {\Phi}_{3}&=&\frac {R_{2}N_{1}I_{1}-R_{1}N_{2}I_{2}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}} \\[ 5pt ] 0.5\times 10^{-3}&=&\frac {1.0\times 10^{7}\times 500\times 0.9-2.0\times 10^{5}\times 2\times I_{2}}{2.0\times 10^{5}\times 1.0\times 10^{7}+1.0\times 10^{7}\times 2.0\times 10^{5}+2.0\times 10^{5}\times 2.0\times 10^{5}} \\[ 5pt ] 0.5\times 10^{-3}&=&\frac {45000-4 I_{2}}{4.04\times 10^{7}} \\[ 5pt ] 45000-4 I_{2}&=&20200 \\[ 5pt ] I_{2}&=&6200 \ \mathrm {[A]}　→　6.2 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。