《理論》〈電気回路〉[H27:問3] テブナンの定理に関する計算問題

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

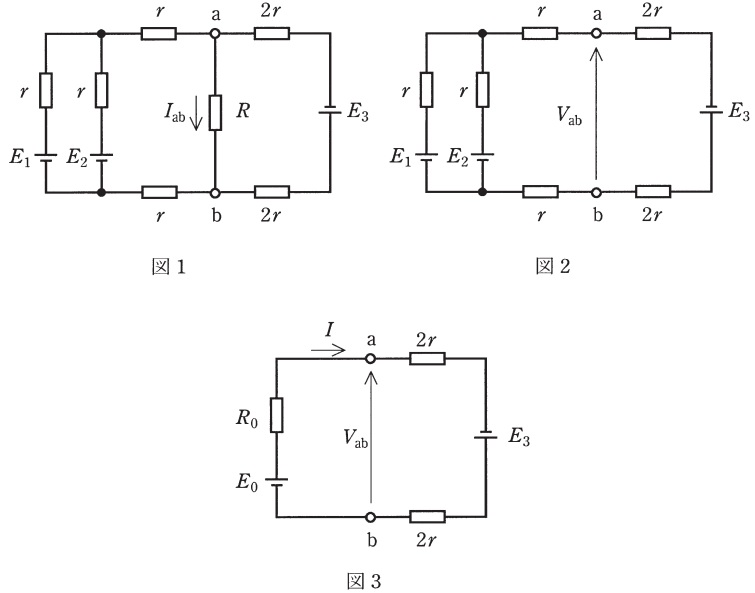
図1に示す回路において，抵抗$ \ R \ $に流れる$ \ I_{\mathrm {ab}} \ $をテブナンの定理を用いて求めたい。

まず，抵抗$ \ R \ $を取り除いた図2の回路は，端子$ \ \mathrm {a-b} \ $間から左側部分を整理すると図3のように表される。図3の電圧$ \ E_{0} \ $は$ \ E_{0}= \ \fbox {　（１）　} \ $，抵抗$ \ R_{0} \ $は$ \ \displaystyle R_{0}=\frac {5}{2}r \ $となる。

図3に示すように電流$ \ I \ $をとれば$ \ I= \ \fbox {　（２）　} \ $となるから，端子$ \ \mathrm {a-b} \ $間に現れる電圧$ \ V_{\mathrm {ab}} \ $(端子$ \ \mathrm {b} \ $を基準とする)は$ \ V_{\mathrm {ab}}= \ \fbox {　（３）　} \ $となる。

次に，図3の直流電圧源を短絡除去した場合において，端子$ \ \mathrm {a-b} \ $間から回路をみた抵抗$ \ R_{\mathrm {ab}} \ $は，$ \ R_{\mathrm {ab}}= \ \fbox {　（４）　} \ $となるから，$ \ \fbox {　（３）　} \ $及び$ \ \fbox {　（４）　} \ $より，$ \ R \ $に流れる電流$ \ I_{\mathrm {ab}} \ $は，$ \ I_{\mathrm {ab}}= \ \fbox {　（５）　} \ $となる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {E_{1}-E_{2}}{2}　　　　　&（ロ）&　\frac {2(E_{1}+E_{2})-E_{3}}{13R+21r}　　　　　&（ハ）&　2r \\[ 5pt ] &（ニ）&　\frac {2(E_{1}+E_{2})-E_{3}}{13}　　　　　&（ホ）&　\frac {4(E_{1}+E_{2})-5E_{3}}{13R+20r}　　　　　&（ヘ）&　E_{1}+E_{2} \\[ 5pt ] &（ト）&　\frac {21}{13}r　　　　　&（チ）&　\frac {E_{1}+E_{2}+2E_{3}}{13r}　　　　　&（リ）&　\frac {E_{1}+E_{2}-2E_{3}}{4} \\[ 5pt ] &（ヌ）&　\frac {E_{1}+E_{2}+2E_{3}}{16r}　　　　　&（ル）&　\frac {E_{1}+E_{2}}{2}　　　　　&（ヲ）&　\frac {20}{13}r \\[ 5pt ] &（ワ）&　\frac {E_{1}+E_{2}-2E_{3}}{4R+8r}　　　　　&（カ）&　\frac {2(E_{1}+E_{2}+E_{3})}{13r}　　　　　&（ヨ）&　\frac {4(E_{1}+E_{2})-5E_{3}}{13}
\end{eqnarray}
\]

【ワンポイント解説】

(1)の電圧源を電流源に置き換え，さらに整理する計算が解けるかどうかで点数差がついてしまう非常に怖い問題です。電気回路の問題は最初を間違えると全部間違えてしまう可能性があるので，慎重に計算するようにしましょう。

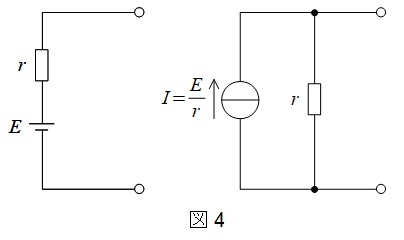
1.電圧源と電流源の等価変換
図4に示すように，電圧源と電流源は直列と並列で等価変換することができます。

2.テブナンの定理
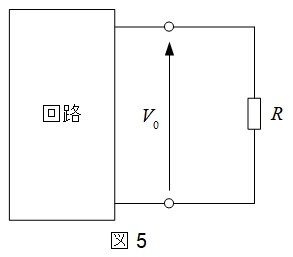
　図5において回路中の2端子の開放電圧を$ \ V_{0} \ $，電圧源を短絡し，電流源を開放した時の端子から見た合成抵抗を$ \ R_{0} \ $とした時，外部抵抗$ \ R \ $とした時，抵抗$ \ R \ $を流れる電流$ \ I \ $は，下式の通りとなります。
\[
I=\frac {V_{0}}{R+R_{0}}
\]

【関連する「電気の神髄」記事】

　　鳳・テブナンの定理の証明
　　重ね合わせの理の証明

【解答】

(1)解答：ル
図1の端子$ \ \mathrm {a-b} \ $の左側を電流源の等価変換をすると，図6の通りとなる。

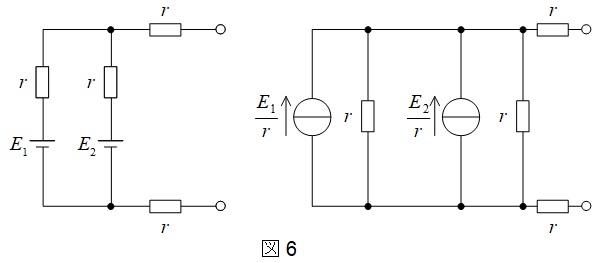
これより，電流源と並列抵抗を合成すると，図7のようになり，電流源を電圧源に等価変換することができる。

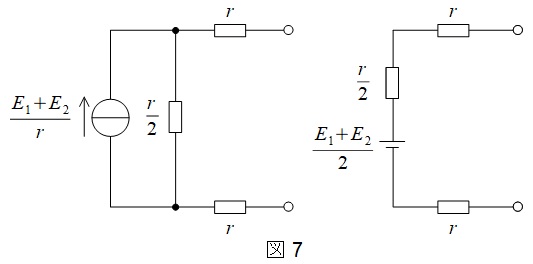
よって，
\[
E_{0}=\frac {E_{1}+E_{2}}{2}
\] となる。

(2)解答：チ
図3の回路方程式より電流$ \ I \ $を求めると，
\[
\begin{eqnarray}
E_{0}+E_{3}&=&R_{0}I+2rI+2rI \\[ 5pt ] \frac {E_{1}+E_{2}}{2}+E_{3}&=&\frac {5}{2}rI+2rI+2rI \\[ 5pt ] \frac {E_{1}+E_{2}+2E_{3}}{2}&=&\frac {13}{2}rI \\[ 5pt ] E_{1}+E_{2}+2E_{3}&=&13rI \\[ 5pt ] I&=&\frac {E_{1}+E_{2}+2E_{3}}{13r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヨ
図3より，
\[
\begin{eqnarray}
V_{\mathrm {ab}}&=&E_{0}-R_{0}I \\[ 5pt ] &=&\frac {E_{1}+E_{2}}{2}-\frac {5}{2}r\cdot \frac {E_{1}+E_{2}+2E_{3}}{13r} \\[ 5pt ] &=&\frac {8(E_{1}+E_{2})-10E_{3}}{26} \\[ 5pt ] &=&\frac {4(E_{1}+E_{2})-5E_{3}}{13} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヲ
図3において，合成抵抗$ \ R_{\mathrm {ab}} \ $は，
\[
\begin{eqnarray}
R_{\mathrm {ab}}&=&\frac {R_{0}\cdot 4r}{R_{0}+4r} \\[ 5pt ] &=&\frac {\displaystyle \frac {5}{2}r\cdot 4r}{\displaystyle \frac {5}{2}r+4r} \\[ 5pt ] &=&\frac {20r}{13} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
ワンポイント解説「2.テブナンの定理」より，$ \ R \ $に流れる電流$ \ I_{\mathrm {ab}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {ab}}&=&\frac {V_{\mathrm {ab}}}{R+R_{\mathrm {ab}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {4(E_{1}+E_{2})-5E_{3}}{13}}{\displaystyle R+\frac {20r}{13}} \\[ 5pt ] &=&\frac {4(E_{1}+E_{2})-5E_{3}}{13R+20r} \\[ 5pt ] \end{eqnarray}
\] と求められる。