《理論》〈電磁気〉[R01:問1] リング状電荷が作る電界に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，真空中のリング状電荷が作る電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

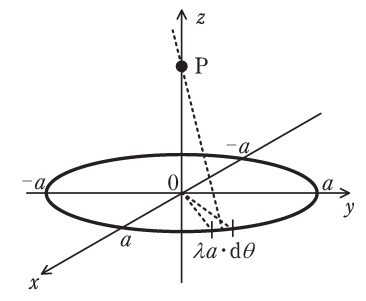
図のように，\( \ xy \ \)平面上に原点を中心とした半径\( \ a \ \)のリング状電荷があり，その線電荷密度は\( \ \lambda \ \)である。なお，真空中の誘電率を\( \ \varepsilon _{0} \ \)とする。

リング状電荷の微小角\( \ \mathrm {d}\theta \ \)の円弧の電荷\( \ \lambda a \cdot \mathrm {d}\theta \ \)により点\( \ \mathrm {P}\left( 0，0，z\right) \ \)に生じる電界の大きさは\( \ \fbox {　 （１） 　} \ \)である。この電界の\( \ z \ \)方向成分を\( \ \theta \ \)について積分することで，リング状電荷全体が点\( \ \mathrm {P} \ \)に作る電界の\( \ z \ \)方向成分は\( \ \fbox {　 （２） 　} \ \)と求められる。\( \ z≧0 \ \)において，その大きさが最も大きい点\( \ \mathrm {P} \ \)の\( \ z \ \)座標は\( \ \fbox {　 （３） 　} \ \)である。また，原点の電界は\( \ \fbox {　 （４） 　} \ \)で，無限遠を基準とした原点の電位は\( \ \fbox {　 （５） 　} \ \)である。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\lambda \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}\sqrt {z^{2}+a^{2}}}　　　　　&（ロ）&　\frac {\lambda z^{2} }{2 \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}　　　　　&（ハ）&　\frac {\lambda a }{2\varepsilon _{0}\sqrt {z^{2}+a^{2}}} \\[ 5pt ] &（ニ）&　\frac {\lambda z \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) }　　　　　&（ホ）&　\frac {\lambda }{2 \varepsilon _{0}}　　　　　&（ヘ）&　\frac {\lambda }{2 \varepsilon _{0}a} \\[ 5pt ] &（ト）&　\frac {1}{2}a　　　　　&（チ）&　\frac {\lambda az }{2 \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}　　　　　&（リ）&　\frac {\sqrt {2}}{2}a \\[ 5pt ] &（ヌ）&　\frac {\lambda }{4 \varepsilon _{0}}　　　　　&（ル）&　a　　　　　&（ヲ）&　0 \\[ 5pt ] &（ワ）&　\frac {\lambda a \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) }　　　　　&（カ）&　\frac {\sqrt {2}\lambda }{2 \varepsilon _{0}}　　　&（ヨ）&　\frac {\lambda }{4 \varepsilon _{0}a} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

円電流が作る電界に関する問題です。近年1種ではかなり高い確率で円電流を使用した問題が出題されているため，本年も予想通り出題されたという印象です。途中の微分積分計算にやや時間がかかるかもしれません。特に(5)は計算の工夫が必要で，1種らしい問題と言えます。

1.点電荷が作る電界の強さ\( \ E \ \)
真空中で\( \ Q \ \)が作る電界の大きさ\( \ E \ \)は，距離\( \ r \ \)の地点で，
\[
\begin{eqnarray}
E&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.割り算の微分の公式
\( \ \displaystyle y=\frac {u(x)}{v(x)} \ \)で示される関数の微分は，
\[
\begin{eqnarray}
\frac {dy}{dx}&=&\frac {u^{\prime }v-uv^{\prime }}{v^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.電位\( \ V \ \)と電界\( \ E \ \)の関係
電界の大きさ\( \ E(r) \ \)で表せるとき，中心から\( \ a \ \)の地点と\( \ b \ \)の地点の電位差は，
\[
\begin{eqnarray}
V=-\int ^{b}_{a}E(r)\mathrm {d}r \\[ 5pt ] \end{eqnarray}　
\] となります。

【解答】

(1)解答：ワ
リング状電荷の微小角\( \ \mathrm {d}\theta \ \)から点\( \ \mathrm {P} \ \)までの距離\( \ r \ \)は，
\[
\begin{eqnarray}
r&=&\sqrt {a^{2}+z^{2}} \\[ 5pt ] \end{eqnarray}
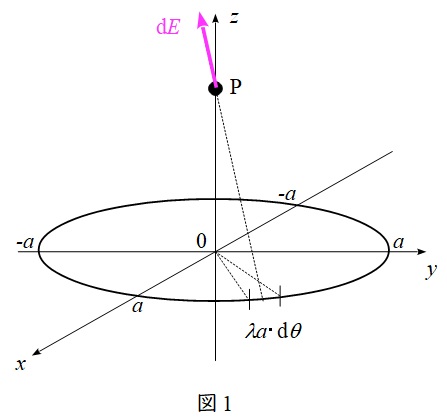
\] であるから，ワンポイント解説「1.点電荷が作る電界の強さ\( \ E \ \)」より，リング状電荷の微小角\( \ \mathrm {d}\theta \ \)の円弧の電荷\( \ \lambda a \cdot \mathrm {d}\theta \ \)により点\( \ \mathrm {P} \ \)に生じる電界の大きさ\( \ \mathrm {d}E \ \)は，
\[
\begin{eqnarray}
\mathrm {d}E&=&\frac {\lambda a \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] &=&\frac {\lambda a \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
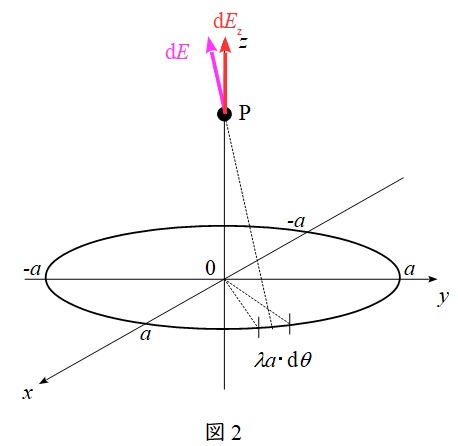
(1)及び図2より，リング状電荷の微小角\( \ \mathrm {d}\theta \ \)の電荷により，点\( \ \mathrm {P} \ \)に生じる\( \ z \ \)成分の電界の大きさ\( \ \mathrm {d}E_{\mathrm {z}} \ \)は，
\[
\begin{eqnarray}
\mathrm {d}E_{\mathrm {z}}&=&\frac {z }{\sqrt {a^{2}+z^{2}}}\mathrm {d}E \\[ 5pt ] &=&\frac {z }{\sqrt {a^{2}+z^{2}}}\times \frac {\lambda a \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) } \\[ 5pt ] &=& \frac {\lambda az \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] となる。リング状電荷全体が点\( \ \mathrm {P} \ \)に作る電界の\( \ z \ \)方向成分は，これを周回積分したものであるから，
\[
\begin{eqnarray}
E_{\mathrm {z}}&=&\int \mathrm {d}E_{\mathrm {z}} \\[ 5pt ] &=&\int ^{2\pi }_{0}\frac {\lambda az \cdot \mathrm {d}\theta }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] &=&\frac {\lambda az }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}\int ^{2\pi }_{0} 1 \mathrm {d}\theta \\[ 5pt ] &=&\frac {\lambda az }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}\left[ \theta \right] ^{2\pi }_{0} \\[ 5pt ] &=&\frac {\lambda az }{4\pi \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}\times 2\pi \\[ 5pt ] &=&\frac {\lambda az }{2 \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
ワンポイント解説「2.割り算の微分の公式」の通り，(2)の解答式の両辺を\( \ z \ \)について微分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}E_{\mathrm {z}}}{\mathrm {d}z}&=&\frac {\mathrm {d}}{\mathrm {d}z}\left\{ \frac {\lambda az }{2 \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}\right\} \\[ 5pt ] &=&\frac {\lambda a }{2 \varepsilon _{0}}\frac {\mathrm {d}}{\mathrm {d}z}\left\{ \frac {z }{\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}\right\} \\[ 5pt ] &=&\frac {\lambda a }{2 \varepsilon _{0}} \cdot \frac {\displaystyle \left( z^{2}+a^{2}\right) ^{\frac {3}{2}}-z\cdot \frac {3}{2} \cdot 2z \left( z^{2}+a^{2}\right) ^{\frac {1}{2}}}{\left( z^{2}+a^{2}\right) ^{3}} \\[ 5pt ] &=&\frac {\lambda a }{2 \varepsilon _{0}}\cdot \frac {\displaystyle \left( z^{2}+a^{2}\right) ^{\frac {3}{2}}-3z^{2} \left( z^{2}+a^{2}\right) ^{\frac {1}{2}}}{\left( z^{2}+a^{2}\right) ^{3}} \\[ 5pt ] &=&\frac {\lambda a }{2 \varepsilon _{0}} \cdot \frac {\displaystyle \left( z^{2}+a^{2}\right) -3z^{2} }{\left( z^{2}+a^{2}\right) ^{\frac {5}{2}}} \\[ 5pt ] &=&\frac {\lambda a }{2 \varepsilon _{0}} \cdot \frac {\displaystyle a^{2}-2z^{2} }{\left( z^{2}+a^{2}\right) ^{\frac {5}{2}}} \\[ 5pt ] \end{eqnarray}
\] となる。電界が最大となるのは，\( \ \displaystyle \frac {\mathrm {d}E_{\mathrm {z}}}{\mathrm {d}z}=0 \ \)の時であるから，その時の\( \ z \ \)は，
\[
\begin{eqnarray}
a^{2}-2z^{2}&=&0 \\[ 5pt ] 2z^{2}&=&a^{2} \\[ 5pt ] z^{2}&=&\frac {a^{2}}{2} \\[ 5pt ] z&=&\frac {a}{\sqrt {2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヲ
(2)の解答式に\( \ z=0 \ \)を代入すると，\( \ E_{\mathrm {z}}=0 \ \)と求められる。

(5)解答：ホ
ワンポイント解説「3.電位\( \ V \ \)と電界\( \ E \ \)の関係」より，無限遠を基準とした原点の電位は，
\[
\begin{eqnarray}
V&=&-\int ^{0}_{\infty }E_{\mathrm {z}}\mathrm {d}z \\[ 5pt ] &=&-\int ^{0}_{\infty }\frac {\lambda az }{2 \varepsilon _{0}\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}\mathrm {d}z \\[ 5pt ] &=&-\frac {\lambda a }{2 \varepsilon _{0}}\int ^{0}_{\infty }\frac {z }{\left( z^{2}+a^{2}\right) ^{\frac {3}{2}}}\mathrm {d}z \\[ 5pt ] &=&-\frac {\lambda a }{2 \varepsilon _{0}}\left[ -\frac {1}{\left( z^{2}+a^{2}\right) ^{\frac {1}{2}}} \right] ^{0}_{\infty } \\[ 5pt ] &=&-\frac {\lambda a }{2 \varepsilon _{0}}\left( -\frac {1}{a} \right) \\[ 5pt ] &=&\frac {\lambda }{2 \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}　
\] と求められる。