【問題】
【難易度】★★★☆☆(普通)
次の文章は,回路の過渡現象に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。
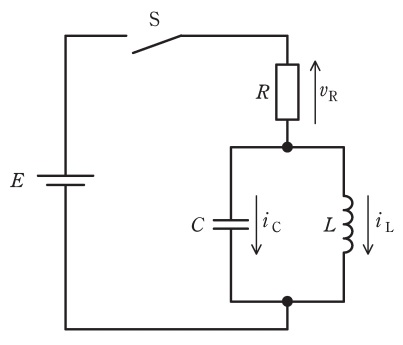
図の回路は,時刻\( \ t<0 \ \)ではスイッチ\( \ \mathrm {S} \ \)は開いており,キャパシタ\( \ C \ \)の電荷\( \ q \ \)は\( \ 0 \ \)である。
時刻\( \ t=0 \ \)でスイッチ\( \ \mathrm {S} \ \)を閉じると,時刻\( \ t≧0 \ \)では電圧に関する以下の二つの微分方程式
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+\fbox { (1) } &=& E &・・・・・・・・・・ ①& \\[ 5pt ]
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}-\fbox { (2) } &=& 0 &・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
が成立する,
上記の①式及び②式から,インダクタ\( \ L \ \)の電流\( \ i_{\mathrm {L}} \ \)に関する微分方程式
\[
\begin{eqnarray}
\fbox { (3) }+L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+Ri_{\mathrm {L}} &=& E \\[ 5pt ]
\end{eqnarray}
\]
を得る。
したがって,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm {R}} \ \)が振動的となる条件は,
\[
\begin{eqnarray}
\fbox { (4) } &<& 0 \\[ 5pt ]
\end{eqnarray}
\]
で与えられる。
また,スイッチ\( \ \mathrm {S} \ \)を閉じて十分時間が経過し,回路が定常状態になった時のキャパシタ\( \ C \ \)の電荷は,
\[
\begin{eqnarray}
q &=& \fbox { (5) } \\[ 5pt ]
\end{eqnarray}
\]
となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {1}{2}CE^{2} &(ロ)& CE &(ハ)& R\left( i_{\mathrm {L}}+i_{\mathrm {C}}\right) \\[ 5pt ]
&(ニ)& L-4R^{2}C &(ホ)& Ri_{\mathrm {L}} &(ヘ)& Ri_{\mathrm {C}} \\[ 5pt ]
&(ト)& \frac {1}{RC}\int i_{\mathrm {C}}\mathrm {d}t &(チ)& 0 &(リ)& RLC\frac {\mathrm {d}^{2}i_{\mathrm {L}}}{\mathrm {d}t^{2}} \\[ 5pt ]
&(ヌ)& \int i_{\mathrm {C}}\mathrm {d}t &(ル)& 4R^{2}C-L &(ヲ)& LC\frac {\mathrm {d}^{2}i_{\mathrm {L}}}{\mathrm {d}t^{2}} \\[ 5pt ]
&(ワ)& 4R^{2}C+L &(カ)& \frac {1}{C}\int i_{\mathrm {C}}\mathrm {d}t &(ヨ)& RC\frac {\mathrm {d}^{2}i_{\mathrm {L}}}{\mathrm {d}t^{2}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
過渡現象に関する問題は非常によく出題されやすいです。本問の場合は(2)から(3)を導き出すところに若干工夫が必要となります。計算方法をよく理解するようにしましょう。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ V_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ V_{\mathrm{L}} \ \),コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \ln {x} &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=Ae^{-\alpha t} \left( A=e^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)解答:ハ
抵抗\( \ R \ \)の電流\( \ i_{\mathrm {R}} \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {R}} &=& i_{\mathrm {L}}+i_{\mathrm {C}} \\[ 5pt ]
\end{eqnarray}
\]
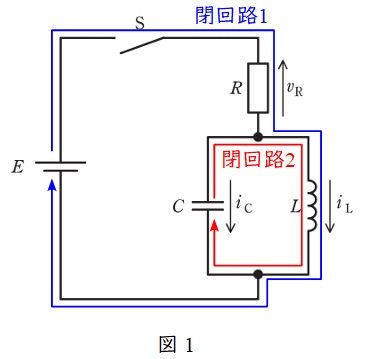
であるから,図1の閉回路1に関する回路方程式は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+Ri_{\mathrm {R}} &=& E\\[ 5pt ]
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+R\left( i_{\mathrm {L}}+i_{\mathrm {C}}\right) &=& E\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:カ
(1)と同様に,図1の閉回路2に関する回路方程式は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}-\frac {1}{C}\int i_{\mathrm {C}}\mathrm {d}t &=& 0\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
②を時間\( \ t \ \)で微分すると,
\[
\begin{eqnarray}
L\frac {\mathrm {d}^{2}i_{\mathrm {L}}}{\mathrm {d}t^{2}}-\frac {i_{\mathrm {C}}}{C} &=& 0 \\[ 5pt ]
i_{\mathrm {C}} &=& LC\frac {\mathrm {d}^{2}i_{\mathrm {L}}}{\mathrm {d}t^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを①に代入すると,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+R\left( i_{\mathrm {L}}+i_{\mathrm {C}}\right) &=& E \\[ 5pt ]
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+R\left( i_{\mathrm {L}}+LC\frac {\mathrm {d}^{2}i_{\mathrm {L}}}{\mathrm {d}t^{2}}\right) &=& E \\[ 5pt ]
RLC\frac {\mathrm {d}^{2}i_{\mathrm {L}}}{\mathrm {d}t^{2}}+L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+Ri_{\mathrm {L}} &=& E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ニ
(3)の解答式の定常解を\( \ i_{\mathrm {Ls}} \ \),過渡解を\( \ i_{\mathrm {Lt}} \ \)とすると,\( \ \displaystyle \frac {\mathrm {d}^{2}i_{\mathrm {Ls}}}{\mathrm {d}t^{2}}=\displaystyle \frac {\mathrm {d}i_{\mathrm {Ls}}}{\mathrm {d}t}=0 \ \)であるから,
\[
\begin{eqnarray}
Ri_{\mathrm {Ls}} &=& E \\[ 5pt ]
i_{\mathrm {Ls}} &=& \frac {E}{R} \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,過渡解は\( \ E=0 \ \)とすると,
\[
\begin{eqnarray}
RLC\frac {\mathrm {d}^{2}i_{\mathrm {Lt}}}{\mathrm {d}t^{2}}+L\frac {\mathrm {d}i_{\mathrm {Lt}}}{\mathrm {d}t}+Ri_{\mathrm {Lt}} &=& 0 &・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ i_{\mathrm {Lt}}=Ae^{\beta t} \ \)と置くと,
\[
\begin{eqnarray}
\frac {\mathrm {d}i_{\mathrm {Lt}}}{\mathrm {d}t} &=& \beta Ae^{\beta t} \\[ 5pt ]
\frac {\mathrm {d}^{2}i_{\mathrm {Lt}}}{\mathrm {d}t^{2}} &=& \beta ^{2}Ae^{\beta t} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,これを③に代入すると,
\[
\begin{eqnarray}
RLC\beta ^{2}Ae^{\beta t}+L\beta Ae^{\beta t}+RAe^{\beta t} &=& 0 \\[ 5pt ]
RLC\beta ^{2}+L\beta+R&=& 0 \\[ 5pt ]
\beta &=&\frac {-L±\sqrt {L^{2}-4R^{2}LC}}{2RLC}
\end{eqnarray}
\]
となる。ここで,振動的となるためには上式の根号部が負と値とならなければならないので,
\[
\begin{eqnarray}
L^{2}-4R^{2}LC &<& 0 \\[ 5pt ]
L-4R^{2}C &<& 0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:チ
十分時間が経過すると,インダクタに流れる電流\( \ \displaystyle i_{\mathrm {L}}=i_{\mathrm {Ls}}= \frac {E}{R} \ \)となり,インダクタでの電圧降下\( \ \displaystyle L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}=0 \ \)となる。よって,②より,
\[
\begin{eqnarray}
\frac {1}{C}\int i_{\mathrm {C}}\mathrm {d}t &=& 0 \\[ 5pt ]
\frac {q}{C} &=& 0 \\[ 5pt ]
q &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん