《理論》〈電磁気〉[H29:問1] コイルに蓄えられるエネルギーに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，コイルに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

空気中の広い空間にインダクタンス$ \ L_{0} \ $のコイルがあり，理想的な電流源に接続され，常に一定の電流$ \ I \ $が流れている。コイルの巻線抵抗は無視できるものとする。このとき，コイルに蓄えられているエネルギーは$ \ \fbox {　（１）　} \ $である。
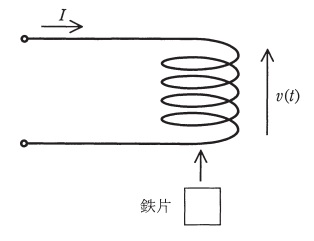
次に，十分遠方にある鉄片を，図のように時刻$ \ t=0 \ $からコイルにゆっくりと近付けることでコイルのインダクタンス$ \ L(t) \ $を時間変化させ，$ \ t=T \ $で鉄片の動きを止めた。ただし，鉄片の磁束の飽和やヒステリシス特性は無視できるものとする。$ \ t=0～T \ $の間，図に示された向きでコイルの電圧$ \ v(t) \ $と測定すれば，電磁誘導の法則から$ \ v(t)=\fbox {　（２）　} \ $が成り立つので，インダクタンス$ \ L(t) \ $は$ \ v(t) \ $を用いて$ \ L(t)=\fbox {　（３）　} \ $の式で計算できることが分かる。
$ \ L(T)=L_{1} \ $とすると，$ \ t=0～T \ $の間に電流源から供給されるエネルギーは$ \ \fbox {　（４）　} \ $であり，鉄片の動きによりコイルが外部にした仕事量は$ \ \fbox {　（５）　} \ $である。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {1}{2}(L_{1}-L_{0})I^{2}　　　&（ロ）&　\frac {v(t)T}{I}　　　&（ハ）&　\frac {2}{3}(L_{1}-L_{0})I^{2} \\[ 5pt ] &（ニ）&　L_{0}+\frac {1}{I}\int ^{t}_{0}v(\tau )\mathrm {d}\tau　　　&（ホ）&　\frac {L(t)I}{T}　　　&（ヘ）&　\frac {3}{2}(L_{1}-L_{0})I^{2} \\[ 5pt ] &（ト）&　\frac {1}{2}L_{0}I^{2}　　　&（チ）&　\frac {1}{I}\int ^{t}_{0}v(\tau )\mathrm {d}\tau　　　&（リ）&　0 \\[ 5pt ] &（ヌ）&　2(L_{1}-L_{0})I^{2}　　　&（ル）&　2L_{0}I^{2}　　　&（ヲ）&　L_{0}I^{2} \\[ 5pt ] &（ワ）&　\frac {\mathrm {d}}{\mathrm {d}t}[L(t)I]　　　&（カ）&　(L_{1}-L_{0})I^{2}　　　&（ヨ）&　\frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}}[L(t)TI] \end{eqnarray}
\]

【ワンポイント解説】

コイルに蓄えられるエネルギーに関する問題で，近年あまり見たことがない問題です。ただし，内容自体はそれほど難易度が高いものではないので，落ち着いて解いていきましょう。

1.コイルに蓄えられるエネルギー$ \ W \ $
インダクタンス$L$に電流$I$を流すことにより蓄えられるエネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W&=&\frac {1}{2}LI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

2.コイルに発生する電圧$ \ v(t) \ $
インダクタンス$ \ L(t) \ $に一定電流$ \ I \ $を流すことにより発生する電圧$ \ v(t) \ $は，
\[
\begin{eqnarray}
v(t)&=&\frac {\mathrm {d}L(t)}{\mathrm {d}t}I \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ト
最初にコイルに蓄えられているエネルギー$ \ W_{0} \ $は，
\[
\begin{eqnarray}
W_{0}&=&\frac {1}{2}L_{0}I^{2} \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ワ
$t=0～T$の間，コイルに発生する電圧は，
\[
\begin{eqnarray}
v(t)&=&\frac {\mathrm {d}L(t)}{\mathrm {d}t}I=\frac {\mathrm {d}}{\mathrm {d}t}[L(t)I] \\[ 5pt ] \end{eqnarray}
\] となる。

(3)解答：ニ
(2)より，$ \ \displaystyle v(t)=\frac {\mathrm {d}L(t)}{\mathrm {d}t}I \ $であるから，式を変形すると，
\[
\begin{eqnarray}
\mathrm {d}L(t)&=&\frac {1}{I}v(t)\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，両辺を積分すると，
\[
\begin{eqnarray}
L(t)&=&\frac {1}{I}\int ^{t}_{0}v(\tau )\mathrm {d}\tau +C　(Cは積分定数) \\[ 5pt ] \end{eqnarray}
\] となる。ここで，題意より$ \ L(0)=L_{0} \ $であるから，$ \ C=L_{0} \ $となるため，
\[
\begin{eqnarray}
L(t)&=&L_{0}+\frac {1}{I}\int ^{t}_{0}v(\tau )\mathrm {d}\tau \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：カ
$t=0～T$の間に電流源から供給されるエネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W&=&\int ^{T}_{0} v(t)I\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，(1)より$ \ \displaystyle v(t)=\frac {\mathrm {d}L(t)}{\mathrm {d}t}I \ $であり，インダクタンスは$ \ t=0 \ $の時$ \ L_{0} \ $，$ \ t=T \ $の時$ \ L_{1} \ $であるから，
\[
\begin{eqnarray}
W &=& \int ^{T}_{0} v(t)I\mathrm {d}t \\[ 5pt ] &=& \int ^{L_{1}}_{L_{0}} \frac {\mathrm {d}L(t)}{\mathrm {d}t}I\cdot I\mathrm {d}t \\[ 5pt ] &=& \int ^{L_{1}}_{L_{0}} I^{2}\mathrm {d}L(t) \\[ 5pt ] \end{eqnarray}
\] となり，これを計算すると，
\[
\begin{eqnarray}
W &=& \left[ L(t)\right] ^{L_{1}}_{L_{0}} I^{2} \\[ 5pt ] &=& (L_{1}-L_{0}) I^{2} \\[ 5pt ] \end{eqnarray}
\] となる。

(5)解答：イ
インダクタンスが$ \ t=0 \ $の時$ \ L_{0} \ $，$ \ t=T \ $の時$ \ L_{1} \ $であるから，鉄片の動きによりコイルが外部にした仕事量$ \ W_{\mathrm {o}} \ $は，
\[
\begin{eqnarray}
W_{\mathrm {o}} &=& \frac {1}{2}L_{1}I^{2}-\frac {1}{2}L_{0}I^{2} \\[ 5pt ] &=& \frac {1}{2}(L_{1}-L_{0})I^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。