【問題】
【難易度】★★★☆☆(普通)
次の文章は,アンペア(アンペール)の周回積分の法則に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
一般に,空間上の磁界ベクトルを\( \ \boldsymbol H \ \),\( \ \mathrm {C} \ \)を閉曲線,\( \ \mathrm {d}\boldsymbol l \ \)を\( \ \mathrm {C} \ \)上の微小区間ベクトル,\( \ I \ \)を\( \ \mathrm {C} \ \)と鎖交する電流の総量とすると,アンペアの周回積分の法則は①式のようになる。
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I ・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
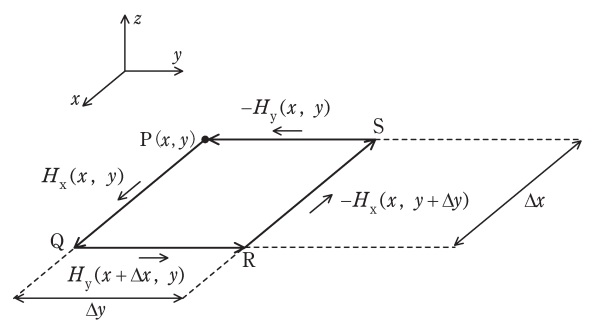
ここで,直交座標空間上において,\( \ z \ \)軸の正方向に一様な電流が流れている時の磁界\( \ \boldsymbol H \ \)を考える。電流の面密度は\( \ J_{\mathrm {z}} \ \)である。図のように,\( \ z \ \)軸と垂直で微小な長方形の積分路を仮定する。積分路は点\( \ \mathrm {P}\left( x,y \right) \ \)から点\( \ \mathrm {Q} \ \),\( \ \mathrm {R} \ \),\( \ \mathrm {S} \ \)を経て点\( \ \mathrm {P} \ \)に戻る閉路であり,辺\( \ \mathrm {PQ} \ \)及び辺\( \ \mathrm {RS} \ \)の長さは\( \ \Delta x \ \),辺\( \ \mathrm {QR} \ \)及び\( \ \mathrm {SP} \ \)の長さは\( \ \Delta y \ \)である。また,\( \ z \ \)軸方向の磁界は\( \ 0 \ \)であるので,\( \ \boldsymbol H=\left( H_{\mathrm {x}}\left( x,y \right) ,H_{\mathrm {y}}\left( x,y \right) ,0 \right) \ \)とし,\( \ x- y \ \)平面上で考える。
このとき,積分路\( \ \mathrm {PQRS} \ \)を閉曲線\( \ \mathrm {C} \ \)として①式を適用する。まず辺\( \ \mathrm {PQ} \ \)を考え,\( \ \mathrm {PQ} \ \)に平行な\( \ \mathrm {PQ} \ \)上の磁界を\( \ H_{\mathrm {x}}\left( x,y \right) \ \)と近似すると,\( \ \mathrm {PQ} \ \)に沿った\( \ \boldsymbol H \ \)の線積分は\( \ \fbox { (1) } \ \)である。同様に,辺\( \ \mathrm {QR} \ \),\( \ \mathrm {RS} \ \),\( \ \mathrm {SP} \ \)に平行な磁界をそれぞれ\( \ H_{\mathrm {y}}\left( x+\Delta x,y \right) \ \),\( \ -H_{\mathrm {x}}\left( x,y+\Delta y \right) \ \),\( \ -H_{\mathrm {y}}\left( x,y \right) \ \)と近似すると,①式の左辺は\( \ \fbox { (2) } \ \)である。一方,①式の右辺は,この積分路に鎖交する電流\( \ I \ \)なので\( \ \fbox { (3) } \ \)である。したがって,①式より\( \ \fbox { (4) } \ \)が導かれる。
\( \ \Delta x \ \),\( \ \Delta y \ \)をともに\( \ 0 \ \)に近づけると,電流密度ベクトルを\( \ \boldsymbol J \ \)としたときに\( \ \fbox { (5) } \ \)のように表されるアンペアの法則の微分形における\( \ z \ \)方向成分と同じ式になる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {H_{\mathrm {y}}\left( x+\Delta x,y \right) -H_{\mathrm {y}}\left( x,y \right) }{\Delta y}-\frac {H_{\mathrm {x}}\left( x,y+\Delta y \right) -H_{\mathrm {x}}\left( x,y \right) }{\Delta x}=J_{\mathrm {z}} \\[ 5pt ]
&(ロ)& \frac {H_{\mathrm {x}}\left( x,y \right) }{\Delta x}+\frac {H_{\mathrm {y}}\left( x+\Delta x,y \right) }{\Delta y}-\frac {H_{\mathrm {x}}\left( x,y+\Delta y \right) }{\Delta x}-\frac {H_{\mathrm {y}}\left( x,y \right) }{\Delta y} \\[ 5pt ]
&(ハ)& H_{\mathrm {x}}\left( x,y \right) \cdot \Delta y +H_{\mathrm {y}}\left( x+\Delta x,y \right) \cdot \Delta x -H_{\mathrm {x}}\left( x,y+\Delta y \right) \cdot \Delta y-H_{\mathrm {y}}\left( x,y \right) \cdot \Delta x \\[ 5pt ]
&(ニ)& H_{\mathrm {x}}\left( x,y \right) \cdot \Delta x +H_{\mathrm {y}}\left( x+\Delta x,y \right) \cdot \Delta y -H_{\mathrm {x}}\left( x,y+\Delta y \right) \cdot \Delta x-H_{\mathrm {y}}\left( x,y \right) \cdot \Delta y \\[ 5pt ]
&(ホ)& \frac {H_{\mathrm {y}}\left( x+\Delta x,y \right) -H_{\mathrm {y}}\left( x,y \right) }{\Delta x}-\frac {H_{\mathrm {x}}\left( x,y+\Delta y \right) -H_{\mathrm {x}}\left( x,y \right) }{\Delta y}=J_{\mathrm {z}} \\[ 5pt ]
&(ヘ)& \frac {H_{\mathrm {y}}\left( x+\Delta x,y \right) -H_{\mathrm {y}}\left( x,y \right) }{\Delta x\cdot \Delta y }-\frac {H_{\mathrm {x}}\left( x,y+\Delta y \right) -H_{\mathrm {x}}\left( x,y \right) }{\Delta x\cdot \Delta y }=J_{\mathrm {z}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ト)& H_{\mathrm {x}}\left( x,y \right) \cdot \Delta x &(チ)& \mathrm {div} \boldsymbol H =0 &(リ)& J_{\mathrm {z}}\cdot \Delta x \cdot \Delta y \\[ 5pt ]
&(ヌ)& J_{\mathrm {z}} &(ル)& \frac {H_{\mathrm {x}}\left( x,y \right) }{\Delta x} &(ヲ)& \mathrm {rot} \boldsymbol H =\boldsymbol J \\[ 5pt ]
&(ワ)& \mathrm {rot} \boldsymbol J =\boldsymbol H &(カ)& \frac {J_{\mathrm {z}}}{\Delta x \cdot \Delta y } &(ヨ)& H_{\mathrm {x}}\left( x,y \right) \cdot \Delta y \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
本格的な電磁気の教科書の内容であり,やや難しそうに見えますが,問題としては文章をよく読み考えると解ける問題となっています。
回転\( \ \mathrm {rot} \ \)の内容等は専門書を読み進めると出てくる内容なので,\( \ 1 \ \)種受験生ならば覚えておいた方が良いと思います。
1.アンペア(アンペール)の周回積分の法則
空間上の磁界ベクトルを\( \ \boldsymbol H \ \),\( \ \mathrm {C} \ \)を閉曲線,\( \ \mathrm {d}\boldsymbol l \ \)を\( \ \mathrm {C} \ \)上の微小区間ベクトル,\( \ I \ \)を\( \ \mathrm {C} \ \)と鎖交する電流の総量とすると,
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,これをアンペアの周回積分の法則といいます。
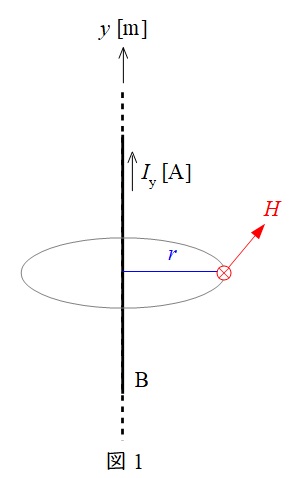
例えば,図1のように無限長直線電流\( \ I_{\mathrm {y}} \ \)が流れているとき,電線から距離\( \ r \ \)の位置での磁界の強さ\( \ H \ \)は,\( \ l=2\pi r \ \)なので,
\[
\begin{eqnarray}
2\pi r H&=&I_{\mathrm {y}} \\[ 5pt ]
H&=&\frac {I_{\mathrm {y}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.\( \ \mathrm {rot} \ \)(回転)
\( \ \mathrm {rot} \ \)の定義は,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol H&=&\left( \frac { \partial H_{\mathrm {z}}}{ \partial y }-\frac { \partial H_{\mathrm {y}}}{ \partial z },\frac { \partial H_{\mathrm {x}}}{ \partial z }-\frac { \partial H_{\mathrm {z}}}{ \partial x },\frac { \partial H_{\mathrm {y}}}{ \partial x }-\frac { \partial H_{\mathrm {x}}}{ \partial y }\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,外積を用いて表すと,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol H &=& \begin{bmatrix} \mathrm {i} & \mathrm {j} & \mathrm {k} \\ \frac { \partial }{ \partial x } & \frac { \partial }{ \partial y } & \frac { \partial }{ \partial z } \\ H_{\mathrm {x}} & H_{\mathrm {y}} & H_{\mathrm {z}} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,こちらの方が覚えやすいと思います。
(\( \ \mathrm {i} \ \),\( \ \mathrm {j} \ \),\( \ \mathrm {k} \ \)は\( \ x \ \)軸,\( \ y \ \)軸,\( \ z \ \)軸の単位ベクトルです)
3.\( \ \mathrm {div} \ \)(発散)
ある微小な立方体の発散量で次式で定義されます。
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol H &=& \frac { \partial H_{\mathrm {x}}}{ \partial x }+\frac { \partial H_{\mathrm {y}}}{ \partial y }+\frac { \partial H_{\mathrm {z}}}{ \partial z } \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ト
\( \ \mathrm {PQ} \ \)に沿った\( \ \boldsymbol H \ \)の線積分は,\( \ \mathrm {PQ}=\Delta x \ \)及び\( \ \boldsymbol H=H_{\mathrm {x}}\left( x,y \right) \ \)であるから,
\[
\begin{eqnarray}
H_{\mathrm {x}}\left( x,y \right) \cdot \Delta x \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
(1)と同様に,閉曲線での磁界の線積分は,
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&H_{\mathrm {x}}\left( x,y \right) \cdot \Delta x +H_{\mathrm {y}}\left( x+\Delta x,y \right) \cdot \Delta y -H_{\mathrm {x}}\left( x,y+\Delta y \right) \cdot \Delta x-H_{\mathrm {y}}\left( x,y \right) \cdot \Delta y \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
①式の右辺は四角形\( \ \mathrm {PQRS} \ \)を通過する電流なので,電流密度\( \ J_{\mathrm {z}} \ \)と四角形\( \ \mathrm {PQRS} \ \)の面積\( \ \Delta S=\Delta x \cdot \Delta y \ \)より,
\[
\begin{eqnarray}
I &=&J_{\mathrm {z}}\cdot \Delta S \\[ 5pt ]
&=&J_{\mathrm {z}}\cdot \Delta x \cdot \Delta y \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ホ
(2)及び(3)の解答式より,
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I \\[ 5pt ]
H_{\mathrm {x}}\left( x,y \right) \cdot \Delta x +H_{\mathrm {y}}\left( x+\Delta x,y \right) \cdot \Delta y -H_{\mathrm {x}}\left( x,y+\Delta y \right) \cdot \Delta x-H_{\mathrm {y}}\left( x,y \right) \cdot \Delta y &=&J_{\mathrm {z}}\cdot \Delta x \cdot \Delta y \\[ 5pt ]
H_{\mathrm {y}}\left( x+\Delta x,y \right) \cdot \Delta y -H_{\mathrm {y}}\left( x,y \right) \cdot \Delta y-H_{\mathrm {x}}\left( x,y+\Delta y \right) \cdot \Delta x +H_{\mathrm {x}}\left( x,y \right) \cdot \Delta x &=&J_{\mathrm {z}}\cdot \Delta x \cdot \Delta y \\[ 5pt ]
\frac {H_{\mathrm {y}}\left( x+\Delta x,y \right) -H_{\mathrm {y}}\left( x,y \right) }{\Delta x}-\frac {H_{\mathrm {x}}\left( x,y+\Delta y \right) -H_{\mathrm {x}}\left( x,y \right) }{\Delta y}&=&J_{\mathrm {z}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
\( \ \Delta x \ \),\( \ \Delta y \ \)ともに\( \ 0 \ \)に近づけると,
\[
\begin{eqnarray}
\frac {\partial H_{\mathrm {y}}}{\partial x}-\frac {\partial H_{\mathrm {x}}}{\partial y}&=&J_{\mathrm {z}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント「2.\( \ \mathrm {rot} \ \)(回転)」の通り,上式は\( \ \mathrm {rot} \boldsymbol H =\boldsymbol J \ \)の\( \ z \ \)方向成分と同じ式になる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん