【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相交流回路に関するに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。ただし,\( \ a \ \)は複素数で\( \ a=e^{\mathrm {j}\frac {2}{3}\pi } \ \)とする。
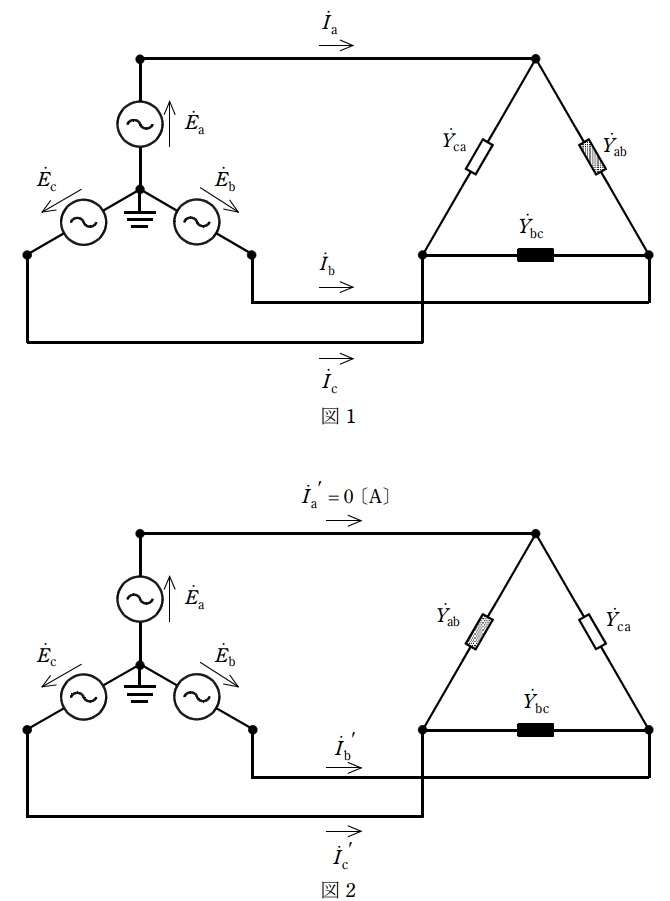
図1と図2に示すように,対称三相交流電源に\( \ \Delta \ \)形不平衡負荷を接続した。図1と図2では,\( \ \Delta \ \)形不平衡負荷のアドミタンス\( \ {\dot Y}_{\mathrm {ab}} \ \)と\( \ {\dot Y}_{\mathrm {ca}} \ \)の配置が入れ替わっている。各相の電圧は\( \ {\dot E}_{\mathrm {a}}=100∠0° \ \mathrm {[V]} \ \)に対し,\( \ {\dot E}_{\mathrm {b}}=a^{2}{\dot E}_{\mathrm {a}} \ \),\( \ {\dot E}_{\mathrm {c}}=a{\dot E}_{\mathrm {a}} \ \)である。図1と図2の\( \ \Delta \ \)形不平衡負荷のベクトル(複素)電力をそれぞれ\( \ {\dot S}_{1} \ \),\( \ {\dot S}_{2} \ \)とする。このとき,以下の結果を得た。
① 図1の線電流\( \ {\dot I}_{\mathrm {a}} \ \)は\( \ {\dot I}_{\mathrm {a}}=10\left( 1-a^{2}\right) \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {b}} \ \)は\( \ {\dot E}_{\mathrm {b}} \ \)と同相,\( \ {\dot I}_{\mathrm {c}} \ \)は\( \ {\dot E}_{\mathrm {a}} \ \)と逆相であった。
② 図2の線電流\( \ {{\dot I}_{\mathrm {a}}}^{\prime } \ \)は\( \ 0 \ \mathrm {[A]} \ \)であった。
③ 図1の\( \ \Delta \ \)形不平衡負荷のベクトル(複素)電力は\( \ {\dot S}_{1} =2000\left( 1-a\right) \ \)(実部は有効電力\( \ \mathrm {[W]} \ \),虚部は無効電力\( \ \mathrm {[var]} \ \))であった。
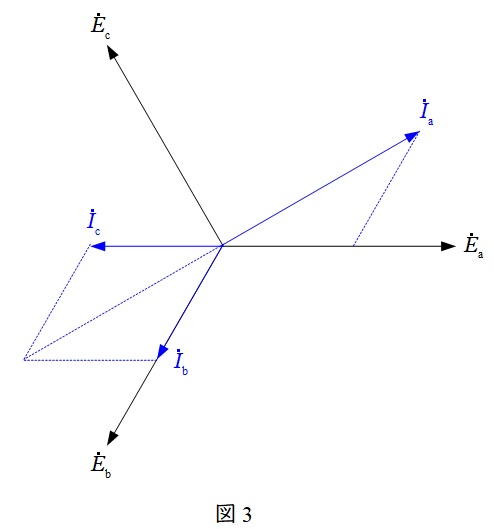
①の結果にキルヒホッフの電流則を適用し,線電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)のベクトル図を描くと,\( \ {\dot I}_{\mathrm {b}} \ \)と\( \ {\dot I}_{\mathrm {c}} \ \)の値は,\( \ \left( {\dot I}_{\mathrm {b}},{\dot I}_{\mathrm {c}}\right) =\fbox { (1) } \ \mathrm {[A]} \ \)となる。
②の結果,\( \ {{\dot I}_{\mathrm {a}}}^{\prime } \ = 0 \ \mathrm {[A]} \ \)より,\( \ {\dot Y}_{\mathrm {ab}}=\fbox { (2) }\times {\dot Y}_{\mathrm {ca}} \ \)となる。ただし,複素数\( \ a \ \)の性質\( \ a^{3}=1 \ \),\( \ 1+a+a^{2}=0 \ \)に注意する。この関係式と図1の線電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \)から\( \ {\dot Y}_{\mathrm {ab}} \ \),\( \ {\dot Y}_{\mathrm {bc}} \ \),\( \ {\dot Y}_{\mathrm {ca}} \ \)が順次求められる。
一方,③の結果を利用すると,アドミタンスの和\( \ {\dot Y}_{\mathrm {ab}}+{\dot Y}_{\mathrm {bc}}+{\dot Y}_{\mathrm {ca}} \ \)の値は,ベクトル(複素)電力\( \ {\dot S}_{1} =\fbox { (3) }\times \left| {\dot E}_{\mathrm {a}}\right| ^{2}\overline {\left( {\dot Y}_{\mathrm {ab}}+{\dot Y}_{\mathrm {bc}}+{\dot Y}_{\mathrm {ca}}\right) } \ \)の式から直接求めることができる。また,②の結果とキルヒホッフの電流則を利用すると図2のベクトル(複素)電力\( \ {\dot S}_{2} \ \)は,\( \ {\dot S}_{2}=\left( \fbox { (4) }\right) \times \overline {{{\dot I}_{\mathrm {c}}}^{\prime }} \ \)と表せる。\( \ {\dot S}_{2} \ \)の式と③の結果を利用すると,\( \ {{\dot I}_{\mathrm {c}}}^{\prime }=\fbox { (5) } \ \mathrm {[A]} \ \)となる。
(注)\( \ \overline {\dot Z} \ \)は複素数\( \ \dot Z \ \)の共役複素数を表す。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 1 &(ロ)& {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {a}} &(ハ)& \left( 20a^{2},-10\right) \\[ 5pt ]
&(ニ)& 3a &(ホ)& a^{2} &(ヘ)& \left( 10a^{2},-20\right) \\[ 5pt ]
&(ト)& 20a &(チ)& {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {b}} &(リ)& 3 \\[ 5pt ]
&(ヌ)& 2a &(ル)& 30a^{2} &(ヲ)& 25a^{2} \\[ 5pt ]
&(ワ)& \left( 10a^{2},-10\right) &(カ)& {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}} &(ヨ)& \sqrt {3} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
不平衡負荷の三相交流に関する問題は1種ならではの問題と言えると思います。1種理論攻略には確実に必要となる分野なので,確実にマスターしましょう。
1.ベクトルオペレータ\(a\)
題意で与えられているベクトルオペレータ\(a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}}\)は,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} &=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} &=& -\frac {1}{2}-\mathrm {j} \frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} &=& 1 \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
\overline {a^{2}} &=& a \\[ 5pt ]
1+a+a^{2} &=& 0
\end{eqnarray}
\]
が成立します。
【解答】
(1)解答:ワ
題意に沿ってベクトル図を描くと図3のようになる。ここで,図1より,\( \ {\dot I}_{\mathrm {b}}∝a^{2} \ \)かつ\( \ {\dot I}_{\mathrm {c}} \ \)は実数であり,三相の合計電流\( \ {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}}=0 \ \)であるから,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} &=& -{\dot I}_{\mathrm {a}} \\[ 5pt ]
&=& -\left[ 10\left( 1-a^{2}\right) \right] \\[ 5pt ]
&=& -10+10a^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ {\dot I}_{\mathrm {b}}=10a^{2} \ \)及び\( \ {\dot I}_{\mathrm {c}}=-10 \ \)と求められる。
(2)解答:ホ
\( \ {{\dot I}_{\mathrm {a}}}^{\prime } \ = 0 \ \mathrm {[A]} \ \)ということは,\( \ {\dot Y}_{\mathrm {ab}} \ \)及び\( \ {\dot Y}_{\mathrm {ca}} \ \)に流れる電流が等しいということなので,
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {ab}}\left( {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {a}}\right) &=& {\dot Y}_{\mathrm {ca}}\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) \\[ 5pt ]
{\dot Y}_{\mathrm {ab}}\left( 100a-100\right) &=& {\dot Y}_{\mathrm {ca}}\left( 100-100a^{2}\right) \\[ 5pt ]
{\dot Y}_{\mathrm {ab}} &=& \frac {1-a^{2}}{a-1}{\dot Y}_{\mathrm {ca}} \\[ 5pt ]
&=& \frac {\left( 1+a\right) \left( 1-a\right) }{a-1}{\dot Y}_{\mathrm {ca}} \\[ 5pt ]
&=& -\left( 1+a\right){\dot Y}_{\mathrm {ca}} \\[ 5pt ]
&=& a^{2}{\dot Y}_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
【補足】
問題文に「\( \ {\dot Y}_{\mathrm {ab}} \ \),\( \ {\dot Y}_{\mathrm {bc}} \ \),\( \ {\dot Y}_{\mathrm {ca}} \ \)が順次求められる。」と書いてあるので,順次求めておきたいと思います。計算の練習になると思うので,時間に余裕があれば行って下さい。
図1より,各アドミタンスに対してキルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {ab}}\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) -{\dot Y}_{\mathrm {ca}}\left( {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {a}}\right) &=& {\dot I}_{\mathrm {a}} \\[ 5pt ]
{\dot Y}_{\mathrm {bc}}\left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) -{\dot Y}_{\mathrm {ab}}\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) &=& {\dot I}_{\mathrm {b}} \\[ 5pt ]
{\dot Y}_{\mathrm {ca}}\left( {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {a}}\right) -{\dot Y}_{\mathrm {bc}}\left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) &=& {\dot I}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となり,各値及び\( \ {\dot Y}_{\mathrm {ab}}=a^{2}{\dot Y}_{\mathrm {ca}} \ \)を代入すると,
\[
\begin{eqnarray}
a^{2}{\dot Y}_{\mathrm {ca}}\left( 100-100a^{2}\right) -{\dot Y}_{\mathrm {ca}}\left( 100a-100\right) &=& 10\left( 1-a^{2}\right) \\[ 5pt ]
{\dot Y}_{\mathrm {bc}}\left( 100a^{2}-100a\right) -a^{2}{\dot Y}_{\mathrm {ca}}\left( 100-100a^{2}\right) &=& 10a^{2} \\[ 5pt ]
{\dot Y}_{\mathrm {ca}}\left( 100a-100\right) -{\dot Y}_{\mathrm {bc}}\left( 100a^{2}-100a\right) &=& -10 \\[ 5pt ]
\end{eqnarray}
\]
となり,各式を整理すると,
\[
\begin{eqnarray}
100\left( a^{2}-2a+1\right){\dot Y}_{\mathrm {ca}}&=& 10\left( 1-a^{2}\right) & ・・・・・・・ ① &\\[ 5pt ]
100a\left(a-1\right) {\dot Y}_{\mathrm {bc}}-100a\left(a-1\right) {\dot Y}_{\mathrm {ca}}&=& 10a^{2} & ・・・・・・・ ②& \\[ 5pt ]
100\left(a-1\right) {\dot Y}_{\mathrm {ca}} -100a\left( a-1\right) {\dot Y}_{\mathrm {bc}} &=& -10 & ・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となる。①より,
\[
\begin{eqnarray}
100\left( a-1\right)^{2}{\dot Y}_{\mathrm {ca}}&=& 10\left( 1-a\right) \left( 1+a\right) \\[ 5pt ]
{\dot Y}_{\mathrm {ca}}&=& \frac {1+a}{10\left( 1-a\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ {\dot Y}_{\mathrm {ab}}=a^{2}{\dot Y}_{\mathrm {ca}} \ \)より,
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {ab}}&=& a^{2}{\dot Y}_{\mathrm {ca}} \\[ 5pt ]
&=& a^{2}\frac {1+a}{10\left( 1-a\right) } \\[ 5pt ]
&=& a^{2}\frac {-a^{2}}{10\left( 1-a\right) } \\[ 5pt ]
&=& \frac {a}{10\left( a-1\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。③より,
\[
\begin{eqnarray}
10\left(a-1\right) {\dot Y}_{\mathrm {ca}} -10a\left( a-1\right) {\dot Y}_{\mathrm {bc}} &=& -1 \\[ 5pt ]
10\left(a-1\right) \cdot \frac {1+a}{10\left( 1-a\right) } -10a\left( a-1\right) {\dot Y}_{\mathrm {bc}} &=& -1 \\[ 5pt ]
-\left( 1+a\right) -10a\left( a-1\right) {\dot Y}_{\mathrm {bc}} &=& -1 \\[ 5pt ]
10a\left( 1-a\right) {\dot Y}_{\mathrm {bc}} &=& a \\[ 5pt ]
{\dot Y}_{\mathrm {bc}} &=& \frac {1}{10\left( 1-a\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
図1より,複素無効電力\( \ {\dot S}_{1} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
{\dot S}_{1}&=& \left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) \overline {{\dot I}_{\mathrm {ab}}}+\left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {bc}}}+\left( {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {a}}\right) \overline {{\dot I}_{\mathrm {ca}}} \\[ 5pt ]
&=& \left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {a}}a^{2}\right) \overline {{\dot Y}_{\mathrm {ab}}\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right)}+\left( {\dot E}_{\mathrm {a}}a^{2}-{\dot E}_{\mathrm {a}}a\right) \overline {{\dot Y}_{\mathrm {bc}}\left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) }+\left( {\dot E}_{\mathrm {a}}a-{\dot E}_{\mathrm {a}}\right) \overline {{\dot Y}_{\mathrm {ca}}\left( {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {a}}\right) } \\[ 5pt ]
&=& {\dot E}_{\mathrm {a}}\left( 1-a^{2}\right) \overline {{\dot Y}_{\mathrm {ab}}{\dot E}_{\mathrm {a}}\left( 1-a^{2}\right)}+{\dot E}_{\mathrm {a}}\left( a^{2}-a\right) \overline {{\dot Y}_{\mathrm {bc}}{\dot E}_{\mathrm {a}}\left( a^{2}-a\right) }+{\dot E}_{\mathrm {a}}\left( a-1\right) \overline {{\dot Y}_{\mathrm {ca}}{\dot E}_{\mathrm {a}}\left( a-1\right) } \\[ 5pt ]
&=& \left| {\dot E}_{\mathrm {a}}\right| ^{2} \left( 1-a^{2}\right) \left( 1-a\right) \overline {{\dot Y}_{\mathrm {ab}}}+\left| {\dot E}_{\mathrm {a}}\right| ^{2} \left( a^{2}-a\right) \left( a-a^{2}\right)\overline {{\dot Y}_{\mathrm {bc}}}+\left| {\dot E}_{\mathrm {a}}\right| ^{2}\left( a-1\right) \left( a^{2}-1\right) \overline {{\dot Y}_{\mathrm {ca}}} \\[ 5pt ]
&=& 3\left| {\dot E}_{\mathrm {a}}\right| ^{2} \overline {{\dot Y}_{\mathrm {ab}}}+3\left| {\dot E}_{\mathrm {a}}\right| ^{2} \overline {{\dot Y}_{\mathrm {bc}}}+3\left| {\dot E}_{\mathrm {a}}\right| ^{2}\overline {{\dot Y}_{\mathrm {ca}}} \\[ 5pt ]
&=& 3\left| {\dot E}_{\mathrm {a}}\right| ^{2} \left( \overline {{\dot Y}_{\mathrm {ab}}}+\overline {{\dot Y}_{\mathrm {bc}}}+\overline {{\dot Y}_{\mathrm {ca}}}\right) \\[ 5pt ]
&=& 3\left| {\dot E}_{\mathrm {a}}\right| ^{2} \left( \overline {{\dot Y}_{\mathrm {ab}}+{\dot Y}_{\mathrm {bc}}+{\dot Y}_{\mathrm {ca}}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:チ
\( \ {{\dot I}_{\mathrm {a}}}^{\prime } = 0 \ \)であるので,\( \ {{\dot I}_{\mathrm {b}}}^{\prime } = -{{\dot I}_{\mathrm {c}}}^{\prime } \ \)となる。したがって,図2におけるベクトル複素電力は,
\[
\begin{eqnarray}
{\dot S}_{2} &=& \left( {\dot E}_{\mathrm {c}}-{\dot E}_{\mathrm {b}}\right) \overline {{\dot I}_{\mathrm {c}}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ト
図1と図2はアドミタンス\( \ {\dot Y}_{\mathrm {ab}} \ \)と\( \ {\dot Y}_{\mathrm {ca}} \ \)の配置が入れ替わっただけなので,ベクトル複素電力の大きさは変わらない。したがって,
\[
\begin{eqnarray}
{\dot S}_{1} &=& {\dot S}_{2} \\[ 5pt ]
2000\left( 1-a\right) &=& \left( 100a-100a^{2}\right) \overline {{\dot I}_{\mathrm {c}}^{\prime }} \\[ 5pt ]
\overline {{\dot I}_{\mathrm {c}}^{\prime }} &=& \frac {20}{a} \\[ 5pt ]
&=& 20a^{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}}^{\prime } &=& 20a \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん