【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,直流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
図のように\( \ R \ \)と\( \ 2R \ \)の\( \ 2 \ \)種類の抵抗を用いた回路がある。まず,全てのスイッチは\( \ 0 \ \)側に接続されているとする。図中の電流\( \ I \ \)は節点\( \ \mathrm {a} \ \)で分流するが,このとき\( \ I_{\mathrm {0}} \ \)は\( \ \fbox { (1) } \ \)。
また,図中の破線より右側の回路の合成抵抗\( \ R_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {a}} &=& \ \fbox { (2) } \ \\[ 5pt ]
\end{eqnarray}
\]
であることから,\( \ I_{\mathrm {1}} \ \)と\( \ I_{\mathrm {0}} \ \)の関係は,
\[
\begin{eqnarray}
I_{\mathrm {1}} &=& \ \fbox { (3) } \ \\[ 5pt ]
\end{eqnarray}
\]
となることがわかる。同様に計算すると,\( \ I_{\mathrm {in}} \ \)と\( \ I_{\mathrm {0}} \ \)の関係は,\( \ I_{\mathrm {in}}= \ \fbox { (4) } \ \)となる。
次に,各スイッチをディジタル信号により制御する。入力された\( \ 3 \ \)ビットの\( \ 2 \ \)進数の最上位ビットから順にスイッチ\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)に対応させ,各ビットの値に応じてスイッチを\( \ 1 \ \)側又は\( \ 0 \ \)側に接続する。例えば,\( \ 2 \ \)進数\( \ \left( 110 \right) _{2} \ \)が入力された場合,スイッチ\( \ \mathrm {A} \ \)を\( \ 1 \ \)側に,スイッチ\( \ \mathrm {B} \ \)を\( \ 1 \ \)側に,スイッチ\( \ \mathrm {C} \ \)を\( \ 0 \ \)側にそれぞれ接続する。スイッチの\( \ 1 \ \)側と\( \ 0 \ \)側はいずれも接地であるから,このときの\( \ I_{\mathrm {out}} \ \)と\( \ I_{\mathrm {0}} \ \)の関係は,\( \ I_{\mathrm {out}}= \ \fbox { (5) } \ \)となる。このことから図の回路は入力されたディジタル信号に応じた電流を出力する回路であることがわかる。

〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 9I_{\mathrm {0}} &(ロ)& 4I_{\mathrm {0}} &(ハ)& 5I_{\mathrm {0}} \\[ 5pt ]
&(ニ)& 8I_{\mathrm {0}} &(ホ)& 3I_{\mathrm {0}} &(ヘ)& R \\[ 5pt ]
&(ト)& Iと等しい &(チ)& 7I_{\mathrm {0}} &(リ)& \frac {1}{2}R \\[ 5pt ]
&(ヌ)& Iの\frac {1}{3}となる &(ル)& Iの\frac {1}{2}となる &(ヲ)& 2I_{\mathrm {0}} \\[ 5pt ]
&(ワ)& 2R &(カ)& 16I_{\mathrm {0}} &(ヨ)& 6I_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
特別難解な公式を使用せず,計算も多くないため,電験一種としては近年稀に見る易しい問題であると思います。
令和2年理論の合格率(64.5%)から考えても,多くの受験生が完答できたのではないかと思います。
計算ミスに注意して確実に解くようにして下さい。
1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時,それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。
①直列
直列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.分圧・分流の法則
①分圧の法則
図1に示した直列回路において,各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ]
V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ]
\end{eqnarray}
\]

②分流の法則
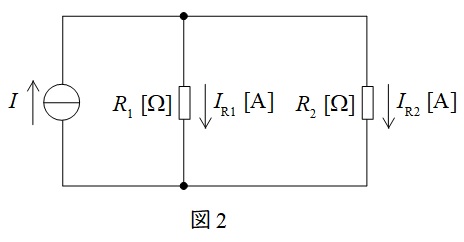
図2に示した並列回路において,各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ]
I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ル
節点\( \ \mathrm {a} \ \)の右側の部分の直列合成抵抗は\( \ 2R \ \)であるから,分流の法則より\( \ I_{\mathrm {0}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {0}}&=&\frac {2R}{2R+2R}I \\[ 5pt ]
&=&\frac {1}{2}I \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ I \ \)の\( \ \displaystyle \frac {1}{2} \ \)となる。
(2)解答:ヘ
破線より右側の回路の合成抵抗\( \ R_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {a}}&=&\frac {2R\cdot 2R}{2R+2R} \\[ 5pt ]
&=&R \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヲ
(2)より,\( \ I \ \)側の合成抵抗は\( \ 2R \ \)であるため,\( \ I_{\mathrm {1}} \ \)側の抵抗\( \ 2R \ \)と値が等しい。したがって,(1)より\( \ I=2I_{\mathrm {0}} \ \)であるから,
\[
\begin{eqnarray}
I_{\mathrm {1}} &=& I \\[ 5pt ]
&=& 2I_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ニ
同様に,\( \ I_{\mathrm {in}} \ \)は右側の回路の合成抵抗\( \ 2R \ \)と\( \ I_{\mathrm {2}} \ \)側の抵抗\( \ 2R \ \)で分流するので,
\[
\begin{eqnarray}
I_{\mathrm {2}} &=& I_{\mathrm {1}}+I \\[ 5pt ]
&=& 2I_{\mathrm {0}}+2I_{\mathrm {0}} \\[ 5pt ]
&=& 4I_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ I_{\mathrm {in}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {in}} &=& I_{\mathrm {2}}+I_{\mathrm {1}}+I \\[ 5pt ]
&=& 4I_{\mathrm {0}}+2I_{\mathrm {0}}+2I_{\mathrm {0}} \\[ 5pt ]
&=& 8I_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
スイッチ\( \ \mathrm {A} \ \)を\( \ 1 \ \)側に,スイッチ\( \ \mathrm {B} \ \)を\( \ 1 \ \)側に,スイッチ\( \ \mathrm {C} \ \)を\( \ 0 \ \)側にそれぞれ接続すると,\( \ I_{\mathrm {out}} \ \)には\( \ 1 \ \)側に接続した電流が流れるので,
\[
\begin{eqnarray}
I_{\mathrm {out}} &=& I_{\mathrm {2}}+I_{\mathrm {1}} \\[ 5pt ]
&=& 4I_{\mathrm {0}}+2I_{\mathrm {0}} \\[ 5pt ]
&=& 6I_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん