《理論》〈電気回路〉[H29:問5] 三相交流回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★★（難しい）

次の文章は，三相交流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

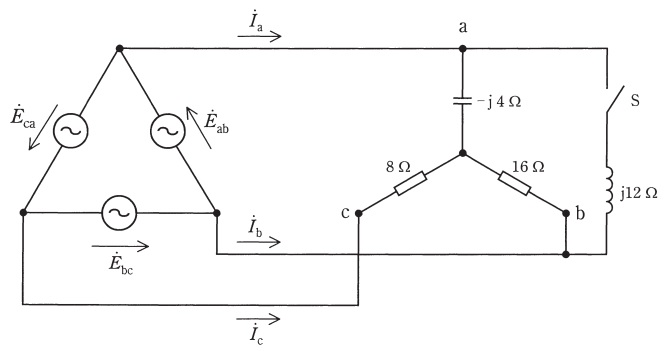
図のように，対称三相交流電源が$ \ \mathrm {Y} \ $形不平衡負荷と$ \ 12 \ \Omega \ $の誘導性リアクタンスからなる回路に接続されている。図の各線間電圧は$ \ {\dot E}_{\mathrm {ab}}=100\angle 0^{\circ } \ [\mathrm {V}] \ $を基準に，$ \ {\dot E}_{\mathrm {bc}}=a^{2}{\dot E}_{\mathrm {ab}} \ $，$ \ {\dot E}_{\mathrm {ca}}=a{\dot E}_{\mathrm {ab}} \ $とする。ただし，$ \ a \ $は複素数で$ \ \displaystyle a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ $である。
いま，スイッチ$ \ \mathrm {S} \ $が開いている状態で線電流を求めると，$ \ {\dot I}_{\mathrm {a}}=\fbox {　（１）　} \ \mathrm {A} \ $，$ \ {\dot I}_{\mathrm {b}}=\fbox {　（２）　} \ \mathrm {A} \ $，$ \ {\dot I}_{\mathrm {c}}=\fbox {　（３）　} \ \mathrm {A} \ $となる。また，負荷で消費される電力は$ \ \fbox {　（４）　} \ \mathrm {W} \ $となる。
次に，スイッチ$ \ \mathrm {S} \ $を閉じ，$ \ 12 \ \Omega \ $の誘導性リアクタンスが端子$ \ \mathrm {a－b} \ $間に並列に接続されたとすると，線電流$ \ {\dot I}_{\mathrm {a}} \ $は$ \ {\dot I}_{\mathrm {a}}=\fbox {　（５）　} \ \mathrm {A} \ $となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　2800　　　&（ロ）&　5.20-\mathrm {j}1.41　　　&（ハ）&　-11.68-\mathrm {j}4.23 \\[ 5pt ] &（ニ）&　-6.71+\mathrm {j}4.23　　　&（ホ）&　13.20-\mathrm {j}9.26　　　&（ヘ）&　13.20-\mathrm {j}0.93 \\[ 5pt ] &（ト）&　5.20+\mathrm {j}6.92　　　&（チ）&　11.68+\mathrm {j}1.41　　　&（リ）&　-6.48-\mathrm {j}3.30 \\[ 5pt ] &（ヌ）&　1350　　　&（ル）&　-5.20-\mathrm {j}6.92　　　&（ヲ）&　-1.52-\mathrm {j}3.30 \\[ 5pt ] &（ワ）&　-6.71+\mathrm {j}3.62　　　&（カ）&　1.52+\mathrm {j}2.70　　　&（ヨ）&　950
\end{eqnarray}
\]

【ワンポイント解説】

回路方程式自体はそれほど難しくありませんが，その後の計算が非常に難解であり，選択肢も絞れない問題です。$\mathrm {Y – \Delta}$変換を用いれば幾分計算は楽になると思います。平成29年の理論の合格点が低かった(80点満点中42点以上)のはこの問題の影響であったと思います。

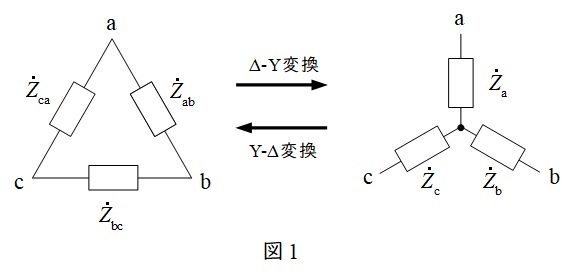
1.不平衡負荷の$ \ \mathrm {\Delta – Y} \ $変換と$ \ \mathrm {Y – \Delta} \ $変換
毎年のように試験で出題されます。一種レベルの受験者であれば，スラスラと思い出せるぐらいにしておきたいところです。
a.$ \ \mathrm {\Delta – Y} \ $変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}} &=& \frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}} &=& \frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] b.$ \ \mathrm {Y – \Delta} \ $変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\]

2.ベクトルオペレータ$ \ a \ $
題意で与えられているベクトルオペレータ$ \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ $は，
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ] &=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ] &=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ] &=& 1 \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　Y⇔Δ回路のインピーダンス変換式

【解答】

(1)解答：ヘ
問題図の回路の負荷を$ \ \mathrm {Y – \Delta} \ $変換すると，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {-\mathrm {j}4\times 16+16\times 8+8\times -\mathrm {j}4}{8} \\[ 5pt ] &=&16-\mathrm {j}12 \ [\Omega ] \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {-\mathrm {j}4\times 16+16\times 8+8\times -\mathrm {j}4}{-\mathrm {j}4} \\[ 5pt ] &=&24+\mathrm {j}32 \ [\Omega ] \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {-\mathrm {j}4\times 16+16\times 8+8\times -\mathrm {j}4}{16} \\[ 5pt ] &=&8-\mathrm {j}6 \ [\Omega ] \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$ \ {\dot Z}_{\mathrm {ab}} \ $，$ \ {\dot Z}_{\mathrm {bc}} \ $，$ \ {\dot Z}_{\mathrm {ca}} \ $に流れる電流を$ \ {\dot I}_{\mathrm {ab}} \ $，$ \ {\dot I}_{\mathrm {bc}} \ $，$ \ {\dot I}_{\mathrm {ca}} \ $とすると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {ab}} &=& \frac {{\dot E}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}} \\[ 5pt ] &=& \frac {100}{16-\mathrm {j}12} \\[ 5pt ] &=& \frac {25}{4-\mathrm {j}3} \\[ 5pt ] &=& \frac {25(4+\mathrm {j}3)}{25} \\[ 5pt ] &=& 4+\mathrm {j}3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
{\dot I}_{\mathrm {bc}}&=&\frac {{\dot E}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {bc}}} \\[ 5pt ] &=& \frac {\displaystyle 100 \times ( -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2})}{24+\mathrm {j}32} \\[ 5pt ] &=& \frac {25 \times ( -1-\mathrm {j}\sqrt {3})}{4\times (3+\mathrm {j}4)} \\[ 5pt ] &=& \frac {25 \times ( -1-\mathrm {j}\sqrt {3})(3-\mathrm {j}4)}{4\times 25} \\[ 5pt ] &=& \frac {-3-4\sqrt {3}+\mathrm {j}(4-3\sqrt {3})}{4} \\[ 5pt ] &≒& -2.482-\mathrm {j}0.299 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
{\dot I}_{\mathrm {ca}} &=& \frac {{\dot E}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] &=& \frac {\displaystyle 100 \times ( -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2})}{8-\mathrm {j}6} \\[ 5pt ] &=& \frac {25 \times ( -1+\mathrm {j}\sqrt {3})}{4-\mathrm {j}3} \\[ 5pt ] &=&\frac {25 \times ( -1+\mathrm {j}\sqrt {3})(4+\mathrm {j}3)}{25} \\[ 5pt ] &=& -4-3\sqrt {3}+\mathrm {j}(-3+4\sqrt {3}) \\[ 5pt ] &≒&-9.196+\mathrm {j}3.928 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。
よって，求める電流$ \ {\dot I}_{\mathrm {a}} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=& {\dot I}_{\mathrm {ab}}-{\dot I}_{\mathrm {ca}} \\[ 5pt ] &=& (4+\mathrm {j}3)-(-9.196+\mathrm {j}3.928) \\[ 5pt ] &=& 13.196-\mathrm {j}0.928 \\[ 5pt ] &≒&13.2-\mathrm {j}0.93 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：リ
(1)より$ \ {\dot I}_{\mathrm {b}} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}} &=& {\dot I}_{\mathrm {bc}}-{\dot I}_{\mathrm {ab}} \\[ 5pt ] &=& (-2.482-\mathrm {j}0.299)-(4+\mathrm {j}3)\\[ 5pt ] &=& -6.482-\mathrm {j}3.299 \\[ 5pt ] &≒&-6.48-\mathrm {j}3.30 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ニ
(1)より$ \ {\dot I}_{\mathrm {c}} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}} &=& {\dot I}_{\mathrm {ca}}-{\dot I}_{\mathrm {bc}} \\[ 5pt ] &=& (-9.196+\mathrm {j}3.928)-(-2.482-\mathrm {j}0.299) \\[ 5pt ] &=& -6.714+\mathrm {j}4.227 \\[ 5pt ] &≒&-6.71+\mathrm {j}4.23 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヌ
負荷で消費される電力$ \ W \ $は，
\[
\begin{eqnarray}
W&=&16\times |{\dot I}_{\mathrm {b}}|^{2}+8\times |{\dot I}_{\mathrm {c}}|^{2} \\[ 5pt ] &=&16\times (6.482^{2}+3.299^{2})+8\times (6.714^{2}+4.227^{2}) \\[ 5pt ] &≒&16\times (42.016+10.833)+8\times (45.078+17.868) \\[ 5pt ] &≒&1349.95 \\[ 5pt ] &≒& 1350 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
スイッチ$ \ \mathrm {S} \ $を閉じた後誘導性リアクタンスに流れる電流を$ \ {\dot I}_{\mathrm {L}} \ $とすると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {L}} &=& \frac {{\dot E}_{\mathrm {ab}}}{\mathrm {j}12} \\[ 5pt ] &=& \frac {100}{\mathrm {j}12} \\[ 5pt ] &≒&-\mathrm {j}8.333 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるから，接続後に流れる線電流$ \ {\dot I}_{\mathrm {a}} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=& 13.196-\mathrm {j}0.928-\mathrm {j}8.333 \\[ 5pt ] &=& 13.196-\mathrm {j}9.261 \\[ 5pt ] &≒& 13.2-\mathrm {j}9.26 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。